Shreyas Sundaram
Robust Information Selection for Hypothesis Testing with Misclassification Penalties
Feb 21, 2025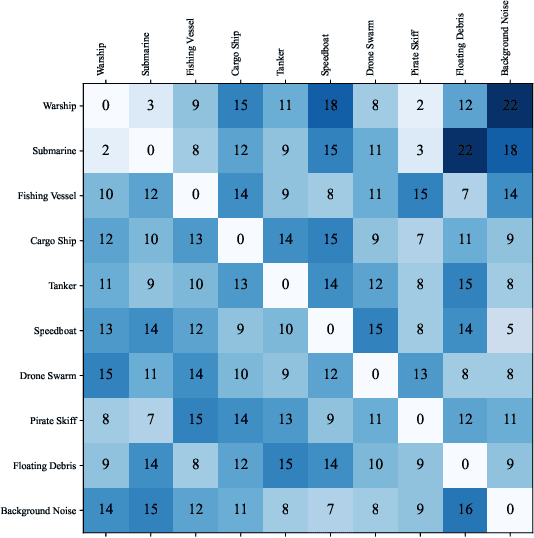
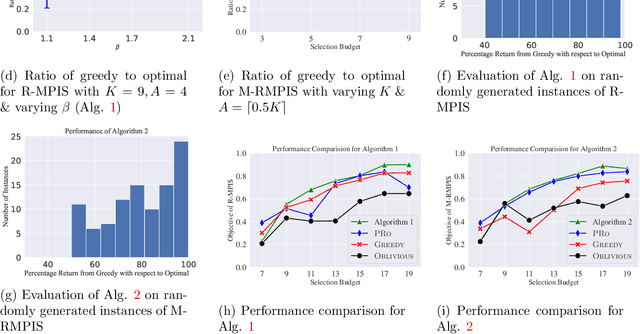
Abstract:We study the problem of robust information selection for a Bayesian hypothesis testing / classification task, where the goal is to identify the true state of the world from a finite set of hypotheses based on observations from the selected information sources. We introduce a novel misclassification penalty framework, which enables non-uniform treatment of different misclassification events. Extending the classical subset selection framework, we study the problem of selecting a subset of sources that minimize the maximum penalty of misclassification under a limited budget, despite deletions or failures of a subset of the selected sources. We characterize the curvature properties of the objective function and propose an efficient greedy algorithm with performance guarantees. Next, we highlight certain limitations of optimizing for the maximum penalty metric and propose a submodular surrogate metric to guide the selection of the information set. We propose a greedy algorithm with near-optimality guarantees for optimizing the surrogate metric. Finally, we empirically demonstrate the performance of our proposed algorithms in several instances of the information set selection problem.
Classification with a Network of Partially Informative Agents: Enabling Wise Crowds from Individually Myopic Classifiers
Sep 30, 2024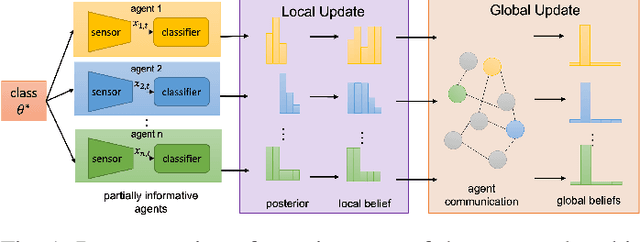
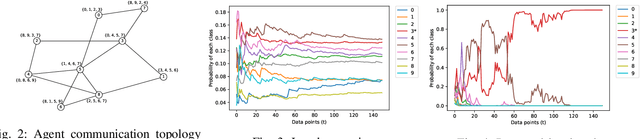
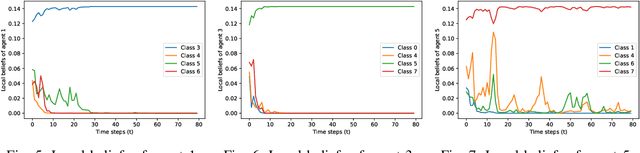
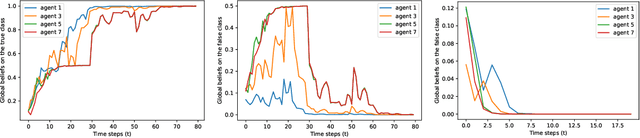
Abstract:We consider the problem of classification with a (peer-to-peer) network of heterogeneous and partially informative agents, each receiving local data generated by an underlying true class, and equipped with a classifier that can only distinguish between a subset of the entire set of classes. We propose an iterative algorithm that uses the posterior probabilities of the local classifier and recursively updates each agent's local belief on all the possible classes, based on its local signals and belief information from its neighbors. We then adopt a novel distributed min-rule to update each agent's global belief and enable learning of the true class for all agents. We show that under certain assumptions, the beliefs on the true class converge to one asymptotically almost surely. We provide the asymptotic convergence rate, and demonstrate the performance of our algorithm through simulation with image data and experimented with random forest classifiers and MobileNet.
Submodular Information Selection for Hypothesis Testing with Misclassification Penalties
May 17, 2024Abstract:We consider the problem of selecting an optimal subset of information sources for a hypothesis testing/classification task where the goal is to identify the true state of the world from a finite set of hypotheses, based on finite observation samples from the sources. In order to characterize the learning performance, we propose a misclassification penalty framework, which enables non-uniform treatment of different misclassification errors. In a centralized Bayesian learning setting, we study two variants of the subset selection problem: (i) selecting a minimum cost information set to ensure that the maximum penalty of misclassifying the true hypothesis remains bounded and (ii) selecting an optimal information set under a limited budget to minimize the maximum penalty of misclassifying the true hypothesis. Under mild assumptions, we prove that the objective (or constraints) of these combinatorial optimization problems are weak (or approximate) submodular, and establish high-probability performance guarantees for greedy algorithms. Further, we propose an alternate metric for information set selection which is based on the total penalty of misclassification. We prove that this metric is submodular and establish near-optimal guarantees for the greedy algorithms for both the information set selection problems. Finally, we present numerical simulations to validate our theoretical results over several randomly generated instances.
C3D: Cascade Control with Change Point Detection and Deep Koopman Learning for Autonomous Surface Vehicles
Mar 14, 2024Abstract:In this paper, we discuss the development and deployment of a robust autonomous system capable of performing various tasks in the maritime domain under unknown dynamic conditions. We investigate a data-driven approach based on modular design for ease of transfer of autonomy across different maritime surface vessel platforms. The data-driven approach alleviates issues related to a priori identification of system models that may become deficient under evolving system behaviors or shifting, unanticipated, environmental influences. Our proposed learning-based platform comprises a deep Koopman system model and a change point detector that provides guidance on domain shifts prompting relearning under severe exogenous and endogenous perturbations. Motion control of the autonomous system is achieved via an optimal controller design. The Koopman linearized model naturally lends itself to a linear-quadratic regulator (LQR) control design. We propose the C3D control architecture Cascade Control with Change Point Detection and Deep Koopman Learning. The framework is verified in station keeping task on an ASV in both simulation and real experiments. The approach achieved at least 13.9 percent improvement in mean distance error in all test cases compared to the methods that do not consider system changes.
Online Change Points Detection for Linear Dynamical Systems with Finite Sample Guarantees
Nov 30, 2023Abstract:The problem of online change point detection is to detect abrupt changes in properties of time series, ideally as soon as possible after those changes occur. Existing work on online change point detection either assumes i.i.d data, focuses on asymptotic analysis, does not present theoretical guarantees on the trade-off between detection accuracy and detection delay, or is only suitable for detecting single change points. In this work, we study the online change point detection problem for linear dynamical systems with unknown dynamics, where the data exhibits temporal correlations and the system could have multiple change points. We develop a data-dependent threshold that can be used in our test that allows one to achieve a pre-specified upper bound on the probability of making a false alarm. We further provide a finite-sample-based bound for the probability of detecting a change point. Our bound demonstrates how parameters used in our algorithm affect the detection probability and delay, and provides guidance on the minimum required time between changes to guarantee detection.
Robust Online Covariance and Sparse Precision Estimation Under Arbitrary Data Corruption
Sep 16, 2023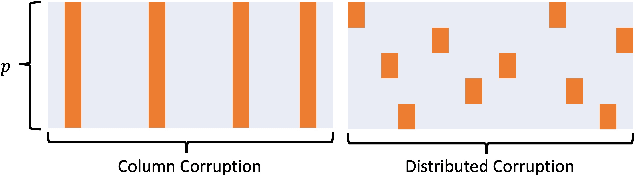
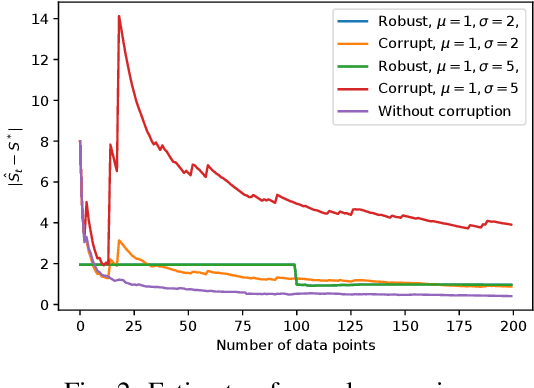
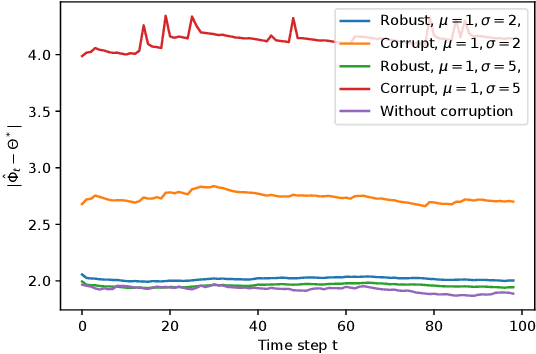
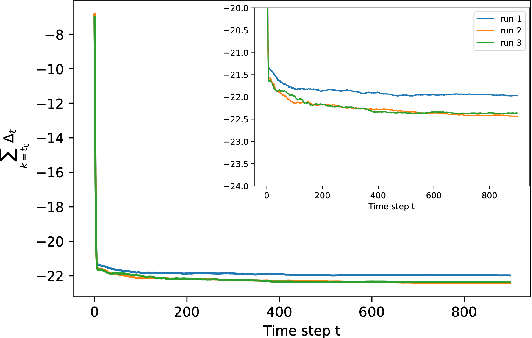
Abstract:Gaussian graphical models are widely used to represent correlations among entities but remain vulnerable to data corruption. In this work, we introduce a modified trimmed-inner-product algorithm to robustly estimate the covariance in an online scenario even in the presence of arbitrary and adversarial data attacks. At each time step, data points, drawn nominally independently and identically from a multivariate Gaussian distribution, arrive. However, a certain fraction of these points may have been arbitrarily corrupted. We propose an online algorithm to estimate the sparse inverse covariance (i.e., precision) matrix despite this corruption. We provide the error-bound and convergence properties of the estimates to the true precision matrix under our algorithms.
Learning Linearized Models from Nonlinear Systems with Finite Data
Sep 15, 2023


Abstract:Identifying a linear system model from data has wide applications in control theory. The existing work on finite sample analysis for linear system identification typically uses data from a single system trajectory under i.i.d random inputs, and assumes that the underlying dynamics is truly linear. In contrast, we consider the problem of identifying a linearized model when the true underlying dynamics is nonlinear. We provide a multiple trajectories-based deterministic data acquisition algorithm followed by a regularized least squares algorithm, and provide a finite sample error bound on the learned linearized dynamics. Our error bound demonstrates a trade-off between the error due to nonlinearity and the error due to noise, and shows that one can learn the linearized dynamics with arbitrarily small error given sufficiently many samples. We validate our results through experiments, where we also show the potential insufficiency of linear system identification using a single trajectory with i.i.d random inputs, when nonlinearity does exist.
Deep Reinforcement Learning Based Framework for Mobile Energy Disseminator Dispatching to Charge On-the-Road Electric Vehicles
Aug 29, 2023Abstract:The exponential growth of electric vehicles (EVs) presents novel challenges in preserving battery health and in addressing the persistent problem of vehicle range anxiety. To address these concerns, wireless charging, particularly, Mobile Energy Disseminators (MEDs) have emerged as a promising solution. The MED is mounted behind a large vehicle and charges all participating EVs within a radius upstream of it. Unfortuantely, during such V2V charging, the MED and EVs inadvertently form platoons, thereby occupying multiple lanes and impairing overall corridor travel efficiency. In addition, constrained budgets for MED deployment necessitate the development of an effective dispatching strategy to determine optimal timing and locations for introducing the MEDs into traffic. This paper proposes a deep reinforcement learning (DRL) based methodology to develop a vehicle dispatching framework. In the first component of the framework, we develop a realistic reinforcement learning environment termed "ChargingEnv" which incorporates a reliable charging simulation system that accounts for common practical issues in wireless charging deployment, specifically, the charging panel misalignment. The second component, the Proximal-Policy Optimization (PPO) agent, is trained to control MED dispatching through continuous interactions with ChargingEnv. Numerical experiments were carried out to demonstrate the demonstrate the efficacy of the proposed MED deployment decision processor. The experiment results suggest that the proposed model can significantly enhance EV travel range while efficiently deploying a optimal number of MEDs. The proposed model is found to be not only practical in its applicability but also has promises of real-world effectiveness. The proposed model can help travelers to maximize EV range and help road agencies or private-sector vendors to manage the deployment of MEDs efficiently.
Multi-Robot Persistent Monitoring: Minimizing Latency and Number of Robots with Recharging Constraints
Mar 15, 2023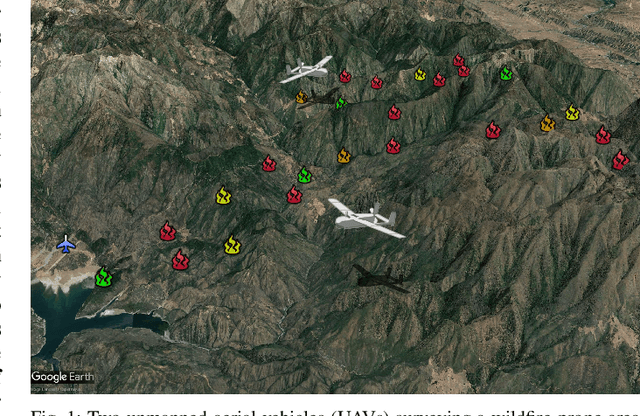
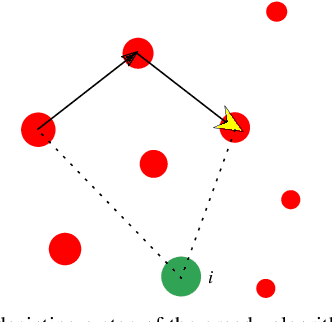
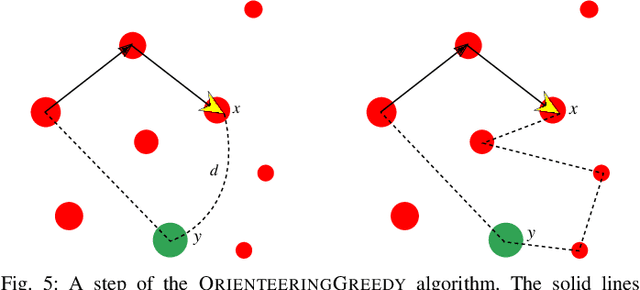
Abstract:In this paper we study multi-robot path planning for persistent monitoring tasks. We consider the case where robots have a limited battery capacity with a discharge time $D$. We represent the areas to be monitored as the vertices of a weighted graph. For each vertex, there is a constraint on the maximum allowable time between robot visits, called the latency. The objective is to find the minimum number of robots that can satisfy these latency constraints while also ensuring that the robots periodically charge at a recharging depot. The decision version of this problem is known to be PSPACE-complete. We present a $O(\frac{\log D}{\log \log D}\log \rho)$ approximation algorithm for the problem where $\rho$ is the ratio of the maximum and the minimum latency constraints. We also present an orienteering based heuristic to solve the problem and show empirically that it typically provides higher quality solutions than the approximation algorithm. We extend our results to provide an algorithm for the problem of minimizing the maximum weighted latency given a fixed number of robots. We evaluate our algorithms on large problem instances in a patrolling scenario and in a wildfire monitoring application. We also compare the algorithms with an existing solver on benchmark instances.
On the Benefits of Leveraging Structural Information in Planning Over the Learned Model
Mar 15, 2023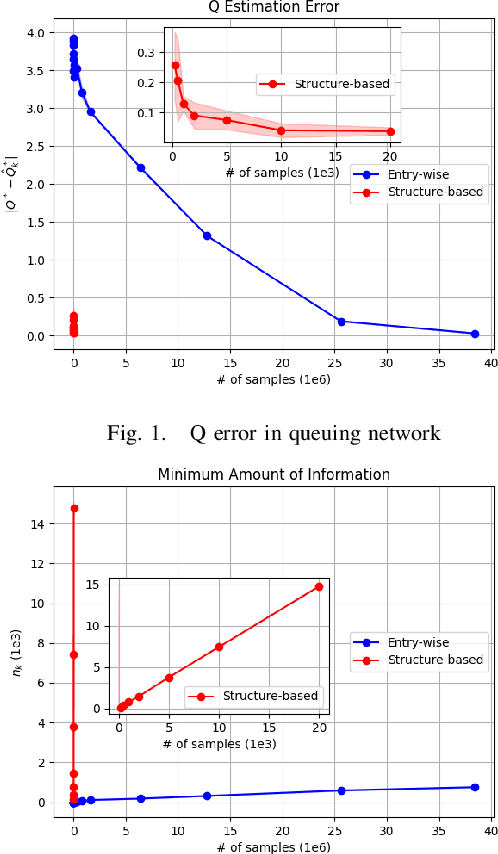
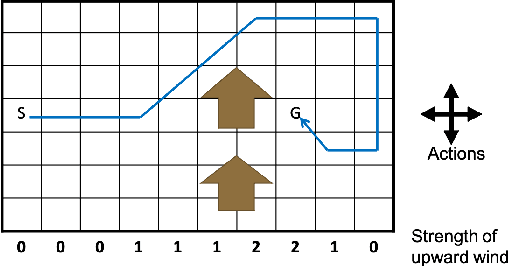
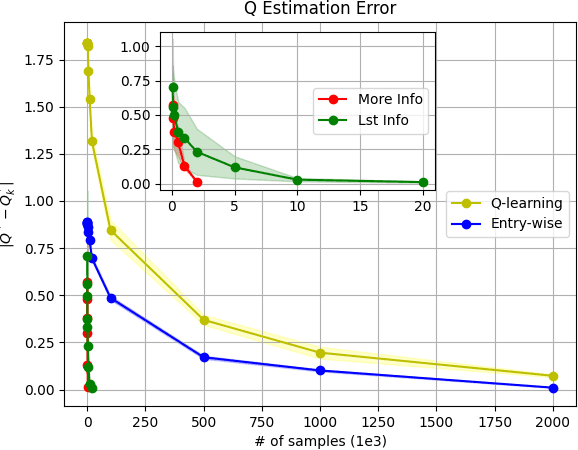
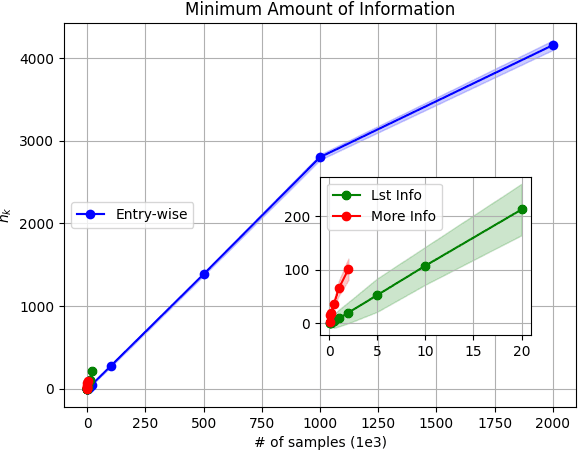
Abstract:Model-based Reinforcement Learning (RL) integrates learning and planning and has received increasing attention in recent years. However, learning the model can incur a significant cost (in terms of sample complexity), due to the need to obtain a sufficient number of samples for each state-action pair. In this paper, we investigate the benefits of leveraging structural information about the system in terms of reducing sample complexity. Specifically, we consider the setting where the transition probability matrix is a known function of a number of structural parameters, whose values are initially unknown. We then consider the problem of estimating those parameters based on the interactions with the environment. We characterize the difference between the Q estimates and the optimal Q value as a function of the number of samples. Our analysis shows that there can be a significant saving in sample complexity by leveraging structural information about the model. We illustrate the findings by considering several problems including controlling a queuing system with heterogeneous servers, and seeking an optimal path in a stochastic windy gridworld.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge