Robust Online Covariance and Sparse Precision Estimation Under Arbitrary Data Corruption
Paper and Code
Sep 16, 2023
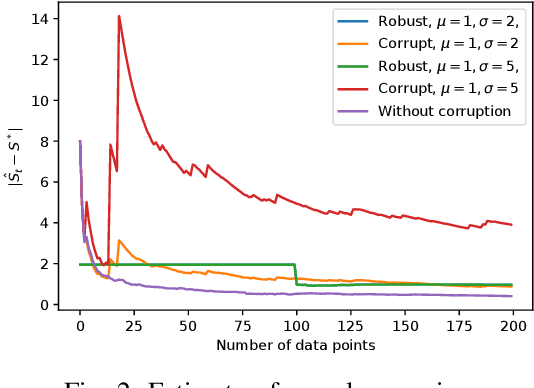
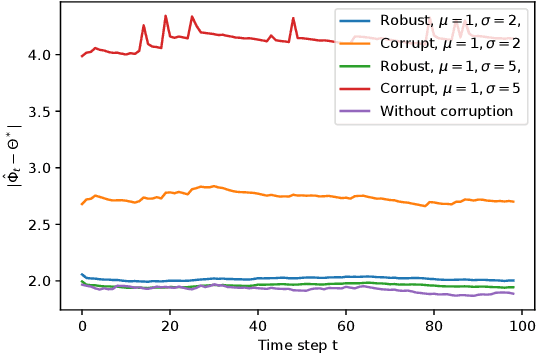
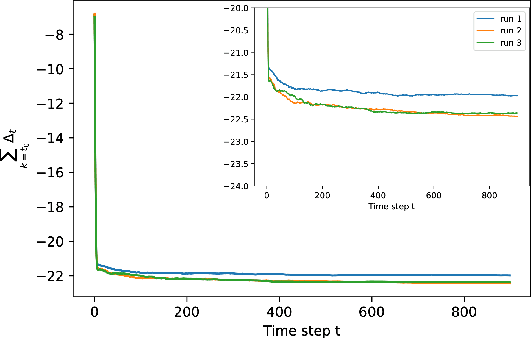
Gaussian graphical models are widely used to represent correlations among entities but remain vulnerable to data corruption. In this work, we introduce a modified trimmed-inner-product algorithm to robustly estimate the covariance in an online scenario even in the presence of arbitrary and adversarial data attacks. At each time step, data points, drawn nominally independently and identically from a multivariate Gaussian distribution, arrive. However, a certain fraction of these points may have been arbitrarily corrupted. We propose an online algorithm to estimate the sparse inverse covariance (i.e., precision) matrix despite this corruption. We provide the error-bound and convergence properties of the estimates to the true precision matrix under our algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge