Classification with a Network of Partially Informative Agents: Enabling Wise Crowds from Individually Myopic Classifiers

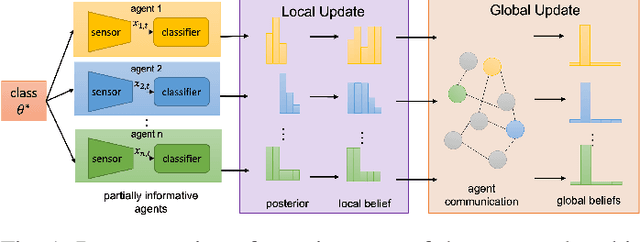
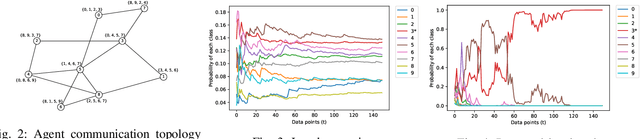
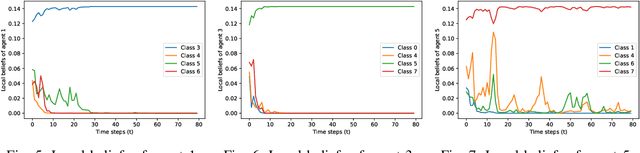
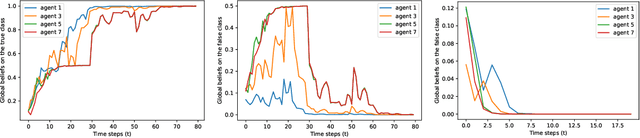
We consider the problem of classification with a (peer-to-peer) network of heterogeneous and partially informative agents, each receiving local data generated by an underlying true class, and equipped with a classifier that can only distinguish between a subset of the entire set of classes. We propose an iterative algorithm that uses the posterior probabilities of the local classifier and recursively updates each agent's local belief on all the possible classes, based on its local signals and belief information from its neighbors. We then adopt a novel distributed min-rule to update each agent's global belief and enable learning of the true class for all agents. We show that under certain assumptions, the beliefs on the true class converge to one asymptotically almost surely. We provide the asymptotic convergence rate, and demonstrate the performance of our algorithm through simulation with image data and experimented with random forest classifiers and MobileNet.

Robust Online Covariance and Sparse Precision Estimation Under Arbitrary Data Corruption

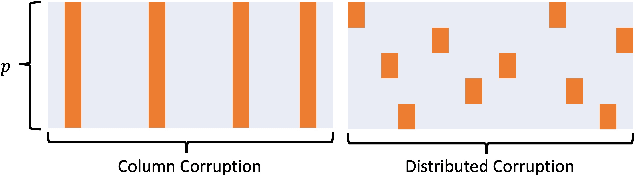
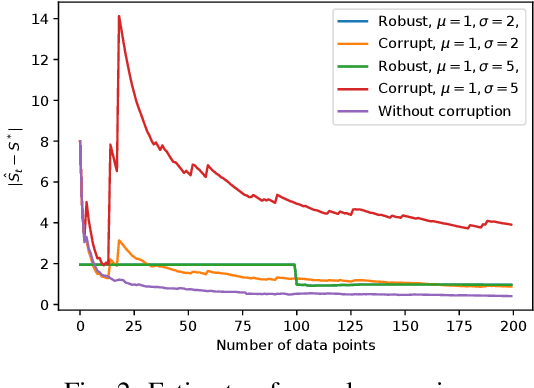
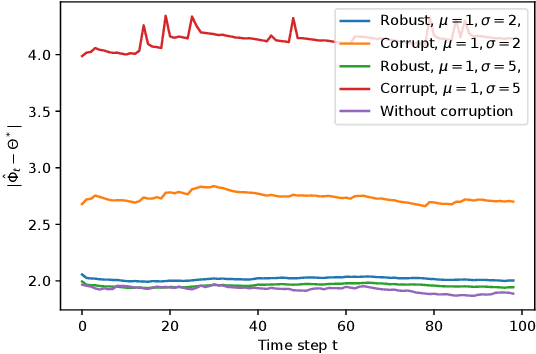
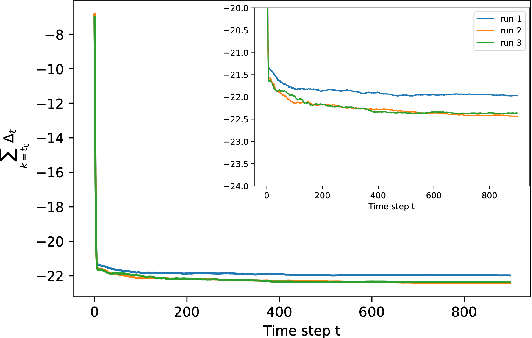
Gaussian graphical models are widely used to represent correlations among entities but remain vulnerable to data corruption. In this work, we introduce a modified trimmed-inner-product algorithm to robustly estimate the covariance in an online scenario even in the presence of arbitrary and adversarial data attacks. At each time step, data points, drawn nominally independently and identically from a multivariate Gaussian distribution, arrive. However, a certain fraction of these points may have been arbitrarily corrupted. We propose an online algorithm to estimate the sparse inverse covariance (i.e., precision) matrix despite this corruption. We provide the error-bound and convergence properties of the estimates to the true precision matrix under our algorithms.

Robust Online and Distributed Mean Estimation Under Adversarial Data Corruption

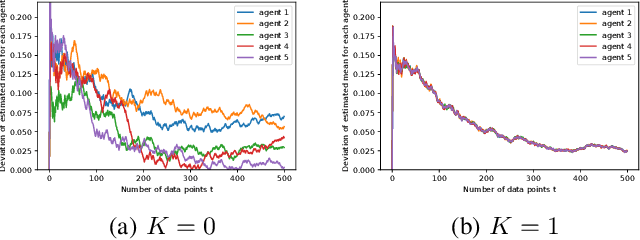
We study robust mean estimation in an online and distributed scenario in the presence of adversarial data attacks. At each time step, each agent in a network receives a potentially corrupted data point, where the data points were originally independent and identically distributed samples of a random variable. We propose online and distributed algorithms for all agents to asymptotically estimate the mean. We provide the error-bound and the convergence properties of the estimates to the true mean under our algorithms. Based on the network topology, we further evaluate each agent's trade-off in convergence rate between incorporating data from neighbors and learning with only local observations.

Distributed Estimation of Sparse Inverse Covariances

Learning the relationships between various entities from time-series data is essential in many applications. Gaussian graphical models have been studied to infer these relationships. However, existing algorithms process data in a batch at a central location, limiting their applications in scenarios where data is gathered by different agents. In this paper, we propose a distributed sparse inverse covariance algorithm to learn the network structure (i.e., dependencies among observed entities) in real-time from data collected by distributed agents. Our approach is built on an online graphical alternating minimization algorithm, augmented with a consensus term that allows agents to learn the desired structure cooperatively. We allow the system designer to select the number of communication rounds and optimization steps per data point. We characterize the rate of convergence of our algorithm and provide simulations on synthetic datasets.