Classification with a Network of Partially Informative Agents: Enabling Wise Crowds from Individually Myopic Classifiers
Paper and Code
Sep 30, 2024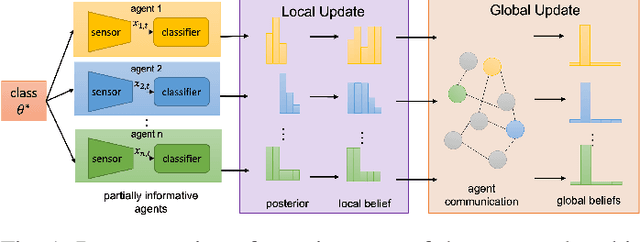
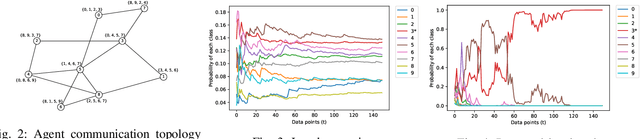
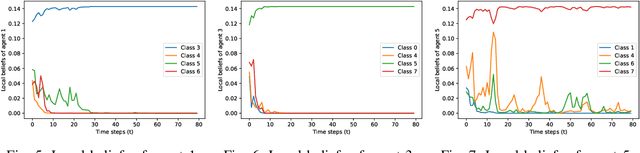
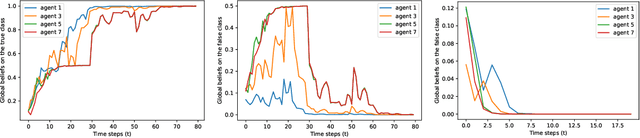
We consider the problem of classification with a (peer-to-peer) network of heterogeneous and partially informative agents, each receiving local data generated by an underlying true class, and equipped with a classifier that can only distinguish between a subset of the entire set of classes. We propose an iterative algorithm that uses the posterior probabilities of the local classifier and recursively updates each agent's local belief on all the possible classes, based on its local signals and belief information from its neighbors. We then adopt a novel distributed min-rule to update each agent's global belief and enable learning of the true class for all agents. We show that under certain assumptions, the beliefs on the true class converge to one asymptotically almost surely. We provide the asymptotic convergence rate, and demonstrate the performance of our algorithm through simulation with image data and experimented with random forest classifiers and MobileNet.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge