Robust Online and Distributed Mean Estimation Under Adversarial Data Corruption
Paper and Code
Sep 17, 2022

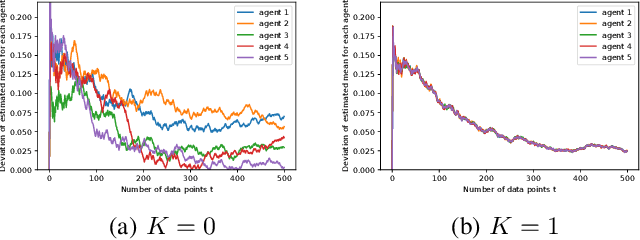
We study robust mean estimation in an online and distributed scenario in the presence of adversarial data attacks. At each time step, each agent in a network receives a potentially corrupted data point, where the data points were originally independent and identically distributed samples of a random variable. We propose online and distributed algorithms for all agents to asymptotically estimate the mean. We provide the error-bound and the convergence properties of the estimates to the true mean under our algorithms. Based on the network topology, we further evaluate each agent's trade-off in convergence rate between incorporating data from neighbors and learning with only local observations.
* 8 pages, 5 figures, 61st IEEE Conference on Decision and Control
(CDC)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge