Online Change Points Detection for Linear Dynamical Systems with Finite Sample Guarantees

The problem of online change point detection is to detect abrupt changes in properties of time series, ideally as soon as possible after those changes occur. Existing work on online change point detection either assumes i.i.d data, focuses on asymptotic analysis, does not present theoretical guarantees on the trade-off between detection accuracy and detection delay, or is only suitable for detecting single change points. In this work, we study the online change point detection problem for linear dynamical systems with unknown dynamics, where the data exhibits temporal correlations and the system could have multiple change points. We develop a data-dependent threshold that can be used in our test that allows one to achieve a pre-specified upper bound on the probability of making a false alarm. We further provide a finite-sample-based bound for the probability of detecting a change point. Our bound demonstrates how parameters used in our algorithm affect the detection probability and delay, and provides guidance on the minimum required time between changes to guarantee detection.

Learning Linearized Models from Nonlinear Systems with Finite Data

Identifying a linear system model from data has wide applications in control theory. The existing work on finite sample analysis for linear system identification typically uses data from a single system trajectory under i.i.d random inputs, and assumes that the underlying dynamics is truly linear. In contrast, we consider the problem of identifying a linearized model when the true underlying dynamics is nonlinear. We provide a multiple trajectories-based deterministic data acquisition algorithm followed by a regularized least squares algorithm, and provide a finite sample error bound on the learned linearized dynamics. Our error bound demonstrates a trade-off between the error due to nonlinearity and the error due to noise, and shows that one can learn the linearized dynamics with arbitrarily small error given sufficiently many samples. We validate our results through experiments, where we also show the potential insufficiency of linear system identification using a single trajectory with i.i.d random inputs, when nonlinearity does exist.

Learning Dynamical Systems by Leveraging Data from Similar Systems

We consider the problem of learning the dynamics of a linear system when one has access to data generated by an auxiliary system that shares similar (but not identical) dynamics, in addition to data from the true system. We use a weighted least squares approach, and provide a finite sample error bound of the learned model as a function of the number of samples and various system parameters from the two systems as well as the weight assigned to the auxiliary data. We show that the auxiliary data can help to reduce the intrinsic system identification error due to noise, at the price of adding a portion of error that is due to the differences between the two system models. We further provide a data-dependent bound that is computable when some prior knowledge about the systems is available. This bound can also be used to determine the weight that should be assigned to the auxiliary data during the model training stage.

Finite Sample Guarantees for Distributed Online Parameter Estimation with Communication Costs

We study the problem of estimating an unknown parameter in a distributed and online manner. Existing work on distributed online learning typically either focuses on asymptotic analysis, or provides bounds on regret. However, these results may not directly translate into bounds on the error of the learned model after a finite number of time-steps. In this paper, we propose a distributed online estimation algorithm which enables each agent in a network to improve its estimation accuracy by communicating with neighbors. We provide non-asymptotic bounds on the estimation error, leveraging the statistical properties of the underlying model. Our analysis demonstrates a trade-off between estimation error and communication costs. Further, our analysis allows us to determine a time at which the communication can be stopped (due to the costs associated with communications), while meeting a desired estimation accuracy. We also provide a numerical example to validate our results.

Identifying the Dynamics of a System by Leveraging Data from Similar Systems

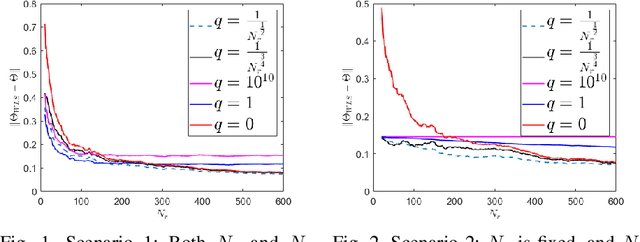
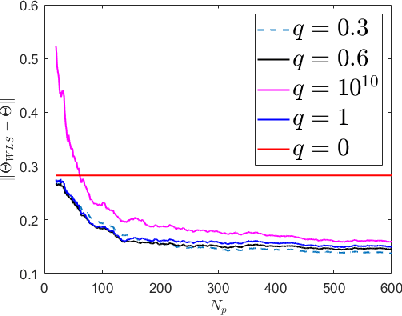
We study the problem of identifying the dynamics of a linear system when one has access to samples generated by a similar (but not identical) system, in addition to data from the true system. We use a weighted least squares approach and provide finite sample performance guarantees on the quality of the identified dynamics. Our results show that one can effectively use the auxiliary data generated by the similar system to reduce the estimation error due to the process noise, at the cost of adding a portion of error that is due to intrinsic differences in the models of the true and auxiliary systems. We also provide numerical experiments to validate our theoretical results. Our analysis can be applied to a variety of important settings. For example, if the system dynamics change at some point in time (e.g., due to a fault), how should one leverage data from the prior system in order to learn the dynamics of the new system? As another example, if there is abundant data available from a simulated (but imperfect) model of the true system, how should one weight that data compared to the real data from the system? Our analysis provides insights into the answers to these questions.

Learning the Dynamics of Autonomous Linear Systems From Multiple Trajectories

We consider the problem of learning the dynamics of autonomous linear systems (i.e., systems that are not affected by external control inputs) from observations of multiple trajectories of those systems, with finite sample guarantees. Existing results on learning rate and consistency of autonomous linear system identification rely on observations of steady state behaviors from a single long trajectory, and are not applicable to unstable systems. In contrast, we consider the scenario of learning system dynamics based on multiple short trajectories, where there are no easily observed steady state behaviors. We provide a finite sample analysis, which shows that the dynamics can be learned at a rate $\mathcal{O}(\frac{1}{\sqrt{N}})$ for both stable and unstable systems, where $N$ is the number of trajectories, when the initial state of the system has zero mean (which is a common assumption in the existing literature). We further generalize our result to the case where the initial state has non-zero mean. We show that one can adjust the length of the trajectories to achieve a learning rate of $\mathcal{O}(\sqrt{\frac{\log{N}}{N})}$ for strictly stable systems and a learning rate of $\mathcal{O}(\frac{(\log{N})^d}{\sqrt{N}})$ for marginally stable systems, where $d$ is some constant.