Identifying the Dynamics of a System by Leveraging Data from Similar Systems
Paper and Code
Apr 11, 2022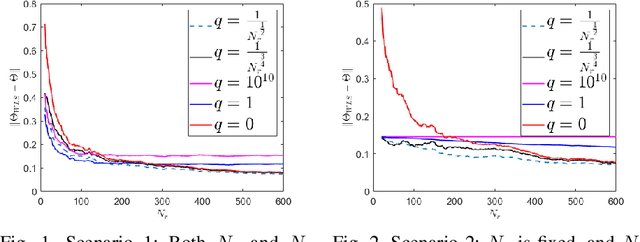
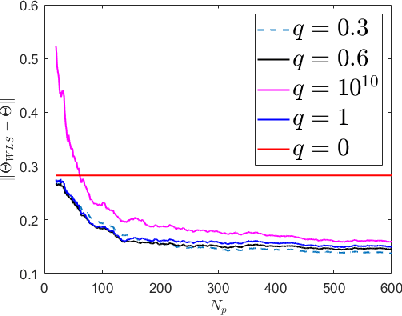
We study the problem of identifying the dynamics of a linear system when one has access to samples generated by a similar (but not identical) system, in addition to data from the true system. We use a weighted least squares approach and provide finite sample performance guarantees on the quality of the identified dynamics. Our results show that one can effectively use the auxiliary data generated by the similar system to reduce the estimation error due to the process noise, at the cost of adding a portion of error that is due to intrinsic differences in the models of the true and auxiliary systems. We also provide numerical experiments to validate our theoretical results. Our analysis can be applied to a variety of important settings. For example, if the system dynamics change at some point in time (e.g., due to a fault), how should one leverage data from the prior system in order to learn the dynamics of the new system? As another example, if there is abundant data available from a simulated (but imperfect) model of the true system, how should one weight that data compared to the real data from the system? Our analysis provides insights into the answers to these questions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge