Deceptive Planning for Resource Allocation

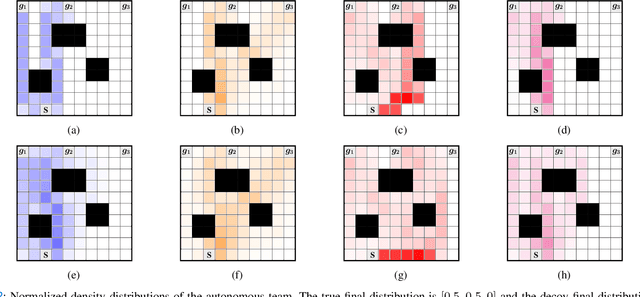
We consider a team of autonomous agents that navigate in an adversarial environment and aim to achieve a task by allocating their resources over a set of target locations. The adversaries in the environment observe the autonomous team's behavior to infer their objective and counter-allocate their own resources to the target locations. In this setting, we develop strategies for controlling the density of the autonomous team so that they can deceive the adversaries regarding their objective while achieving the desired final resource allocation. We first develop a prediction algorithm, based on the principle of maximum entropy, to express the team's behavior expected by the adversaries. Then, by measuring the deceptiveness via Kullback-Leibler divergence, we develop convex optimization-based planning algorithms that deceives adversaries by either exaggerating the behavior towards a decoy allocation strategy or creating ambiguity regarding the final allocation strategy. Finally, we illustrate the performance of the proposed algorithms through numerical simulations.

No-Regret Learning in Dynamic Stackelberg Games

In a Stackelberg game, a leader commits to a randomized strategy, and a follower chooses their best strategy in response. We consider an extension of a standard Stackelberg game, called a discrete-time dynamic Stackelberg game, that has an underlying state space that affects the leader's rewards and available strategies and evolves in a Markovian manner depending on both the leader and follower's selected strategies. Although standard Stackelberg games have been utilized to improve scheduling in security domains, their deployment is often limited by requiring complete information of the follower's utility function. In contrast, we consider scenarios where the follower's utility function is unknown to the leader; however, it can be linearly parameterized. Our objective then is to provide an algorithm that prescribes a randomized strategy to the leader at each step of the game based on observations of how the follower responded in previous steps. We design a no-regret learning algorithm that, with high probability, achieves a regret bound (when compared to the best policy in hindsight) which is sublinear in the number of time steps; the degree of sublinearity depends on the number of features representing the follower's utility function. The regret of the proposed learning algorithm is independent of the size of the state space and polynomial in the rest of the parameters of the game. We show that the proposed learning algorithm outperforms existing model-free reinforcement learning approaches.

On the Detection of Markov Decision Processes

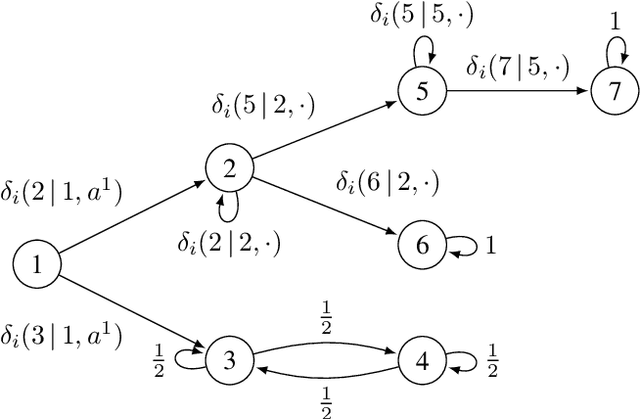
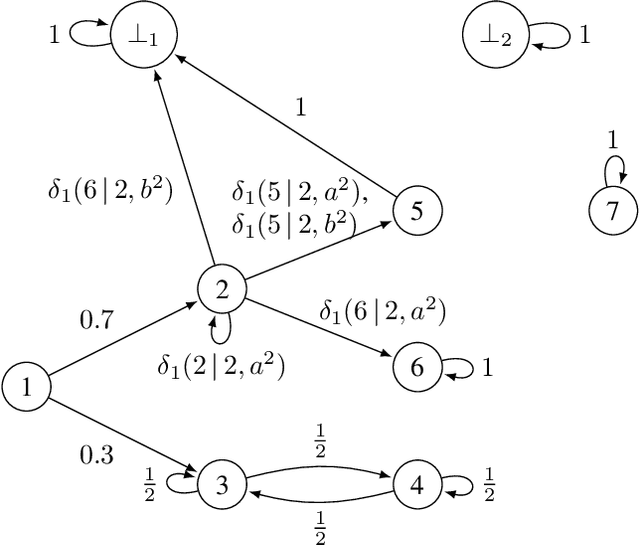
We study the detection problem for a finite set of Markov decision processes (MDPs) where the MDPs have the same state and action spaces but possibly different probabilistic transition functions. Any one of these MDPs could be the model for some underlying controlled stochastic process, but it is unknown a priori which MDP is the ground truth. We investigate whether it is possible to asymptotically detect the ground truth MDP model perfectly based on a single observed history (state-action sequence). Since the generation of histories depends on the policy adopted to control the MDPs, we discuss the existence and synthesis of policies that allow for perfect detection. We start with the case of two MDPs and establish a necessary and sufficient condition for the existence of policies that lead to perfect detection. Based on this condition, we then develop an algorithm that efficiently (in time polynomial in the size of the MDPs) determines the existence of policies and synthesizes one when they exist. We further extend the results to the more general case where there are more than two MDPs in the candidate set, and we develop a policy synthesis algorithm based on the breadth-first search and recursion. We demonstrate the effectiveness of our algorithms through numerical examples.

Deceptive Decision-Making Under Uncertainty

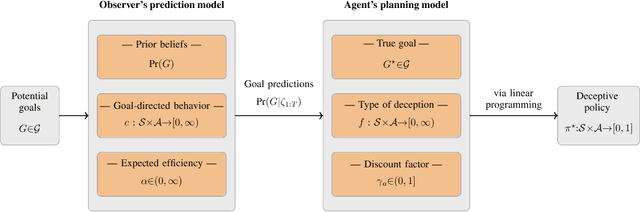
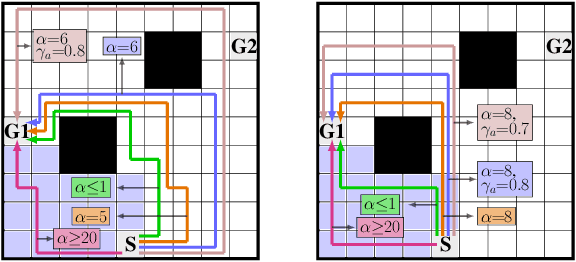
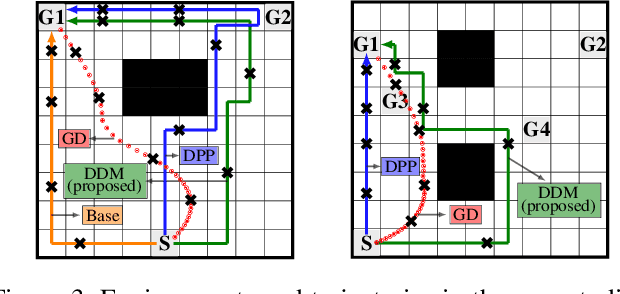
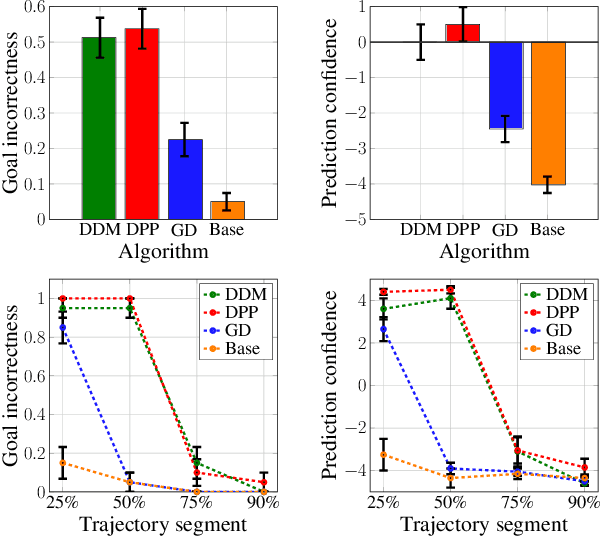
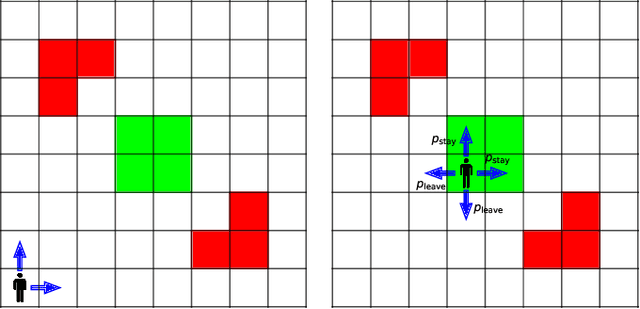
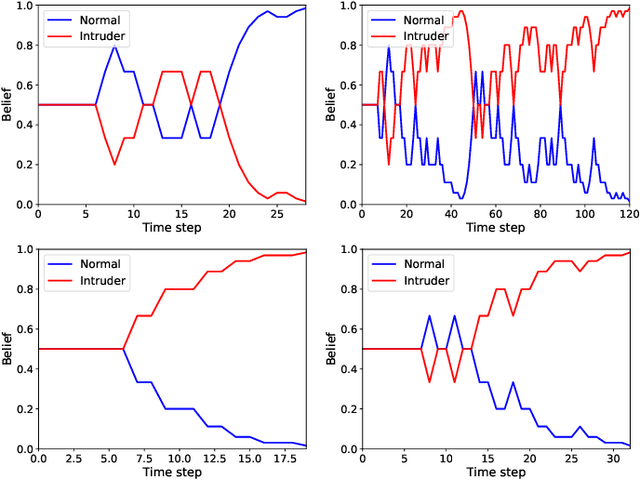
We study the design of autonomous agents that are capable of deceiving outside observers about their intentions while carrying out tasks in stochastic, complex environments. By modeling the agent's behavior as a Markov decision process, we consider a setting where the agent aims to reach one of multiple potential goals while deceiving outside observers about its true goal. We propose a novel approach to model observer predictions based on the principle of maximum entropy and to efficiently generate deceptive strategies via linear programming. The proposed approach enables the agent to exhibit a variety of tunable deceptive behaviors while ensuring the satisfaction of probabilistic constraints on the behavior. We evaluate the performance of the proposed approach via comparative user studies and present a case study on the streets of Manhattan, New York, using real travel time distributions.

Physical-Layer Security via Distributed Beamforming in the Presence of Adversaries with Unknown Locations

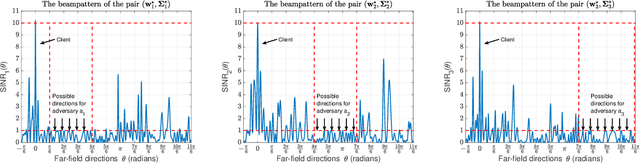
We study the problem of securely communicating a sequence of information bits with a client in the presence of multiple adversaries at unknown locations in the environment. We assume that the client and the adversaries are located in the far-field region, and all possible directions for each adversary can be expressed as a continuous interval of directions. In such a setting, we develop a periodic transmission strategy, i.e., a sequence of joint beamforming gain and artificial noise pairs, that prevents the adversaries from decreasing their uncertainty on the information sequence by eavesdropping on the transmission. We formulate a series of nonconvex semi-infinite optimization problems to synthesize the transmission strategy. We show that the semi-definite program (SDP) relaxations of these nonconvex problems are exact under an efficiently verifiable sufficient condition. We approximate the SDP relaxations, which are subject to infinitely many constraints, by randomly sampling a finite subset of the constraints and establish the probability with which optimal solutions to the obtained finite SDPs and the semi-infinite SDPs coincide. We demonstrate with numerical simulations that the proposed periodic strategy can ensure the security of communication in scenarios in which all stationary strategies fail to guarantee security.

Entropy Maximization for Markov Decision Processes Under Temporal Logic Constraints

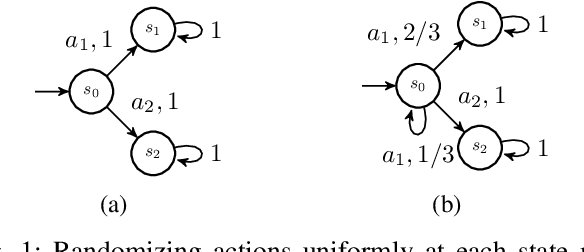
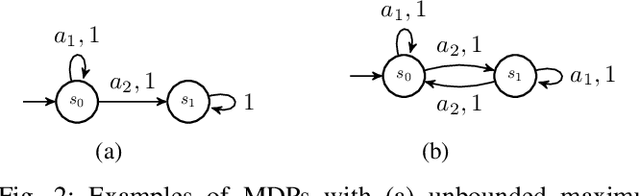
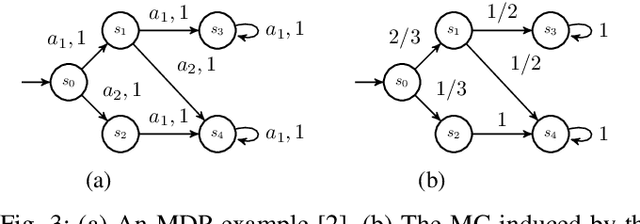
We study the problem of synthesizing a policy that maximizes the entropy of a Markov decision process (MDP) subject to a temporal logic constraint. Such a policy minimizes the predictability of the paths it generates, or dually, maximizes the continual exploration of different paths in an MDP while ensuring the satisfaction of a temporal logic specification. We first show that the maximum entropy of an MDP can be finite, infinite or unbounded. We provide necessary and sufficient conditions under which the maximum entropy of an MDP is finite, infinite or unbounded. We then present an algorithm to synthesize a policy that maximizes the entropy of an MDP. The proposed algorithm is based on a convex optimization problem and runs in time polynomial in the size of the MDP. We also show that maximizing the entropy of an MDP is equivalent to maximizing the entropy of the paths that reach a certain set of states in the MDP. Finally, we extend the algorithm to an MDP subject to a temporal logic specification. In numerical examples, we demonstrate the proposed method on different motion planning scenarios and illustrate that as the restrictions imposed on the paths by a specification increase, the maximum entropy decreases, which in turn, increases the predictability of paths.