Entropy Maximization for Markov Decision Processes Under Temporal Logic Constraints

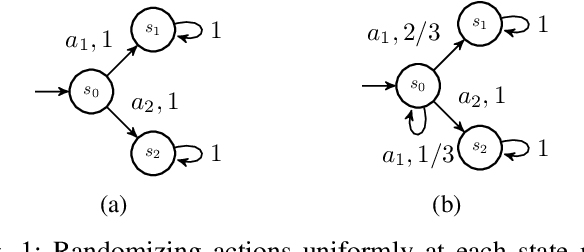
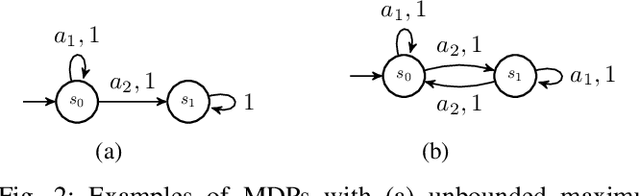
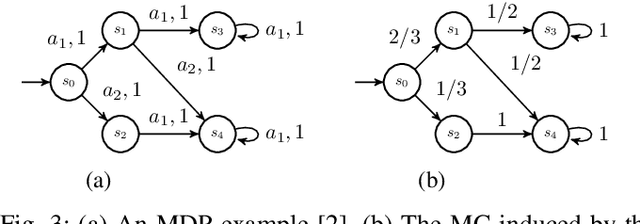
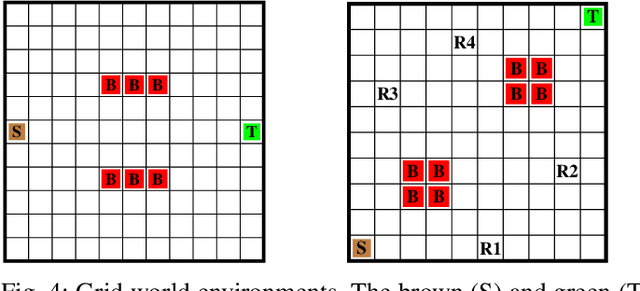
We study the problem of synthesizing a policy that maximizes the entropy of a Markov decision process (MDP) subject to a temporal logic constraint. Such a policy minimizes the predictability of the paths it generates, or dually, maximizes the continual exploration of different paths in an MDP while ensuring the satisfaction of a temporal logic specification. We first show that the maximum entropy of an MDP can be finite, infinite or unbounded. We provide necessary and sufficient conditions under which the maximum entropy of an MDP is finite, infinite or unbounded. We then present an algorithm to synthesize a policy that maximizes the entropy of an MDP. The proposed algorithm is based on a convex optimization problem and runs in time polynomial in the size of the MDP. We also show that maximizing the entropy of an MDP is equivalent to maximizing the entropy of the paths that reach a certain set of states in the MDP. Finally, we extend the algorithm to an MDP subject to a temporal logic specification. In numerical examples, we demonstrate the proposed method on different motion planning scenarios and illustrate that as the restrictions imposed on the paths by a specification increase, the maximum entropy decreases, which in turn, increases the predictability of paths.