Murat Cubuktepe
Formal Methods for Autonomous Systems
Nov 02, 2023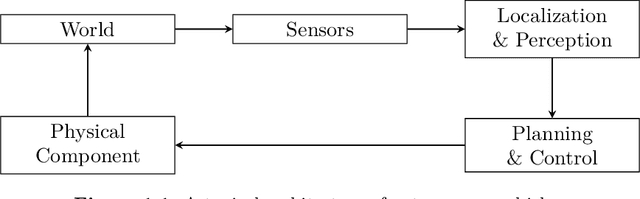
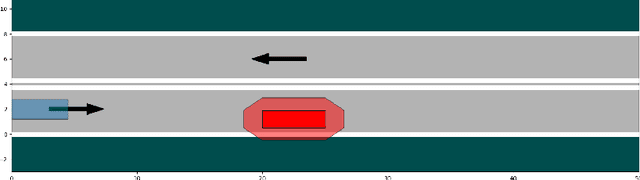
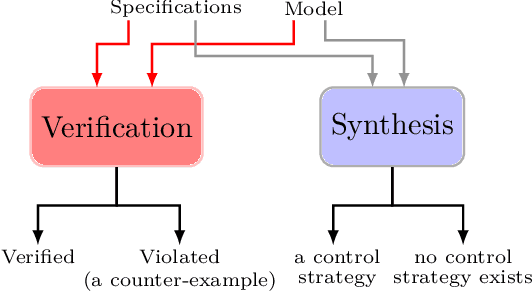
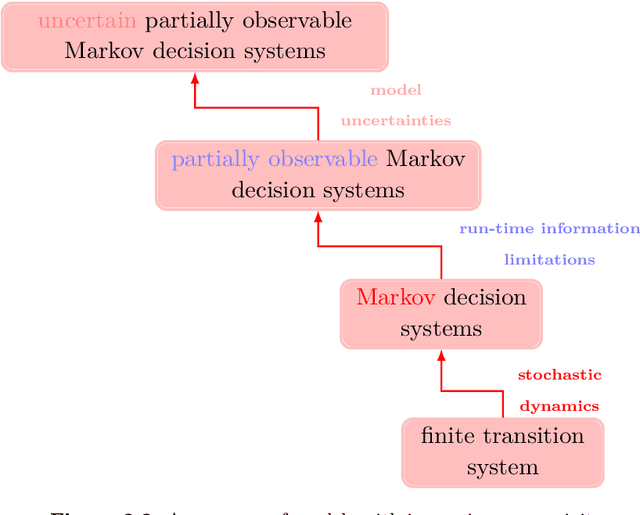
Abstract:Formal methods refer to rigorous, mathematical approaches to system development and have played a key role in establishing the correctness of safety-critical systems. The main building blocks of formal methods are models and specifications, which are analogous to behaviors and requirements in system design and give us the means to verify and synthesize system behaviors with formal guarantees. This monograph provides a survey of the current state of the art on applications of formal methods in the autonomous systems domain. We consider correct-by-construction synthesis under various formulations, including closed systems, reactive, and probabilistic settings. Beyond synthesizing systems in known environments, we address the concept of uncertainty and bound the behavior of systems that employ learning using formal methods. Further, we examine the synthesis of systems with monitoring, a mitigation technique for ensuring that once a system deviates from expected behavior, it knows a way of returning to normalcy. We also show how to overcome some limitations of formal methods themselves with learning. We conclude with future directions for formal methods in reinforcement learning, uncertainty, privacy, explainability of formal methods, and regulation and certification.
Verifiable Reinforcement Learning Systems via Compositionality
Sep 09, 2023Abstract:We propose a framework for verifiable and compositional reinforcement learning (RL) in which a collection of RL subsystems, each of which learns to accomplish a separate subtask, are composed to achieve an overall task. The framework consists of a high-level model, represented as a parametric Markov decision process, which is used to plan and analyze compositions of subsystems, and of the collection of low-level subsystems themselves. The subsystems are implemented as deep RL agents operating under partial observability. By defining interfaces between the subsystems, the framework enables automatic decompositions of task specifications, e.g., reach a target set of states with a probability of at least 0.95, into individual subtask specifications, i.e. achieve the subsystem's exit conditions with at least some minimum probability, given that its entry conditions are met. This in turn allows for the independent training and testing of the subsystems. We present theoretical results guaranteeing that if each subsystem learns a policy satisfying its subtask specification, then their composition is guaranteed to satisfy the overall task specification. Conversely, if the subtask specifications cannot all be satisfied by the learned policies, we present a method, formulated as the problem of finding an optimal set of parameters in the high-level model, to automatically update the subtask specifications to account for the observed shortcomings. The result is an iterative procedure for defining subtask specifications, and for training the subsystems to meet them. Experimental results demonstrate the presented framework's novel capabilities in environments with both full and partial observability, discrete and continuous state and action spaces, as well as deterministic and stochastic dynamics.
Task-Guided IRL in POMDPs that Scales
Dec 30, 2022



Abstract:In inverse reinforcement learning (IRL), a learning agent infers a reward function encoding the underlying task using demonstrations from experts. However, many existing IRL techniques make the often unrealistic assumption that the agent has access to full information about the environment. We remove this assumption by developing an algorithm for IRL in partially observable Markov decision processes (POMDPs). We address two limitations of existing IRL techniques. First, they require an excessive amount of data due to the information asymmetry between the expert and the learner. Second, most of these IRL techniques require solving the computationally intractable forward problem -- computing an optimal policy given a reward function -- in POMDPs. The developed algorithm reduces the information asymmetry while increasing the data efficiency by incorporating task specifications expressed in temporal logic into IRL. Such specifications may be interpreted as side information available to the learner a priori in addition to the demonstrations. Further, the algorithm avoids a common source of algorithmic complexity by building on causal entropy as the measure of the likelihood of the demonstrations as opposed to entropy. Nevertheless, the resulting problem is nonconvex due to the so-called forward problem. We solve the intrinsic nonconvexity of the forward problem in a scalable manner through a sequential linear programming scheme that guarantees to converge to a locally optimal policy. In a series of examples, including experiments in a high-fidelity Unity simulator, we demonstrate that even with a limited amount of data and POMDPs with tens of thousands of states, our algorithm learns reward functions and policies that satisfy the task while inducing similar behavior to the expert by leveraging the provided side information.
Convex Optimization for Parameter Synthesis in MDPs
Jun 30, 2021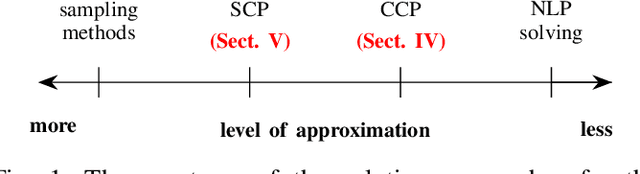
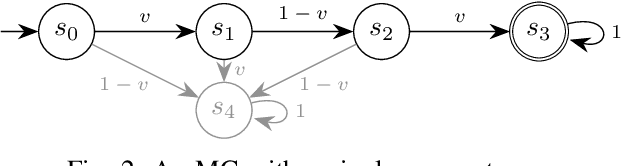
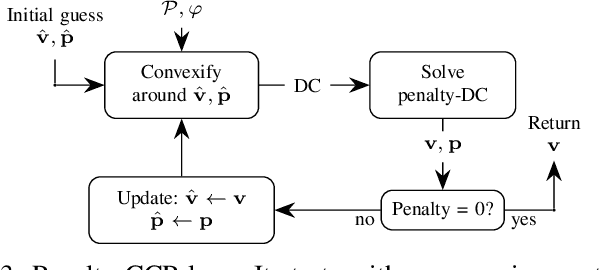
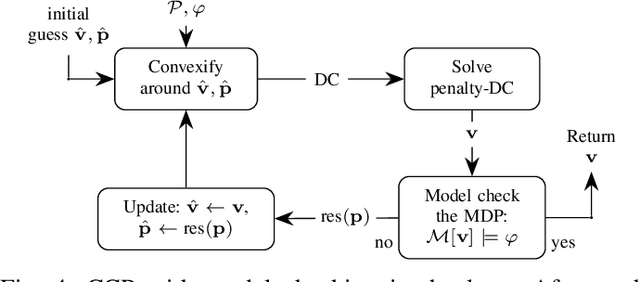
Abstract:Probabilistic model checking aims to prove whether a Markov decision process (MDP) satisfies a temporal logic specification. The underlying methods rely on an often unrealistic assumption that the MDP is precisely known. Consequently, parametric MDPs (pMDPs) extend MDPs with transition probabilities that are functions over unspecified parameters. The parameter synthesis problem is to compute an instantiation of these unspecified parameters such that the resulting MDP satisfies the temporal logic specification. We formulate the parameter synthesis problem as a quadratically constrained quadratic program (QCQP), which is nonconvex and is NP-hard to solve in general. We develop two approaches that iteratively obtain locally optimal solutions. The first approach exploits the so-called convex-concave procedure (CCP), and the second approach utilizes a sequential convex programming (SCP) method. The techniques improve the runtime and scalability by multiple orders of magnitude compared to black-box CCP and SCP by merging ideas from convex optimization and probabilistic model checking. We demonstrate the approaches on a satellite collision avoidance problem with hundreds of thousands of states and tens of thousands of parameters and their scalability on a wide range of commonly used benchmarks.
Verifiable and Compositional Reinforcement Learning Systems
Jun 07, 2021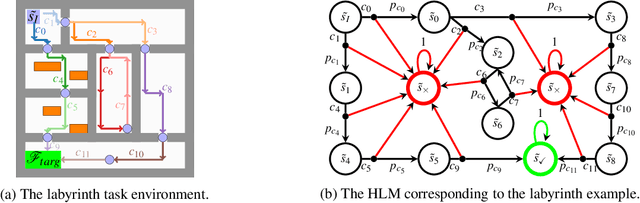

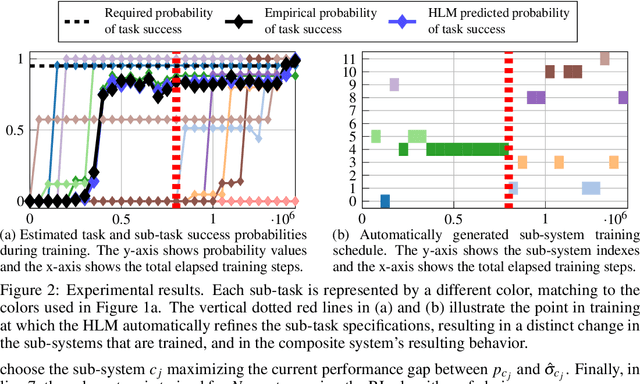

Abstract:We propose a novel framework for verifiable and compositional reinforcement learning (RL) in which a collection of RL sub-systems, each of which learns to accomplish a separate sub-task, are composed to achieve an overall task. The framework consists of a high-level model, represented as a parametric Markov decision process (pMDP) which is used to plan and to analyze compositions of sub-systems, and of the collection of low-level sub-systems themselves. By defining interfaces between the sub-systems, the framework enables automatic decompositons of task specifications, e.g., reach a target set of states with a probability of at least 0.95, into individual sub-task specifications, i.e. achieve the sub-system's exit conditions with at least some minimum probability, given that its entry conditions are met. This in turn allows for the independent training and testing of the sub-systems; if they each learn a policy satisfying the appropriate sub-task specification, then their composition is guaranteed to satisfy the overall task specification. Conversely, if the sub-task specifications cannot all be satisfied by the learned policies, we present a method, formulated as the problem of finding an optimal set of parameters in the pMDP, to automatically update the sub-task specifications to account for the observed shortcomings. The result is an iterative procedure for defining sub-task specifications, and for training the sub-systems to meet them. As an additional benefit, this procedure allows for particularly challenging or important components of an overall task to be determined automatically, and focused on, during training. Experimental results demonstrate the presented framework's novel capabilities.
Task-Guided Inverse Reinforcement Learning Under Partial Information
May 28, 2021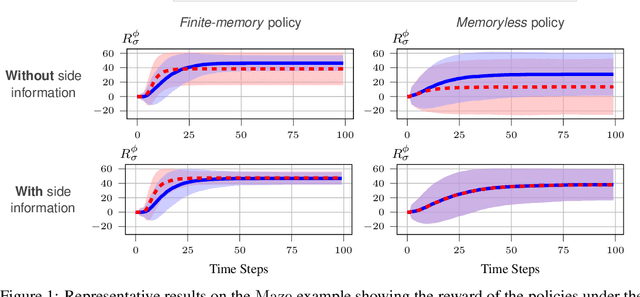
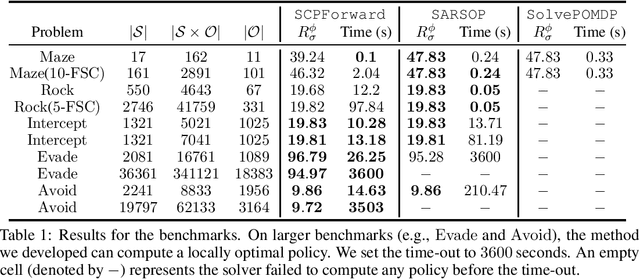
Abstract:We study the problem of inverse reinforcement learning (IRL), where the learning agent recovers a reward function using expert demonstrations. Most of the existing IRL techniques make the often unrealistic assumption that the agent has access to full information about the environment. We remove this assumption by developing an algorithm for IRL in partially observable Markov decision processes (POMDPs), where an agent cannot directly observe the current state of the POMDP. The algorithm addresses several limitations of existing techniques that do not take the \emph{information asymmetry} between the expert and the agent into account. First, it adopts causal entropy as the measure of the likelihood of the expert demonstrations as opposed to entropy in most existing IRL techniques and avoids a common source of algorithmic complexity. Second, it incorporates task specifications expressed in temporal logic into IRL. Such specifications may be interpreted as side information available to the learner a priori in addition to the demonstrations, and may reduce the information asymmetry between the expert and the agent. Nevertheless, the resulting formulation is still nonconvex due to the intrinsic nonconvexity of the so-called \emph{forward problem}, i.e., computing an optimal policy given a reward function, in POMDPs. We address this nonconvexity through sequential convex programming and introduce several extensions to solve the forward problem in a scalable manner. This scalability allows computing policies that incorporate memory at the expense of added computational cost yet also achieves higher performance compared to memoryless policies. We demonstrate that, even with severely limited data, the algorithm learns reward functions and policies that satisfy the task and induce a similar behavior to the expert by leveraging the side information and incorporating memory into the policy.
Polynomial-Time Algorithms for Multi-Agent Minimal-Capacity Planning
May 04, 2021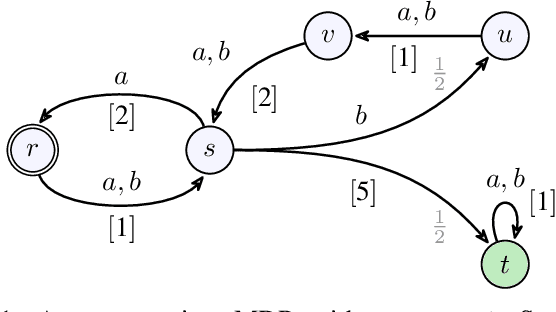
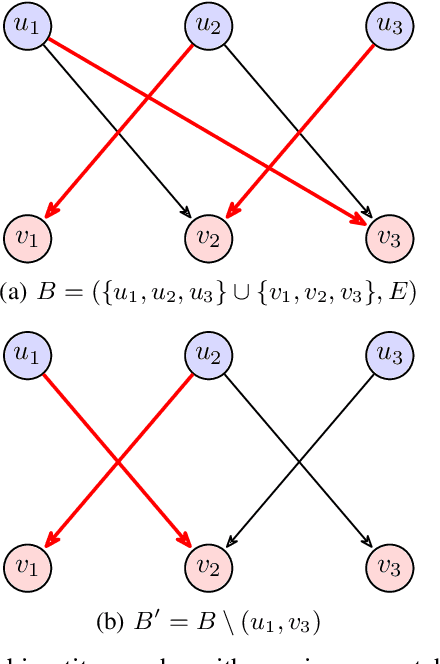
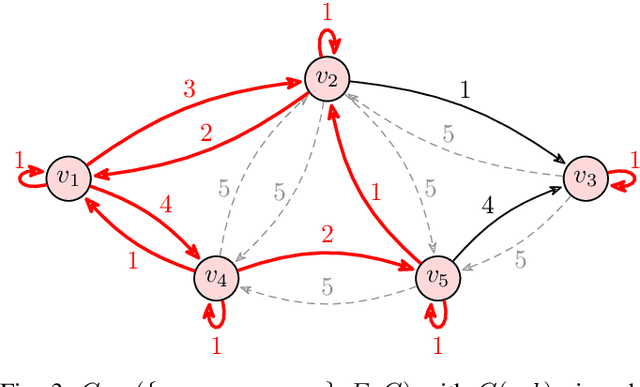
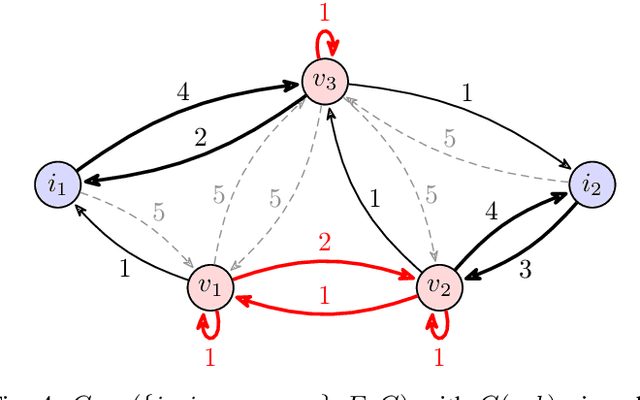
Abstract:We study the problem of minimizing the resource capacity of autonomous agents cooperating to achieve a shared task. More specifically, we consider high-level planning for a team of homogeneous agents that operate under resource constraints in stochastic environments and share a common goal: given a set of target locations, ensure that each location will be visited infinitely often by some agent almost surely. We formalize the dynamics of agents by consumption Markov decision processes. In a consumption Markov decision process, the agent has a resource of limited capacity. Each action of the agent may consume some amount of the resource. To avoid exhaustion, the agent can replenish its resource to full capacity in designated reload states. The resource capacity restricts the capabilities of the agent. The objective is to assign target locations to agents, and each agent is only responsible for visiting the assigned subset of target locations repeatedly. Moreover, the assignment must ensure that the agents can carry out their tasks with minimal resource capacity. We reduce the problem of finding target assignments for a team of agents with the lowest possible capacity to an equivalent graph-theoretical problem. We develop an algorithm that solves this graph problem in time that is \emph{polynomial} in the number of agents, target locations, and size of the consumption Markov decision process. We demonstrate the applicability and scalability of the algorithm in a scenario where hundreds of unmanned underwater vehicles monitor hundreds of locations in environments with stochastic ocean currents.
Robust Finite-State Controllers for Uncertain POMDPs
Sep 24, 2020
Abstract:Uncertain partially observable Markov decision processes (uPOMDPs) allow the probabilistic transition and observation functions of standard POMDPs to belong to a so-called uncertainty set. Such uncertainty sets capture uncountable sets of probability distributions. We develop an algorithm to compute finite-memory policies for uPOMDPs that robustly satisfy given specifications against any admissible distribution. In general, computing such policies is both theoretically and practically intractable. We provide an efficient solution to this problem in four steps. (1) We state the underlying problem as a nonconvex optimization problem with infinitely many constraints. (2) A dedicated dualization scheme yields a dual problem that is still nonconvex but has finitely many constraints. (3) We linearize this dual problem and (4) solve the resulting finite linear program to obtain locally optimal solutions to the original problem. The resulting problem formulation is exponentially smaller than those resulting from existing methods. We demonstrate the applicability of our algorithm using large instances of an aircraft collision-avoidance scenario and a novel spacecraft motion planning case study.
Scalable Synthesis of Minimum-Information Linear-Gaussian Control by Distributed Optimization
Apr 11, 2020
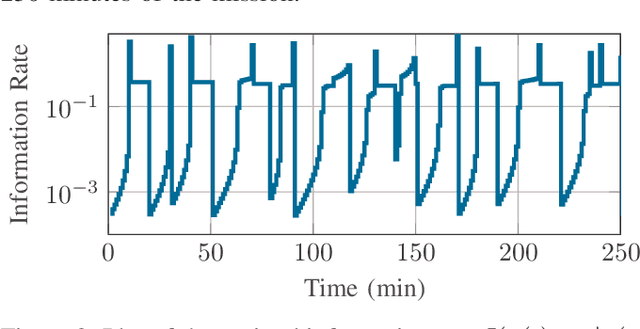
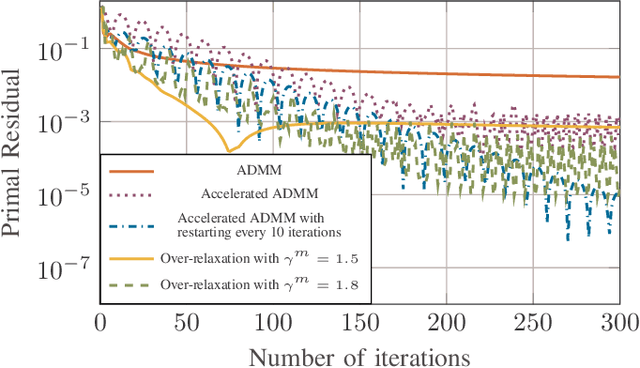
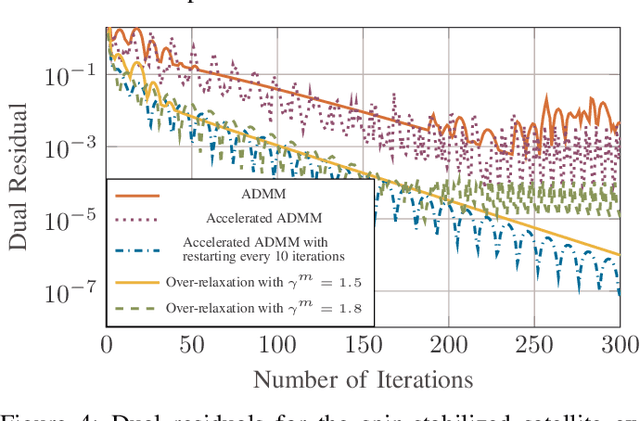
Abstract:We consider a discrete-time linear-quadratic Gaussian control problem in which we minimize a weighted sum of the directed information from the state of the system to the control input and the control cost. The optimal control and sensing policies can be synthesized jointly by solving a semidefinite programming problem. However, the existing solutions typically scale cubic with the horizon length. We leverage the structure in the problem to develop a distributed algorithm that decomposes the synthesis problem into a set of smaller problems, one for each time step. We prove that the algorithm runs in time linear in the horizon length. As an application of the algorithm, we consider a path-planning problem in a state space with obstacles under the presence of stochastic disturbances. The algorithm computes a locally optimal solution that jointly minimizes the perception and control cost while ensuring the safety of the path. The numerical examples show that the algorithm can scale to thousands of horizon length and compute locally optimal solutions.
Synthesis of Provably Correct Autonomy Protocols for Shared Control
May 15, 2019
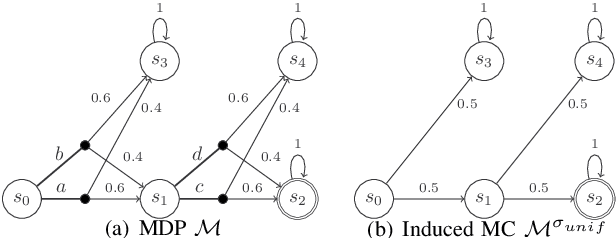
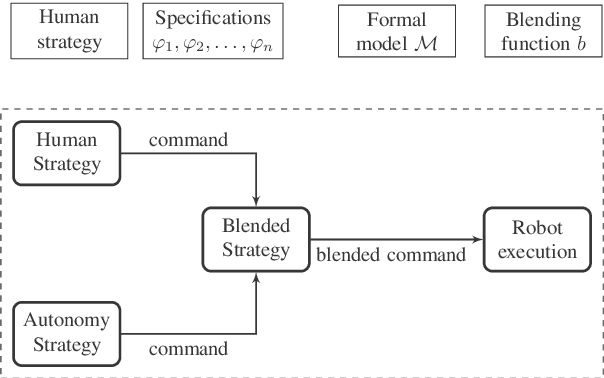

Abstract:We synthesize shared control protocols subject to probabilistic temporal logic specifications. More specifically, we develop a framework in which a human and an autonomy protocol can issue commands to carry out a certain task. We blend these commands into a joint input to a robot. We model the interaction between the human and the robot as a Markov decision process (MDP) that represents the shared control scenario. Using inverse reinforcement learning, we obtain an abstraction of the human's behavior and decisions. We use randomized strategies to account for randomness in human's decisions, caused by factors such as complexity of the task specifications or imperfect interfaces. We design the autonomy protocol to ensure that the resulting robot behavior satisfies given safety and performance specifications in probabilistic temporal logic. Additionally, the resulting strategies generate behavior as similar to the behavior induced by the human's commands as possible. We solve the underlying problem efficiently using quasiconvex programming. Case studies involving autonomous wheelchair navigation and unmanned aerial vehicle mission planning showcase the applicability of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge