Neural Port-Hamiltonian Differential Algebraic Equations for Compositional Learning of Electrical Networks

We develop compositional learning algorithms for coupled dynamical systems. While deep learning has proven effective at modeling complex relationships from data, compositional couplings between system components typically introduce algebraic constraints on state variables, posing challenges to many existing data-driven approaches to modeling dynamical systems. Towards developing deep learning models for constrained dynamical systems, we introduce neural port-Hamiltonian differential algebraic equations (N-PHDAEs), which use neural networks to parametrize unknown terms in both the differential and algebraic components of a port-Hamiltonian DAE. To train these models, we propose an algorithm that uses automatic differentiation to perform index reduction, automatically transforming the neural DAE into an equivalent system of neural ordinary differential equations (N-ODEs), for which established model inference and backpropagation methods exist. The proposed compositional modeling framework and learning algorithms may be applied broadly to learn control-oriented models of dynamical systems in a variety of application areas, however, in this work, we focus on their application to the modeling of electrical networks. Experiments simulating the dynamics of nonlinear circuits exemplify the benefits of our approach: the proposed N-PHDAE model achieves an order of magnitude improvement in prediction accuracy and constraint satisfaction when compared to a baseline N-ODE over long prediction time horizons. We also validate the compositional capabilities of our approach through experiments on a simulated D.C. microgrid: we train individual N-PHDAE models for separate grid components, before coupling them to accurately predict the behavior of larger-scale networks.

A Multifidelity Sim-to-Real Pipeline for Verifiable and Compositional Reinforcement Learning

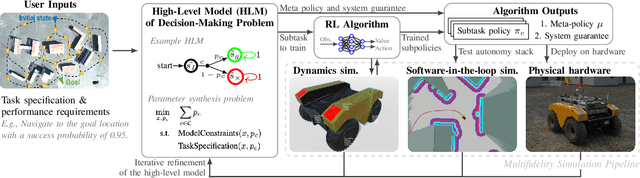
We propose and demonstrate a compositional framework for training and verifying reinforcement learning (RL) systems within a multifidelity sim-to-real pipeline, in order to deploy reliable and adaptable RL policies on physical hardware. By decomposing complex robotic tasks into component subtasks and defining mathematical interfaces between them, the framework allows for the independent training and testing of the corresponding subtask policies, while simultaneously providing guarantees on the overall behavior that results from their composition. By verifying the performance of these subtask policies using a multifidelity simulation pipeline, the framework not only allows for efficient RL training, but also for a refinement of the subtasks and their interfaces in response to challenges arising from discrepancies between simulation and reality. In an experimental case study we apply the framework to train and deploy a compositional RL system that successfully pilots a Warthog unmanned ground robot.

Formal Methods for Autonomous Systems

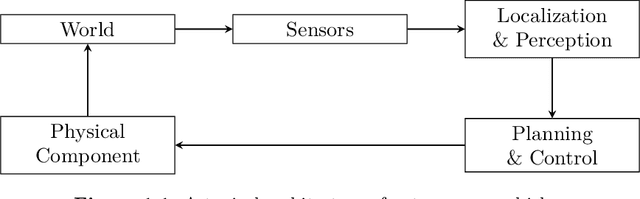
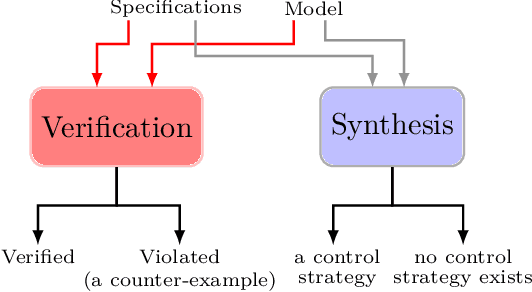
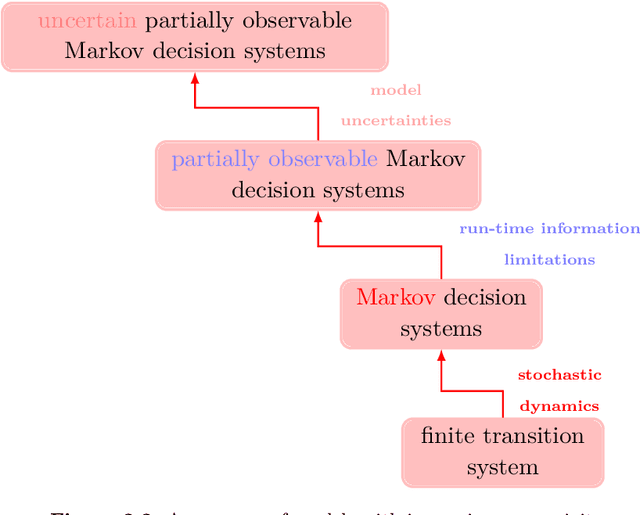
Formal methods refer to rigorous, mathematical approaches to system development and have played a key role in establishing the correctness of safety-critical systems. The main building blocks of formal methods are models and specifications, which are analogous to behaviors and requirements in system design and give us the means to verify and synthesize system behaviors with formal guarantees. This monograph provides a survey of the current state of the art on applications of formal methods in the autonomous systems domain. We consider correct-by-construction synthesis under various formulations, including closed systems, reactive, and probabilistic settings. Beyond synthesizing systems in known environments, we address the concept of uncertainty and bound the behavior of systems that employ learning using formal methods. Further, we examine the synthesis of systems with monitoring, a mitigation technique for ensuring that once a system deviates from expected behavior, it knows a way of returning to normalcy. We also show how to overcome some limitations of formal methods themselves with learning. We conclude with future directions for formal methods in reinforcement learning, uncertainty, privacy, explainability of formal methods, and regulation and certification.

Verifiable Reinforcement Learning Systems via Compositionality

We propose a framework for verifiable and compositional reinforcement learning (RL) in which a collection of RL subsystems, each of which learns to accomplish a separate subtask, are composed to achieve an overall task. The framework consists of a high-level model, represented as a parametric Markov decision process, which is used to plan and analyze compositions of subsystems, and of the collection of low-level subsystems themselves. The subsystems are implemented as deep RL agents operating under partial observability. By defining interfaces between the subsystems, the framework enables automatic decompositions of task specifications, e.g., reach a target set of states with a probability of at least 0.95, into individual subtask specifications, i.e. achieve the subsystem's exit conditions with at least some minimum probability, given that its entry conditions are met. This in turn allows for the independent training and testing of the subsystems. We present theoretical results guaranteeing that if each subsystem learns a policy satisfying its subtask specification, then their composition is guaranteed to satisfy the overall task specification. Conversely, if the subtask specifications cannot all be satisfied by the learned policies, we present a method, formulated as the problem of finding an optimal set of parameters in the high-level model, to automatically update the subtask specifications to account for the observed shortcomings. The result is an iterative procedure for defining subtask specifications, and for training the subsystems to meet them. Experimental results demonstrate the presented framework's novel capabilities in environments with both full and partial observability, discrete and continuous state and action spaces, as well as deterministic and stochastic dynamics.

Multimodal Pretrained Models for Sequential Decision-Making: Synthesis, Verification, Grounding, and Perception

Recently developed pretrained models can encode rich world knowledge expressed in multiple modalities, such as text and images. However, the outputs of these models cannot be integrated into algorithms to solve sequential decision-making tasks. We develop an algorithm that utilizes the knowledge from pretrained models to construct and verify controllers for sequential decision-making tasks, and to ground these controllers to task environments through visual observations. In particular, the algorithm queries a pretrained model with a user-provided, text-based task description and uses the model's output to construct an automaton-based controller that encodes the model's task-relevant knowledge. It then verifies whether the knowledge encoded in the controller is consistent with other independently available knowledge, which may include abstract information on the environment or user-provided specifications. If this verification step discovers any inconsistency, the algorithm automatically refines the controller to resolve the inconsistency. Next, the algorithm leverages the vision and language capabilities of pretrained models to ground the controller to the task environment. It collects image-based observations from the task environment and uses the pretrained model to link these observations to the text-based control logic encoded in the controller (e.g., actions and conditions that trigger the actions). We propose a mechanism to ensure the controller satisfies the user-provided specification even when perceptual uncertainties are present. We demonstrate the algorithm's ability to construct, verify, and ground automaton-based controllers through a suite of real-world tasks, including daily life and robot manipulation tasks.

How to Learn and Generalize From Three Minutes of Data: Physics-Constrained and Uncertainty-Aware Neural Stochastic Differential Equations

We present a framework and algorithms to learn controlled dynamics models using neural stochastic differential equations (SDEs) -- SDEs whose drift and diffusion terms are both parametrized by neural networks. We construct the drift term to leverage a priori physics knowledge as inductive bias, and we design the diffusion term to represent a distance-aware estimate of the uncertainty in the learned model's predictions -- it matches the system's underlying stochasticity when evaluated on states near those from the training dataset, and it predicts highly stochastic dynamics when evaluated on states beyond the training regime. The proposed neural SDEs can be evaluated quickly enough for use in model predictive control algorithms, or they can be used as simulators for model-based reinforcement learning. Furthermore, they make accurate predictions over long time horizons, even when trained on small datasets that cover limited regions of the state space. We demonstrate these capabilities through experiments on simulated robotic systems, as well as by using them to model and control a hexacopter's flight dynamics: A neural SDE trained using only three minutes of manually collected flight data results in a model-based control policy that accurately tracks aggressive trajectories that push the hexacopter's velocity and Euler angles to nearly double the maximum values observed in the training dataset.

Differential Privacy in Cooperative Multiagent Planning

Privacy-aware multiagent systems must protect agents' sensitive data while simultaneously ensuring that agents accomplish their shared objectives. Towards this goal, we propose a framework to privatize inter-agent communications in cooperative multiagent decision-making problems. We study sequential decision-making problems formulated as cooperative Markov games with reach-avoid objectives. We apply a differential privacy mechanism to privatize agents' communicated symbolic state trajectories, and then we analyze tradeoffs between the strength of privacy and the team's performance. For a given level of privacy, this tradeoff is shown to depend critically upon the total correlation among agents' state-action processes. We synthesize policies that are robust to privacy by reducing the value of the total correlation. Numerical experiments demonstrate that the team's performance under these policies decreases by only 3 percent when comparing private versus non-private implementations of communication. By contrast, the team's performance decreases by roughly 86 percent when using baseline policies that ignore total correlation and only optimize team performance.

Physics-Informed Kernel Embeddings: Integrating Prior System Knowledge with Data-Driven Control

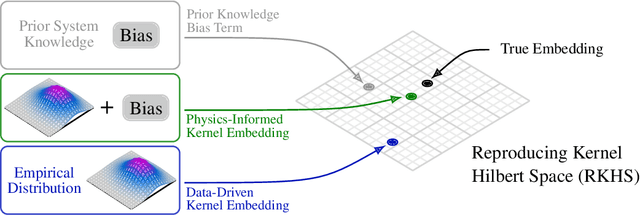
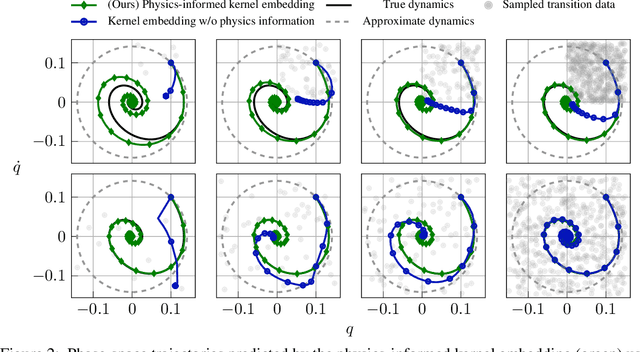
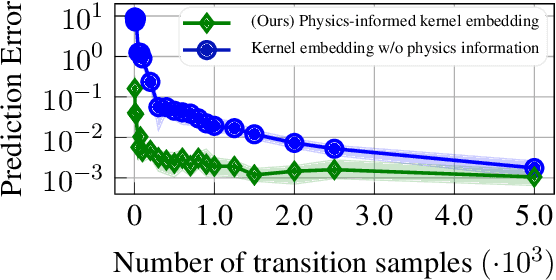
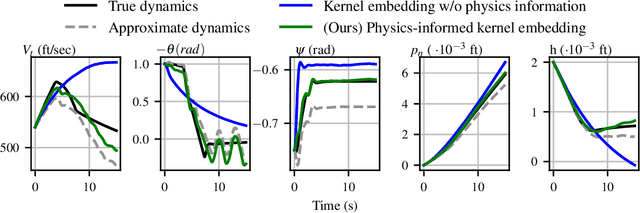
Data-driven control algorithms use observations of system dynamics to construct an implicit model for the purpose of control. However, in practice, data-driven techniques often require excessive sample sizes, which may be infeasible in real-world scenarios where only limited observations of the system are available. Furthermore, purely data-driven methods often neglect useful a priori knowledge, such as approximate models of the system dynamics. We present a method to incorporate such prior knowledge into data-driven control algorithms using kernel embeddings, a nonparametric machine learning technique based in the theory of reproducing kernel Hilbert spaces. Our proposed approach incorporates prior knowledge of the system dynamics as a bias term in the kernel learning problem. We formulate the biased learning problem as a least-squares problem with a regularization term that is informed by the dynamics, that has an efficiently computable, closed-form solution. Through numerical experiments, we empirically demonstrate the improved sample efficiency and out-of-sample generalization of our approach over a purely data-driven baseline. We demonstrate an application of our method to control through a target tracking problem with nonholonomic dynamics, and on spring-mass-damper and F-16 aircraft state prediction tasks.

Compositional Learning of Dynamical System Models Using Port-Hamiltonian Neural Networks

Many dynamical systems -- from robots interacting with their surroundings to large-scale multiphysics systems -- involve a number of interacting subsystems. Toward the objective of learning composite models of such systems from data, we present i) a framework for compositional neural networks, ii) algorithms to train these models, iii) a method to compose the learned models, iv) theoretical results that bound the error of the resulting composite models, and v) a method to learn the composition itself, when it is not known a prior. The end result is a modular approach to learning: neural network submodels are trained on trajectory data generated by relatively simple subsystems, and the dynamics of more complex composite systems are then predicted without requiring additional data generated by the composite systems themselves. We achieve this compositionality by representing the system of interest, as well as each of its subsystems, as a port-Hamiltonian neural network (PHNN) -- a class of neural ordinary differential equations that uses the port-Hamiltonian systems formulation as inductive bias. We compose collections of PHNNs by using the system's physics-informed interconnection structure, which may be known a priori, or may itself be learned from data. We demonstrate the novel capabilities of the proposed framework through numerical examples involving interacting spring-mass-damper systems. Models of these systems, which include nonlinear energy dissipation and control inputs, are learned independently. Accurate compositions are learned using an amount of training data that is negligible in comparison with that required to train a new model from scratch. Finally, we observe that the composite PHNNs enjoy properties of port-Hamiltonian systems, such as cyclo-passivity -- a property that is useful for control purposes.

Planning Not to Talk: Multiagent Systems that are Robust to Communication Loss

In a cooperative multiagent system, a collection of agents executes a joint policy in order to achieve some common objective. The successful deployment of such systems hinges on the availability of reliable inter-agent communication. However, many sources of potential disruption to communication exist in practice, such as radio interference, hardware failure, and adversarial attacks. In this work, we develop joint policies for cooperative multiagent systems that are robust to potential losses in communication. More specifically, we develop joint policies for cooperative Markov games with reach-avoid objectives. First, we propose an algorithm for the decentralized execution of joint policies during periods of communication loss. Next, we use the total correlation of the state-action process induced by a joint policy as a measure of the intrinsic dependencies between the agents. We then use this measure to lower-bound the performance of a joint policy when communication is lost. Finally, we present an algorithm that maximizes a proxy to this lower bound in order to synthesize minimum-dependency joint policies that are robust to communication loss. Numerical experiments show that the proposed minimum-dependency policies require minimal coordination between the agents while incurring little to no loss in performance; the total correlation value of the synthesized policy is one fifth of the total correlation value of the baseline policy which does not take potential communication losses into account. As a result, the performance of the minimum-dependency policies remains consistently high regardless of whether or not communication is available. By contrast, the performance of the baseline policy decreases by twenty percent when communication is lost.