Physics-Informed Kernel Embeddings: Integrating Prior System Knowledge with Data-Driven Control

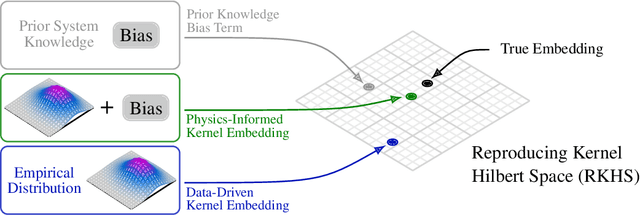
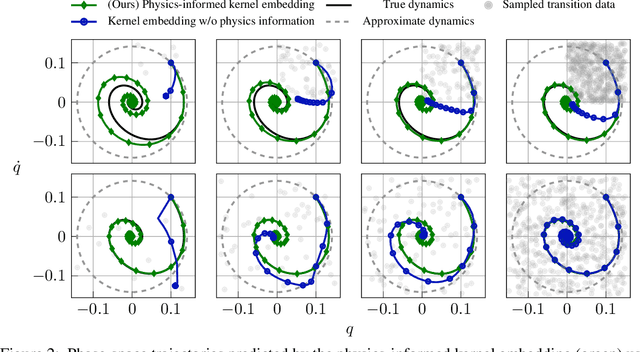
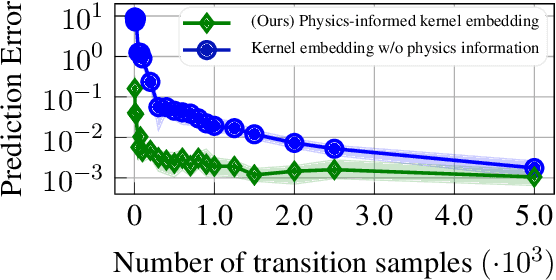
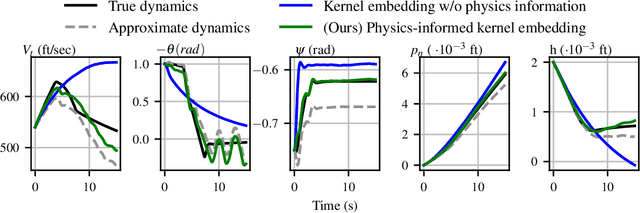
Data-driven control algorithms use observations of system dynamics to construct an implicit model for the purpose of control. However, in practice, data-driven techniques often require excessive sample sizes, which may be infeasible in real-world scenarios where only limited observations of the system are available. Furthermore, purely data-driven methods often neglect useful a priori knowledge, such as approximate models of the system dynamics. We present a method to incorporate such prior knowledge into data-driven control algorithms using kernel embeddings, a nonparametric machine learning technique based in the theory of reproducing kernel Hilbert spaces. Our proposed approach incorporates prior knowledge of the system dynamics as a bias term in the kernel learning problem. We formulate the biased learning problem as a least-squares problem with a regularization term that is informed by the dynamics, that has an efficiently computable, closed-form solution. Through numerical experiments, we empirically demonstrate the improved sample efficiency and out-of-sample generalization of our approach over a purely data-driven baseline. We demonstrate an application of our method to control through a target tracking problem with nonholonomic dynamics, and on spring-mass-damper and F-16 aircraft state prediction tasks.

Probabilistic Verification of ReLU Neural Networks via Characteristic Functions

Verifying the input-output relationships of a neural network so as to achieve some desired performance specification is a difficult, yet important, problem due to the growing ubiquity of neural nets in many engineering applications. We use ideas from probability theory in the frequency domain to provide probabilistic verification guarantees for ReLU neural networks. Specifically, we interpret a (deep) feedforward neural network as a discrete dynamical system over a finite horizon that shapes distributions of initial states, and use characteristic functions to propagate the distribution of the input data through the network. Using the inverse Fourier transform, we obtain the corresponding cumulative distribution function of the output set, which can be used to check if the network is performing as expected given any random point from the input set. The proposed approach does not require distributions to have well-defined moments or moment generating functions. We demonstrate our proposed approach on two examples, and compare its performance to related approaches.

SOCKS: A Stochastic Optimal Control and Reachability Toolbox Using Kernel Methods

We present SOCKS, a data-driven stochastic optimal control toolbox based in kernel methods. SOCKS is a collection of data-driven algorithms that compute approximate solutions to stochastic optimal control problems with arbitrary cost and constraint functions, including stochastic reachability, which seeks to determine the likelihood that a system will reach a desired target set while respecting a set of pre-defined safety constraints. Our approach relies upon a class of machine learning algorithms based in kernel methods, a nonparametric technique which can be used to represent probability distributions in a high-dimensional space of functions known as a reproducing kernel Hilbert space. As a nonparametric technique, kernel methods are inherently data-driven, meaning that they do not place prior assumptions on the system dynamics or the structure of the uncertainty. This makes the toolbox amenable to a wide variety of systems, including those with nonlinear dynamics, black-box elements, and poorly characterized stochastic disturbances. We present the main features of SOCKS and demonstrate its capabilities on several benchmarks.

Data-Driven Chance Constrained Control using Kernel Distribution Embeddings

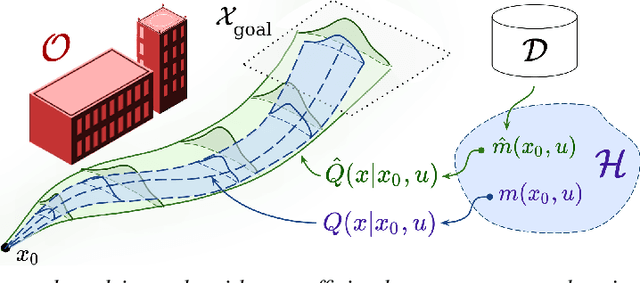
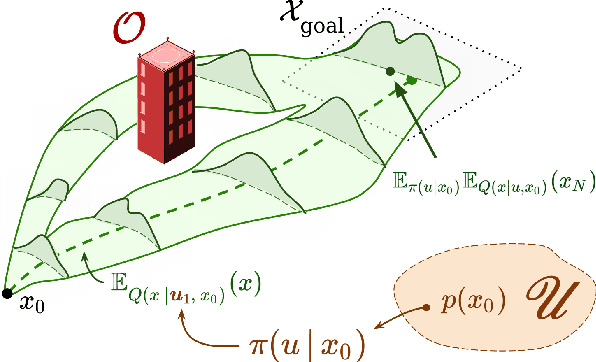
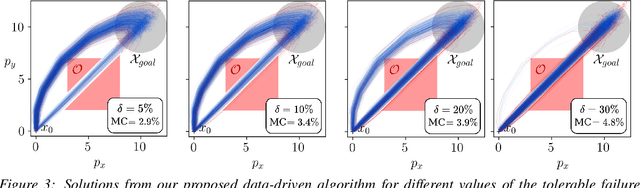
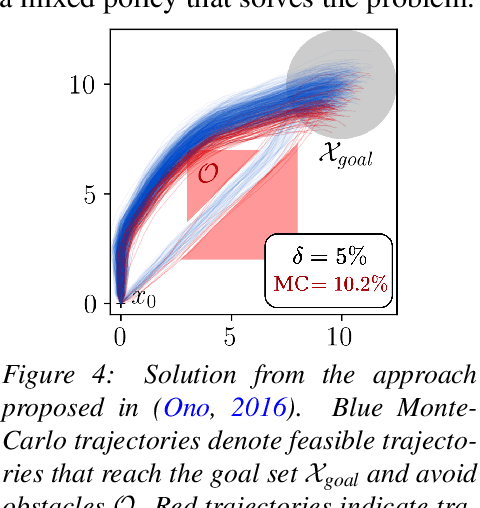
We present a data-driven algorithm for efficiently computing stochastic control policies for general joint chance constrained optimal control problems. Our approach leverages the theory of kernel distribution embeddings, which allows representing expectation operators as inner products in a reproducing kernel Hilbert space. This framework enables approximately reformulating the original problem using a dataset of observed trajectories from the system without imposing prior assumptions on the parameterization of the system dynamics or the structure of the uncertainty. By optimizing over a finite subset of stochastic open-loop control trajectories, we relax the original problem to a linear program over the control parameters that can be efficiently solved using standard convex optimization techniques. We demonstrate our proposed approach in simulation on a system with nonlinear non-Markovian dynamics navigating in a cluttered environment.