Data-Driven Chance Constrained Control using Kernel Distribution Embeddings
Paper and Code
Feb 08, 2022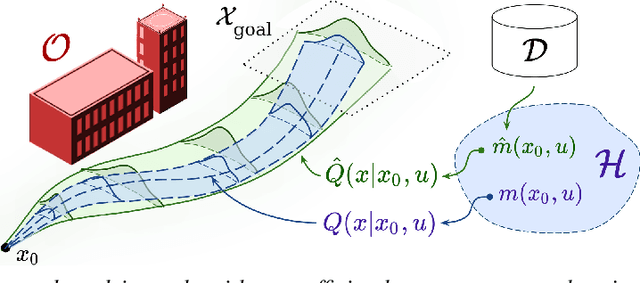
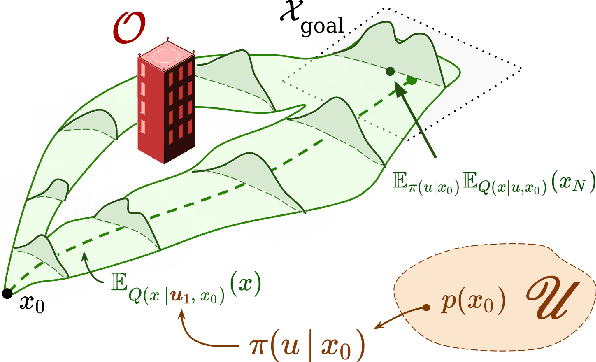
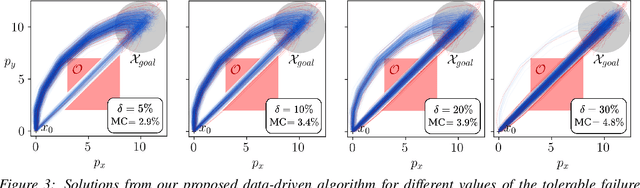
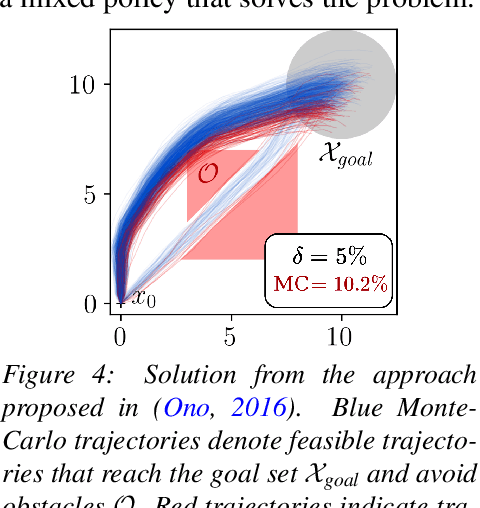
We present a data-driven algorithm for efficiently computing stochastic control policies for general joint chance constrained optimal control problems. Our approach leverages the theory of kernel distribution embeddings, which allows representing expectation operators as inner products in a reproducing kernel Hilbert space. This framework enables approximately reformulating the original problem using a dataset of observed trajectories from the system without imposing prior assumptions on the parameterization of the system dynamics or the structure of the uncertainty. By optimizing over a finite subset of stochastic open-loop control trajectories, we relax the original problem to a linear program over the control parameters that can be efficiently solved using standard convex optimization techniques. We demonstrate our proposed approach in simulation on a system with nonlinear non-Markovian dynamics navigating in a cluttered environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge