Zero-Shot Transfer of Neural ODEs

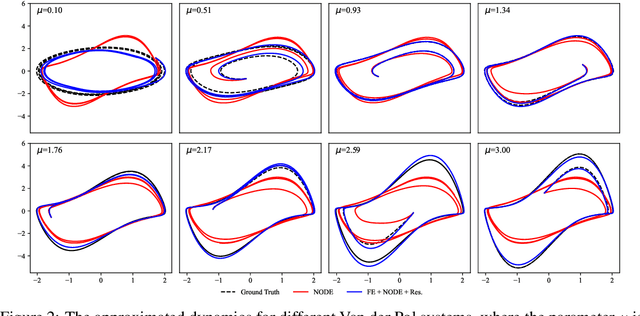
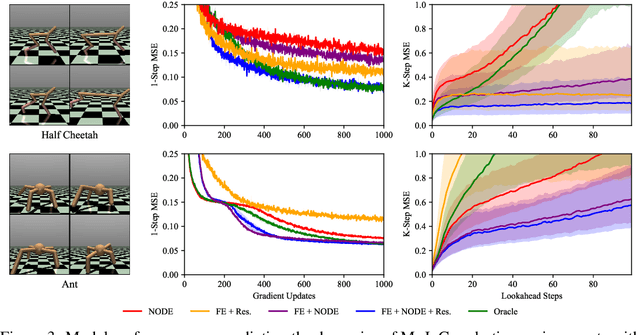
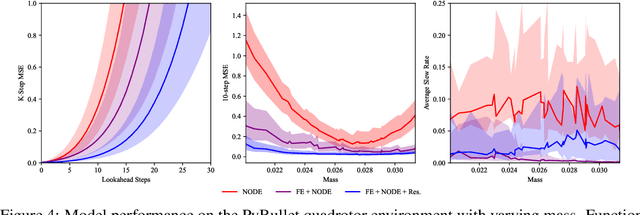
Autonomous systems often encounter environments and scenarios beyond the scope of their training data, which underscores a critical challenge: the need to generalize and adapt to unseen scenarios in real time. This challenge necessitates new mathematical and algorithmic tools that enable adaptation and zero-shot transfer. To this end, we leverage the theory of function encoders, which enables zero-shot transfer by combining the flexibility of neural networks with the mathematical principles of Hilbert spaces. Using this theory, we first present a method for learning a space of dynamics spanned by a set of neural ODE basis functions. After training, the proposed approach can rapidly identify dynamics in the learned space using an efficient inner product calculation. Critically, this calculation requires no gradient calculations or retraining during the online phase. This method enables zero-shot transfer for autonomous systems at runtime and opens the door for a new class of adaptable control algorithms. We demonstrate state-of-the-art system modeling accuracy for two MuJoCo robot environments and show that the learned models can be used for more efficient MPC control of a quadrotor.

Active Learning of Dynamics Using Prior Domain Knowledge in the Sampling Process

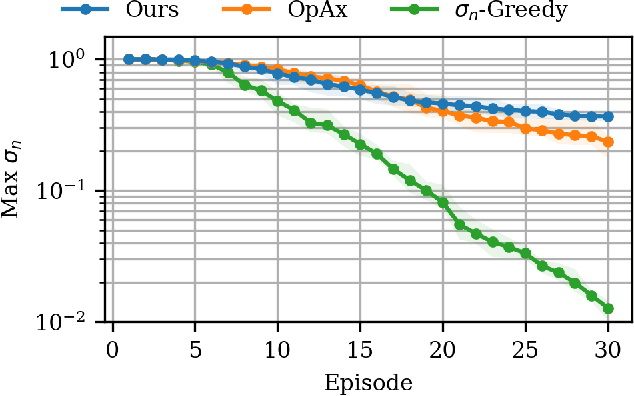
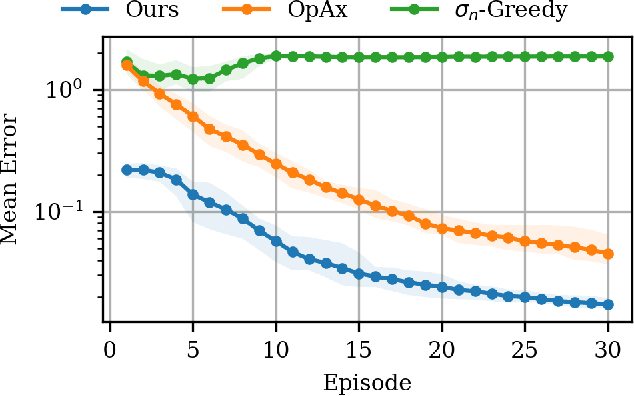
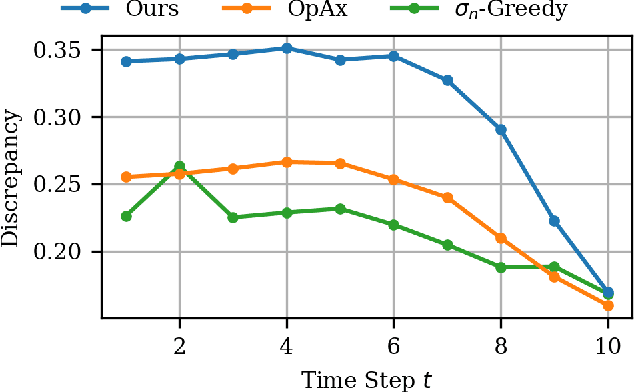
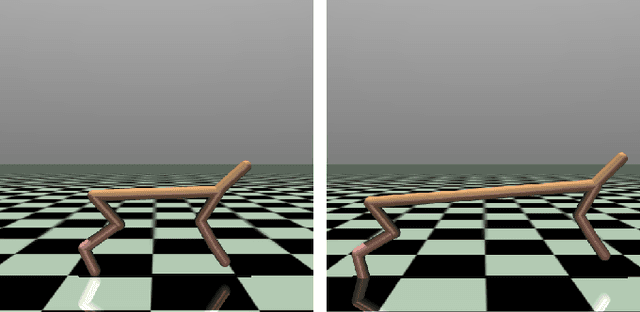
We present an active learning algorithm for learning dynamics that leverages side information by explicitly incorporating prior domain knowledge into the sampling process. Our proposed algorithm guides the exploration toward regions that demonstrate high empirical discrepancy between the observed data and an imperfect prior model of the dynamics derived from side information. Through numerical experiments, we demonstrate that this strategy explores regions of high discrepancy and accelerates learning while simultaneously reducing model uncertainty. We rigorously prove that our active learning algorithm yields a consistent estimate of the underlying dynamics by providing an explicit rate of convergence for the maximum predictive variance. We demonstrate the efficacy of our approach on an under-actuated pendulum system and on the half-cheetah MuJoCo environment.

Refining Human-Centered Autonomy Using Side Information

Data-driven algorithms for human-centered autonomy use observed data to compute models of human behavior in order to ensure safety, correctness, and to avoid potential errors that arise at runtime. However, such algorithms often neglect useful a priori knowledge, known as side information, that can improve the quality of data-driven models. We identify several key challenges in human-centered autonomy, and identify possible approaches to incorporate side information in data-driven models of human behavior.

Physics-Informed Kernel Embeddings: Integrating Prior System Knowledge with Data-Driven Control

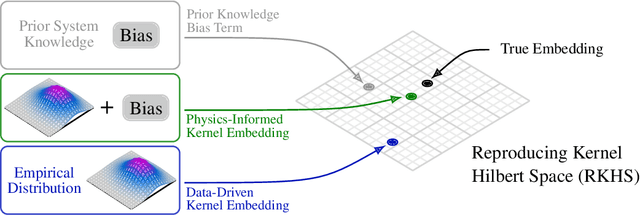
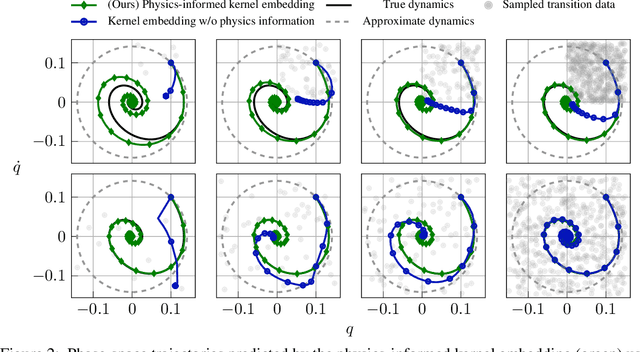
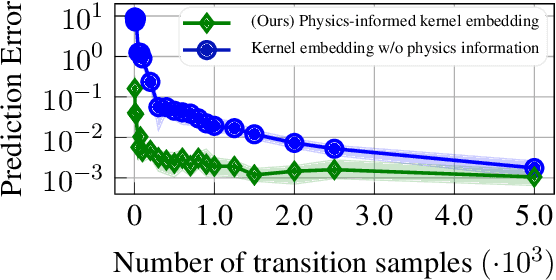
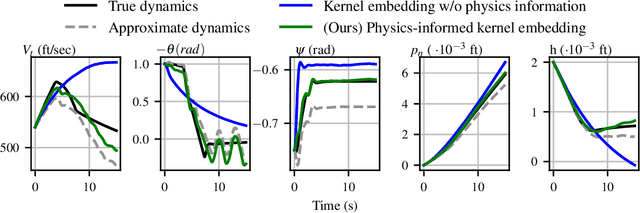
Data-driven control algorithms use observations of system dynamics to construct an implicit model for the purpose of control. However, in practice, data-driven techniques often require excessive sample sizes, which may be infeasible in real-world scenarios where only limited observations of the system are available. Furthermore, purely data-driven methods often neglect useful a priori knowledge, such as approximate models of the system dynamics. We present a method to incorporate such prior knowledge into data-driven control algorithms using kernel embeddings, a nonparametric machine learning technique based in the theory of reproducing kernel Hilbert spaces. Our proposed approach incorporates prior knowledge of the system dynamics as a bias term in the kernel learning problem. We formulate the biased learning problem as a least-squares problem with a regularization term that is informed by the dynamics, that has an efficiently computable, closed-form solution. Through numerical experiments, we empirically demonstrate the improved sample efficiency and out-of-sample generalization of our approach over a purely data-driven baseline. We demonstrate an application of our method to control through a target tracking problem with nonholonomic dynamics, and on spring-mass-damper and F-16 aircraft state prediction tasks.

SOCKS: A Stochastic Optimal Control and Reachability Toolbox Using Kernel Methods

We present SOCKS, a data-driven stochastic optimal control toolbox based in kernel methods. SOCKS is a collection of data-driven algorithms that compute approximate solutions to stochastic optimal control problems with arbitrary cost and constraint functions, including stochastic reachability, which seeks to determine the likelihood that a system will reach a desired target set while respecting a set of pre-defined safety constraints. Our approach relies upon a class of machine learning algorithms based in kernel methods, a nonparametric technique which can be used to represent probability distributions in a high-dimensional space of functions known as a reproducing kernel Hilbert space. As a nonparametric technique, kernel methods are inherently data-driven, meaning that they do not place prior assumptions on the system dynamics or the structure of the uncertainty. This makes the toolbox amenable to a wide variety of systems, including those with nonlinear dynamics, black-box elements, and poorly characterized stochastic disturbances. We present the main features of SOCKS and demonstrate its capabilities on several benchmarks.

Data-Driven Chance Constrained Control using Kernel Distribution Embeddings

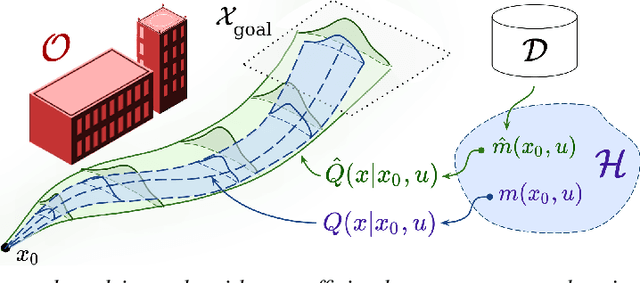
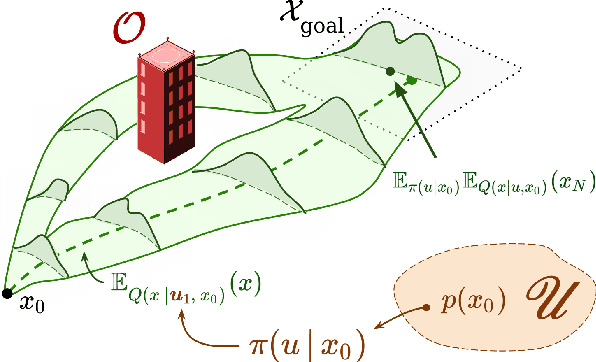
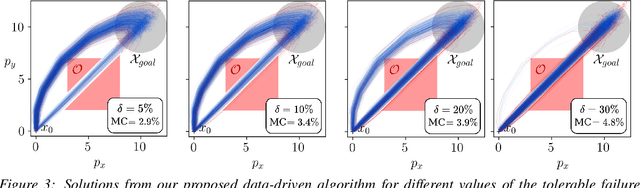
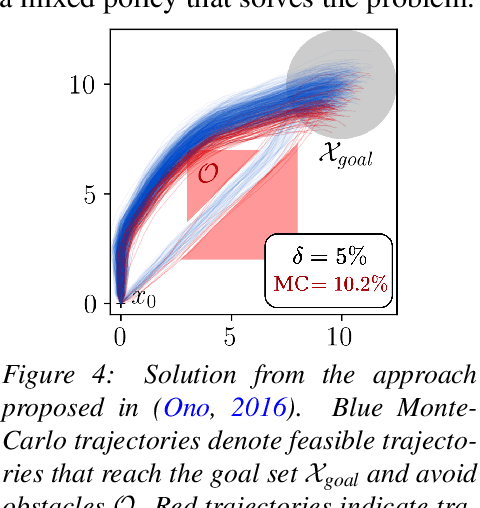
We present a data-driven algorithm for efficiently computing stochastic control policies for general joint chance constrained optimal control problems. Our approach leverages the theory of kernel distribution embeddings, which allows representing expectation operators as inner products in a reproducing kernel Hilbert space. This framework enables approximately reformulating the original problem using a dataset of observed trajectories from the system without imposing prior assumptions on the parameterization of the system dynamics or the structure of the uncertainty. By optimizing over a finite subset of stochastic open-loop control trajectories, we relax the original problem to a linear program over the control parameters that can be efficiently solved using standard convex optimization techniques. We demonstrate our proposed approach in simulation on a system with nonlinear non-Markovian dynamics navigating in a cluttered environment.