Zero-Shot Transfer of Neural ODEs
Paper and Code
May 14, 2024
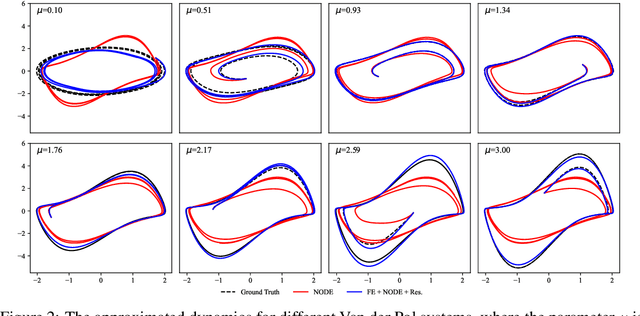
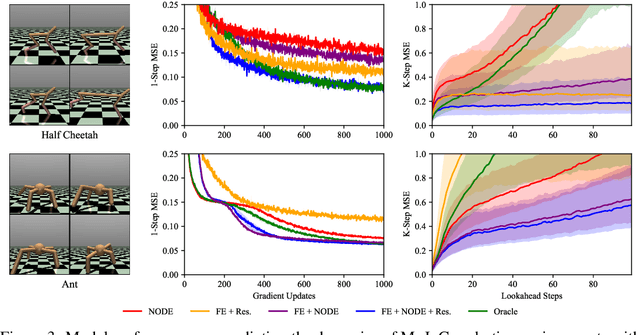
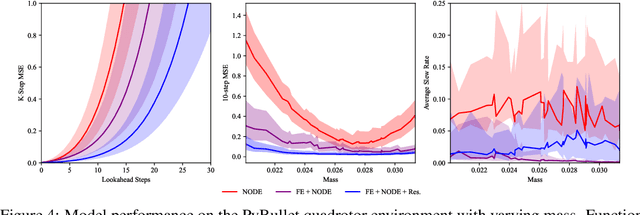
Autonomous systems often encounter environments and scenarios beyond the scope of their training data, which underscores a critical challenge: the need to generalize and adapt to unseen scenarios in real time. This challenge necessitates new mathematical and algorithmic tools that enable adaptation and zero-shot transfer. To this end, we leverage the theory of function encoders, which enables zero-shot transfer by combining the flexibility of neural networks with the mathematical principles of Hilbert spaces. Using this theory, we first present a method for learning a space of dynamics spanned by a set of neural ODE basis functions. After training, the proposed approach can rapidly identify dynamics in the learned space using an efficient inner product calculation. Critically, this calculation requires no gradient calculations or retraining during the online phase. This method enables zero-shot transfer for autonomous systems at runtime and opens the door for a new class of adaptable control algorithms. We demonstrate state-of-the-art system modeling accuracy for two MuJoCo robot environments and show that the learned models can be used for more efficient MPC control of a quadrotor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge