First, Learn What You Don't Know: Active Information Gathering for Driving at the Limits of Handling

Combining data-driven models that adapt online and model predictive control (MPC) has enabled effective control of nonlinear systems. However, when deployed on unstable systems, online adaptation may not be fast enough to ensure reliable simultaneous learning and control. For example, controllers on a vehicle executing highly dynamic maneuvers may push the tires to their friction limits, destabilizing the vehicle and allowing modeling errors to quickly compound and cause a loss of control. In this work, we present a Bayesian meta-learning MPC framework. We propose an expressive vehicle dynamics model that leverages Bayesian last-layer meta-learning to enable rapid online adaptation. The model's uncertainty estimates are used to guide informative data collection and quickly improve the model prior to deployment. Experiments on a Toyota Supra show that (i) the framework enables reliable control in dynamic drifting maneuvers, (ii) online adaptation alone may not suffice for zero-shot control of a vehicle at the edge of stability, and (iii) active data collection helps achieve reliable performance.

Reference-Free Formula Drift with Reinforcement Learning: From Driving Data to Tire Energy-Inspired, Real-World Policies

The skill to drift a car--i.e., operate in a state of controlled oversteer like professional drivers--could give future autonomous cars maximum flexibility when they need to retain control in adverse conditions or avoid collisions. We investigate real-time drifting strategies that put the car where needed while bypassing expensive trajectory optimization. To this end, we design a reinforcement learning agent that builds on the concept of tire energy absorption to autonomously drift through changing and complex waypoint configurations while safely staying within track bounds. We achieve zero-shot deployment on the car by training the agent in a simulation environment built on top of a neural stochastic differential equation vehicle model learned from pre-collected driving data. Experiments on a Toyota GR Supra and Lexus LC 500 show that the agent is capable of drifting smoothly through varying waypoint configurations with tracking error as low as 10 cm while stably pushing the vehicles to sideslip angles of up to 63{\deg}.

Risk-Averse Model Predictive Control for Racing in Adverse Conditions

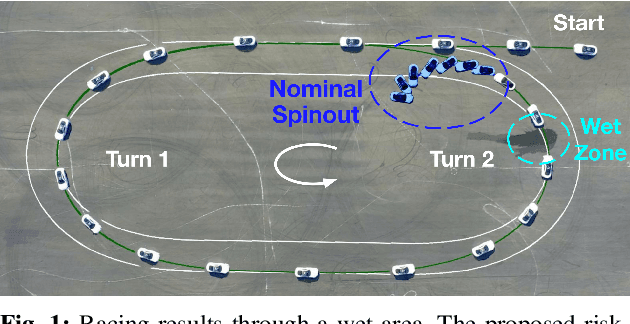
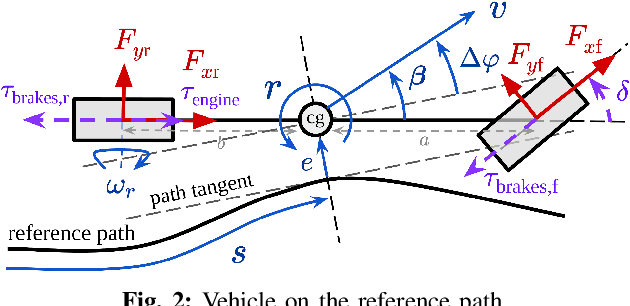
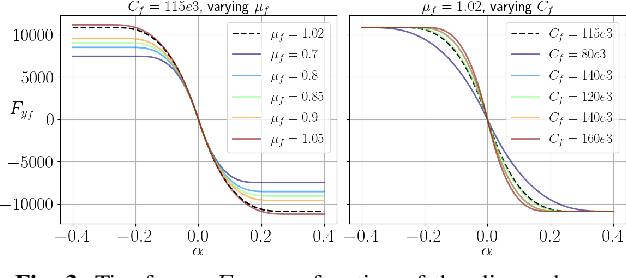
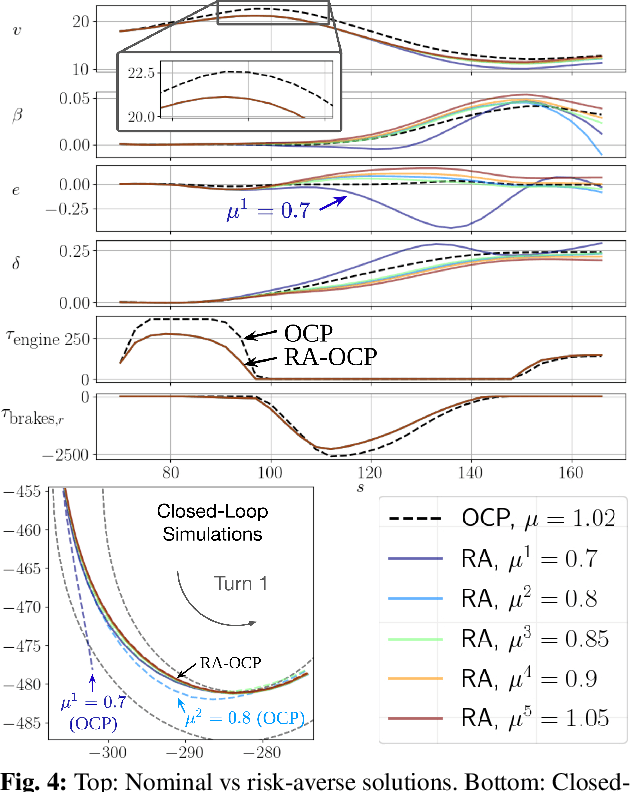
Model predictive control (MPC) algorithms can be sensitive to model mismatch when used in challenging nonlinear control tasks. In particular, the performance of MPC for vehicle control at the limits of handling suffers when the underlying model overestimates the vehicle's capabilities. In this work, we propose a risk-averse MPC framework that explicitly accounts for uncertainty over friction limits and tire parameters. Our approach leverages a sample-based approximation of an optimal control problem with a conditional value at risk (CVaR) constraint. This sample-based formulation enables planning with a set of expressive vehicle dynamics models using different tire parameters. Moreover, this formulation enables efficient numerical resolution via sequential quadratic programming and GPU parallelization. Experiments on a Lexus LC 500 show that risk-averse MPC unlocks reliable performance, while a deterministic baseline that plans using a single dynamics model may lose control of the vehicle in adverse road conditions.

Autonomous Drifting with 3 Minutes of Data via Learned Tire Models

Near the limits of adhesion, the forces generated by a tire are nonlinear and intricately coupled. Efficient and accurate modelling in this region could improve safety, especially in emergency situations where high forces are required. To this end, we propose a novel family of tire force models based on neural ordinary differential equations and a neural-ExpTanh parameterization. These models are designed to satisfy physically insightful assumptions while also having sufficient fidelity to capture higher-order effects directly from vehicle state measurements. They are used as drop-in replacements for an analytical brush tire model in an existing nonlinear model predictive control framework. Experiments with a customized Toyota Supra show that scarce amounts of driving data -- less than three minutes -- is sufficient to achieve high-performance autonomous drifting on various trajectories with speeds up to 45mph. Comparisons with the benchmark model show a $4 \times$ improvement in tracking performance, smoother control inputs, and faster and more consistent computation time.

How to Learn and Generalize From Three Minutes of Data: Physics-Constrained and Uncertainty-Aware Neural Stochastic Differential Equations

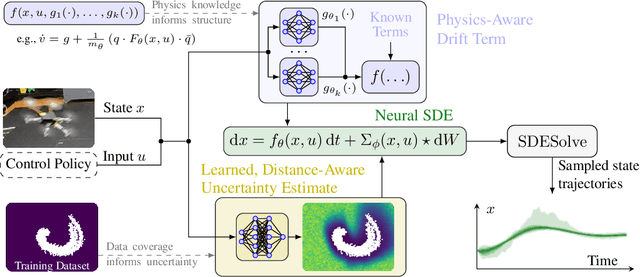
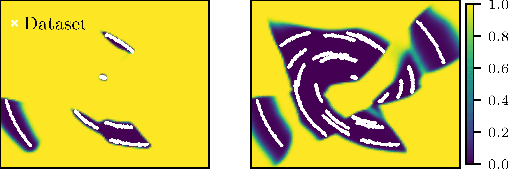
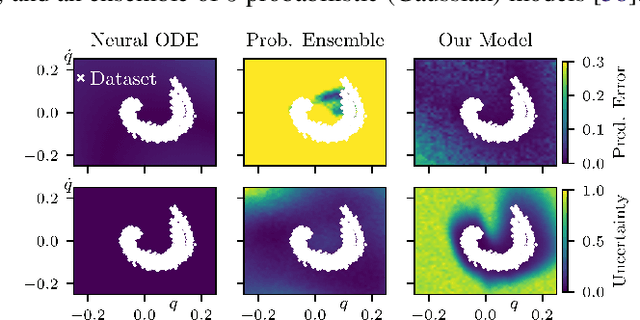
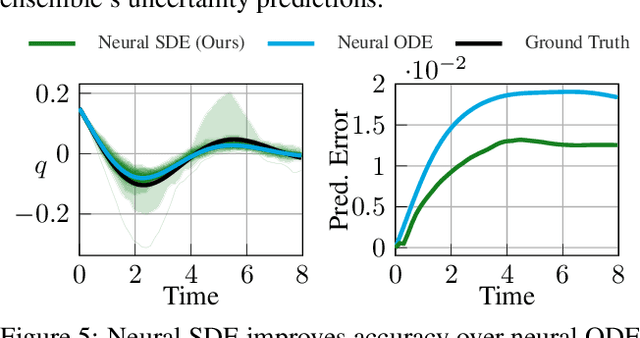
We present a framework and algorithms to learn controlled dynamics models using neural stochastic differential equations (SDEs) -- SDEs whose drift and diffusion terms are both parametrized by neural networks. We construct the drift term to leverage a priori physics knowledge as inductive bias, and we design the diffusion term to represent a distance-aware estimate of the uncertainty in the learned model's predictions -- it matches the system's underlying stochasticity when evaluated on states near those from the training dataset, and it predicts highly stochastic dynamics when evaluated on states beyond the training regime. The proposed neural SDEs can be evaluated quickly enough for use in model predictive control algorithms, or they can be used as simulators for model-based reinforcement learning. Furthermore, they make accurate predictions over long time horizons, even when trained on small datasets that cover limited regions of the state space. We demonstrate these capabilities through experiments on simulated robotic systems, as well as by using them to model and control a hexacopter's flight dynamics: A neural SDE trained using only three minutes of manually collected flight data results in a model-based control policy that accurately tracks aggressive trajectories that push the hexacopter's velocity and Euler angles to nearly double the maximum values observed in the training dataset.

Physics-Informed Kernel Embeddings: Integrating Prior System Knowledge with Data-Driven Control

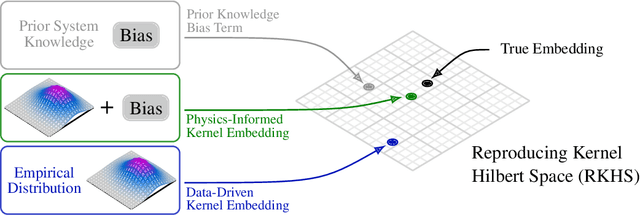
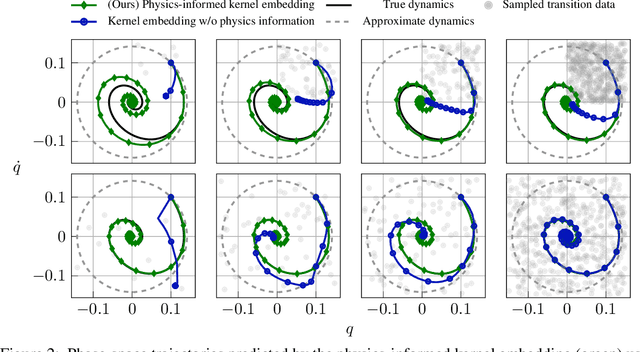
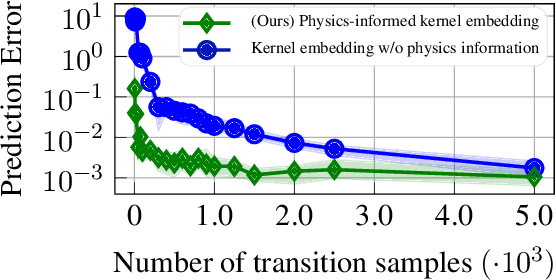
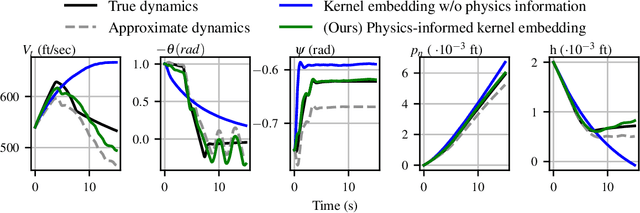
Data-driven control algorithms use observations of system dynamics to construct an implicit model for the purpose of control. However, in practice, data-driven techniques often require excessive sample sizes, which may be infeasible in real-world scenarios where only limited observations of the system are available. Furthermore, purely data-driven methods often neglect useful a priori knowledge, such as approximate models of the system dynamics. We present a method to incorporate such prior knowledge into data-driven control algorithms using kernel embeddings, a nonparametric machine learning technique based in the theory of reproducing kernel Hilbert spaces. Our proposed approach incorporates prior knowledge of the system dynamics as a bias term in the kernel learning problem. We formulate the biased learning problem as a least-squares problem with a regularization term that is informed by the dynamics, that has an efficiently computable, closed-form solution. Through numerical experiments, we empirically demonstrate the improved sample efficiency and out-of-sample generalization of our approach over a purely data-driven baseline. We demonstrate an application of our method to control through a target tracking problem with nonholonomic dynamics, and on spring-mass-damper and F-16 aircraft state prediction tasks.

Task-Guided IRL in POMDPs that Scales

In inverse reinforcement learning (IRL), a learning agent infers a reward function encoding the underlying task using demonstrations from experts. However, many existing IRL techniques make the often unrealistic assumption that the agent has access to full information about the environment. We remove this assumption by developing an algorithm for IRL in partially observable Markov decision processes (POMDPs). We address two limitations of existing IRL techniques. First, they require an excessive amount of data due to the information asymmetry between the expert and the learner. Second, most of these IRL techniques require solving the computationally intractable forward problem -- computing an optimal policy given a reward function -- in POMDPs. The developed algorithm reduces the information asymmetry while increasing the data efficiency by incorporating task specifications expressed in temporal logic into IRL. Such specifications may be interpreted as side information available to the learner a priori in addition to the demonstrations. Further, the algorithm avoids a common source of algorithmic complexity by building on causal entropy as the measure of the likelihood of the demonstrations as opposed to entropy. Nevertheless, the resulting problem is nonconvex due to the so-called forward problem. We solve the intrinsic nonconvexity of the forward problem in a scalable manner through a sequential linear programming scheme that guarantees to converge to a locally optimal policy. In a series of examples, including experiments in a high-fidelity Unity simulator, we demonstrate that even with a limited amount of data and POMDPs with tens of thousands of states, our algorithm learns reward functions and policies that satisfy the task while inducing similar behavior to the expert by leveraging the provided side information.

Taylor-Lagrange Neural Ordinary Differential Equations: Toward Fast Training and Evaluation of Neural ODEs

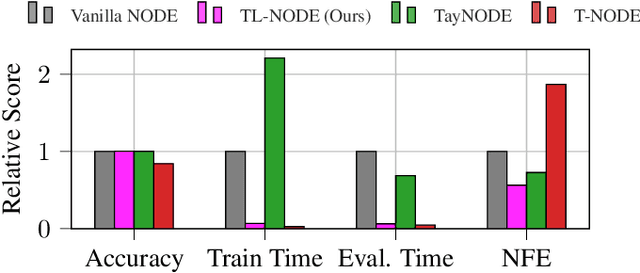
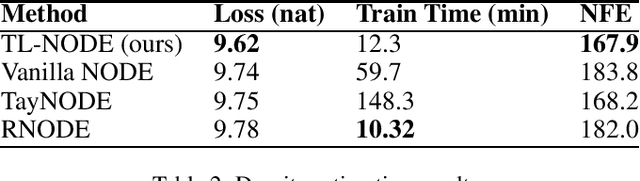
Neural ordinary differential equations (NODEs) -- parametrizations of differential equations using neural networks -- have shown tremendous promise in learning models of unknown continuous-time dynamical systems from data. However, every forward evaluation of a NODE requires numerical integration of the neural network used to capture the system dynamics, making their training prohibitively expensive. Existing works rely on off-the-shelf adaptive step-size numerical integration schemes, which often require an excessive number of evaluations of the underlying dynamics network to obtain sufficient accuracy for training. By contrast, we accelerate the evaluation and the training of NODEs by proposing a data-driven approach to their numerical integration. The proposed Taylor-Lagrange NODEs (TL-NODEs) use a fixed-order Taylor expansion for numerical integration, while also learning to estimate the expansion's approximation error. As a result, the proposed approach achieves the same accuracy as adaptive step-size schemes while employing only low-order Taylor expansions, thus greatly reducing the computational cost necessary to integrate the NODE. A suite of numerical experiments, including modeling dynamical systems, image classification, and density estimation, demonstrate that TL-NODEs can be trained more than an order of magnitude faster than state-of-the-art approaches, without any loss in performance.

Neural Networks with Physics-Informed Architectures and Constraints for Dynamical Systems Modeling

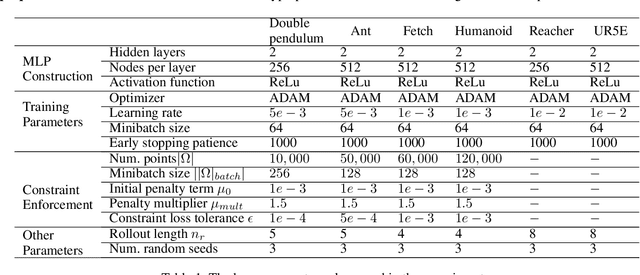
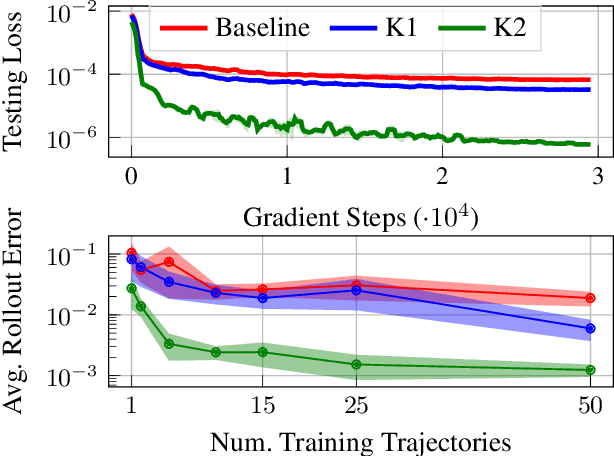
Effective inclusion of physics-based knowledge into deep neural network models of dynamical systems can greatly improve data efficiency and generalization. Such a-priori knowledge might arise from physical principles (e.g., conservation laws) or from the system's design (e.g., the Jacobian matrix of a robot), even if large portions of the system dynamics remain unknown. We develop a framework to learn dynamics models from trajectory data while incorporating a-priori system knowledge as inductive bias. More specifically, the proposed framework uses physics-based side information to inform the structure of the neural network itself, and to place constraints on the values of the outputs and the internal states of the model. It represents the system's vector field as a composition of known and unknown functions, the latter of which are parametrized by neural networks. The physics-informed constraints are enforced via the augmented Lagrangian method during the model's training. We experimentally demonstrate the benefits of the proposed approach on a variety of dynamical systems -- including a benchmark suite of robotics environments featuring large state spaces, non-linear dynamics, external forces, contact forces, and control inputs. By exploiting a-priori system knowledge during training, the proposed approach learns to predict the system dynamics two orders of magnitude more accurately than a baseline approach that does not include prior knowledge, given the same training dataset.

Learning to Reach, Swim, Walk and Fly in One Trial: Data-Driven Control with Scarce Data and Side Information

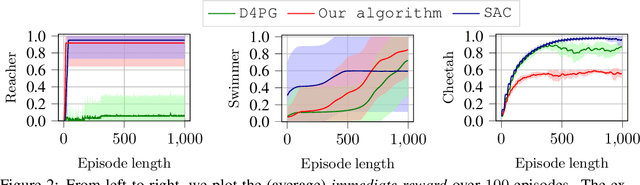
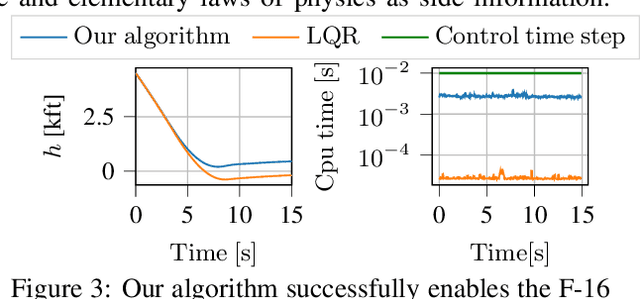
We develop a learning-based control algorithm for unknown dynamical systems under very severe data limitations. Specifically, the algorithm has access to streaming data only from a single and ongoing trial. Despite the scarcity of data, we show -- through a series of examples -- that the algorithm can provide performance comparable to reinforcement learning algorithms trained over millions of environment interactions. It accomplishes such performance by effectively leveraging various forms of side information on the dynamics to reduce the sample complexity. Such side information typically comes from elementary laws of physics and qualitative properties of the system. More precisely, the algorithm approximately solves an optimal control problem encoding the system's desired behavior. To this end, it constructs and refines a differential inclusion that contains the unknown vector field of the dynamics. The differential inclusion, used in an interval Taylor-based method, enables to over-approximate the set of states the system may reach. Theoretically, we establish a bound on the suboptimality of the approximate solution with respect to the case of known dynamics. We show that the longer the trial or the more side information is available, the tighter the bound. Empirically, experiments in a high-fidelity F-16 aircraft simulator and MuJoCo's environments such as the Reacher, Swimmer, and Cheetah illustrate the algorithm's effectiveness.