Learning to Reach, Swim, Walk and Fly in One Trial: Data-Driven Control with Scarce Data and Side Information
Paper and Code
Jun 19, 2021
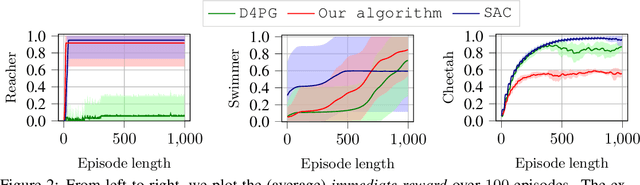
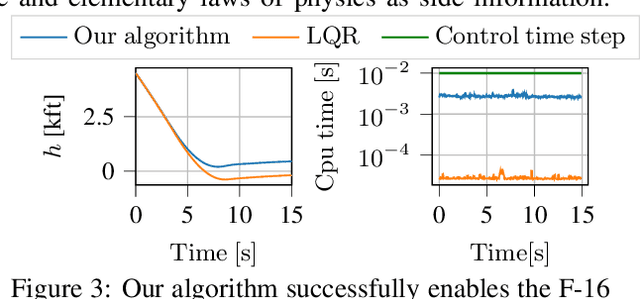
We develop a learning-based control algorithm for unknown dynamical systems under very severe data limitations. Specifically, the algorithm has access to streaming data only from a single and ongoing trial. Despite the scarcity of data, we show -- through a series of examples -- that the algorithm can provide performance comparable to reinforcement learning algorithms trained over millions of environment interactions. It accomplishes such performance by effectively leveraging various forms of side information on the dynamics to reduce the sample complexity. Such side information typically comes from elementary laws of physics and qualitative properties of the system. More precisely, the algorithm approximately solves an optimal control problem encoding the system's desired behavior. To this end, it constructs and refines a differential inclusion that contains the unknown vector field of the dynamics. The differential inclusion, used in an interval Taylor-based method, enables to over-approximate the set of states the system may reach. Theoretically, we establish a bound on the suboptimality of the approximate solution with respect to the case of known dynamics. We show that the longer the trial or the more side information is available, the tighter the bound. Empirically, experiments in a high-fidelity F-16 aircraft simulator and MuJoCo's environments such as the Reacher, Swimmer, and Cheetah illustrate the algorithm's effectiveness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge