Knowledge in multi-robot systems: an interplay of dynamics, computation and communication

We show that the hybrid systems perspective of distributed multi-robot systems is compatible with logical models of knowledge already used in distributed computing, and demonstrate its usefulness by deriving sufficient epistemic conditions for exploration and gathering robot tasks to be solvable. We provide a separation of the physical and computational aspects of a robotic system, allowing us to decouple the problems related to each and directly use methods from control theory and distributed computing, fields that are traditionally distant in the literature. Finally, we demonstrate a novel approach for reasoning about the knowledge in multi-robot systems through a principled method of converting a switched hybrid dynamical system into a temporal-epistemic logic model, passing through an abstract state machine representation. This creates space for methods and results to be exchanged across the fields of control theory, distributed computing and temporal-epistemic logic, while reasoning about multi-robot systems.

Simplicial Models for the Epistemic Logic of Faulty Agents

In recent years, several authors have been investigating simplicial models, a model of epistemic logic based on higher-dimensional structures called simplicial complexes. In the original formulation, simplicial models were always assumed to be pure, meaning that all worlds have the same dimension. This is equivalent to the standard S5n semantics of epistemic logic, based on Kripke models. By removing the assumption that models must be pure, we can go beyond the usual Kripke semantics and study epistemic logics where the number of agents participating in a world can vary. This approach has been developed in a number of papers, with applications in fault-tolerant distributed computing where processes may crash during the execution of a system. A difficulty that arises is that subtle design choices in the definition of impure simplicial models can result in different axioms of the resulting logic. In this paper, we classify those design choices systematically, and axiomatize the corresponding logics. We illustrate them via distributed computing examples of synchronous systems where processes may crash.

Estimating the Coverage Measure and the Area Explored by a Line-Sweep Sensor on the Plane

This paper presents a method for determining the area explored by a line-sweep sensor during an area-covering mission in a two-dimensional plane. Accurate knowledge of the explored area is crucial for various applications in robotics, such as mapping, surveillance, and coverage optimization. The proposed method leverages the concept of coverage measure of the environment and its relation to the topological degree in the plane, to estimate the extent of the explored region. In addition, we extend the approach to uncertain coverage measure values using interval analysis. This last contribution allows for a guaranteed characterization of the explored area, essential considering the often critical character of area-covering missions. Finally, this paper also proposes a novel algorithm for computing the topological degree in the 2-dimensional plane, for all the points inside an area of interest, which differs from existing solutions that compute the topological degree for single points. The applicability of the method is evaluated through a real-world experiment.

Taylor-Lagrange Neural Ordinary Differential Equations: Toward Fast Training and Evaluation of Neural ODEs

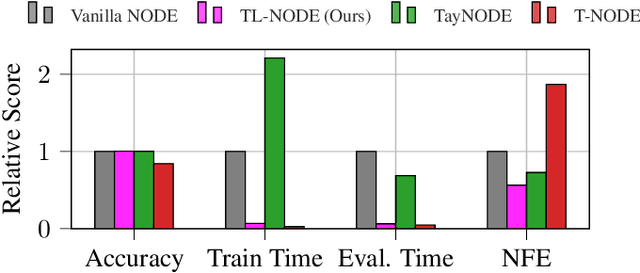
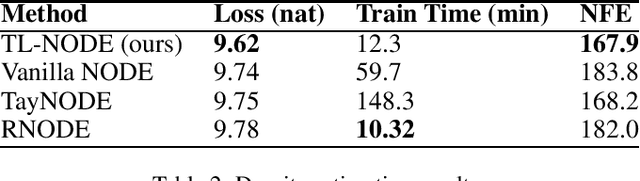
Neural ordinary differential equations (NODEs) -- parametrizations of differential equations using neural networks -- have shown tremendous promise in learning models of unknown continuous-time dynamical systems from data. However, every forward evaluation of a NODE requires numerical integration of the neural network used to capture the system dynamics, making their training prohibitively expensive. Existing works rely on off-the-shelf adaptive step-size numerical integration schemes, which often require an excessive number of evaluations of the underlying dynamics network to obtain sufficient accuracy for training. By contrast, we accelerate the evaluation and the training of NODEs by proposing a data-driven approach to their numerical integration. The proposed Taylor-Lagrange NODEs (TL-NODEs) use a fixed-order Taylor expansion for numerical integration, while also learning to estimate the expansion's approximation error. As a result, the proposed approach achieves the same accuracy as adaptive step-size schemes while employing only low-order Taylor expansions, thus greatly reducing the computational cost necessary to integrate the NODE. A suite of numerical experiments, including modeling dynamical systems, image classification, and density estimation, demonstrate that TL-NODEs can be trained more than an order of magnitude faster than state-of-the-art approaches, without any loss in performance.

Neural Networks with Physics-Informed Architectures and Constraints for Dynamical Systems Modeling

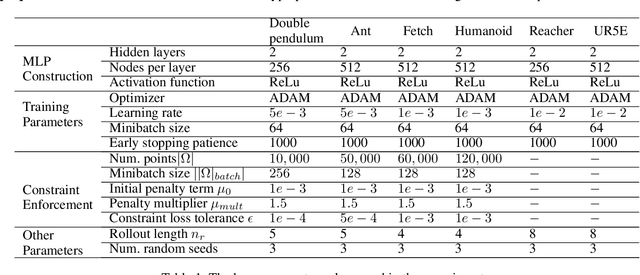
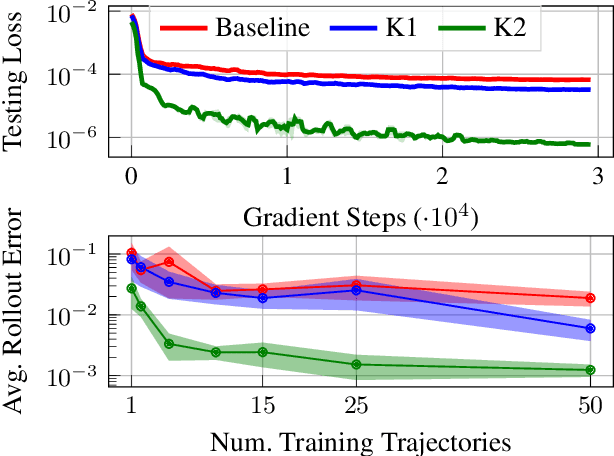
Effective inclusion of physics-based knowledge into deep neural network models of dynamical systems can greatly improve data efficiency and generalization. Such a-priori knowledge might arise from physical principles (e.g., conservation laws) or from the system's design (e.g., the Jacobian matrix of a robot), even if large portions of the system dynamics remain unknown. We develop a framework to learn dynamics models from trajectory data while incorporating a-priori system knowledge as inductive bias. More specifically, the proposed framework uses physics-based side information to inform the structure of the neural network itself, and to place constraints on the values of the outputs and the internal states of the model. It represents the system's vector field as a composition of known and unknown functions, the latter of which are parametrized by neural networks. The physics-informed constraints are enforced via the augmented Lagrangian method during the model's training. We experimentally demonstrate the benefits of the proposed approach on a variety of dynamical systems -- including a benchmark suite of robotics environments featuring large state spaces, non-linear dynamics, external forces, contact forces, and control inputs. By exploiting a-priori system knowledge during training, the proposed approach learns to predict the system dynamics two orders of magnitude more accurately than a baseline approach that does not include prior knowledge, given the same training dataset.

A Simplicial Model for $KB4_n$: Epistemic Logic with Agents that May Die

The standard semantics of multi-agent epistemic logic $S5$ is based on Kripke models whose accessibility relations are reflexive, symmetric and transitive. This one dimensional structure contains implicit higher-dimensional information beyond pairwise interactions, that has been formalized as pure simplicial models in previous work from the authors. Here we extend the theory to encompass all simplicial models - including the ones that are not pure. The corresponding Kripke models are those where the accessibility relation is symmetric and transitive, but might not be reflexive. This yields the epistemic logic $KB4$ which can reason about situations where some of the agents may die.

Static analysis of ReLU neural networks with tropical polyhedra

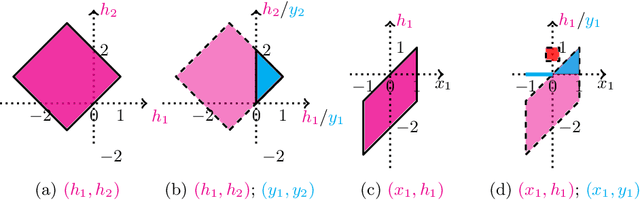
This paper studies the problem of range analysis for feedforward neural networks, which is a basic primitive for applications such as robustness of neural networks, compliance to specifications and reachability analysis of neural-network feedback systems. Our approach focuses on ReLU (rectified linear unit) feedforward neural nets that present specific difficulties: approaches that exploit derivatives do not apply in general, the number of patterns of neuron activations can be quite large even for small networks, and convex approximations are generally too coarse. In this paper, we employ set-based methods and abstract interpretation that have been very successful in coping with similar difficulties in classical program verification. We present an approach that abstracts ReLU feedforward neural networks using tropical polyhedra. We show that tropical polyhedra can efficiently abstract ReLU activation function, while being able to control the loss of precision due to linear computations. We show how the connection between ReLU networks and tropical rational functions can provide approaches for range analysis of ReLU neural networks.

Neural Network Based Model Predictive Control for an Autonomous Vehicle

We study learning based controllers as a replacement for model predictive controllers (MPC) for the control of autonomous vehicles. We concentrate for the experiments on the simple yet representative bicycle model. We compare training by supervised learning and by reinforcement learning. We also discuss the neural net architectures so as to obtain small nets with the best performances. This work aims at producing controllers that can both be embedded on real-time platforms and amenable to verification by formal methods techniques.

Reinforcement Learning with Formal Performance Metrics for Quadcopter Attitude Control under Non-nominal Contexts

We explore the reinforcement learning approach to designing controllers by extensively discussing the case of a quadcopter attitude controller. We provide all details allowing to reproduce our approach, starting with a model of the dynamics of a crazyflie 2.0 under various nominal and non-nominal conditions, including partial motor failures and wind gusts. We develop a robust form of a signal temporal logic to quantitatively evaluate the vehicle's behavior and measure the performance of controllers. The paper thoroughly describes the choices in training algorithms, neural net architecture, hyperparameters, observation space in view of the different performance metrics we have introduced. We discuss the robustness of the obtained controllers, both to partial loss of power for one rotor and to wind gusts and finish by drawing conclusions on practical controller design by reinforcement learning.

Formal Verification of Station Keeping Maneuvers for a Planar Autonomous Hybrid System

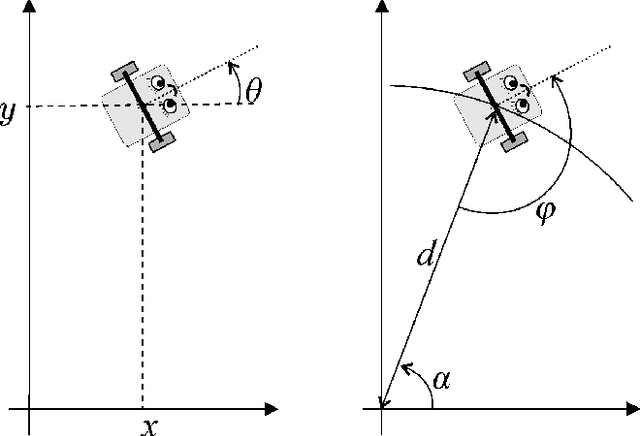
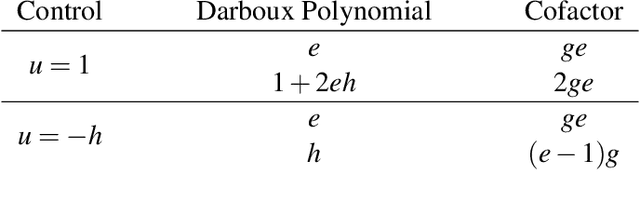
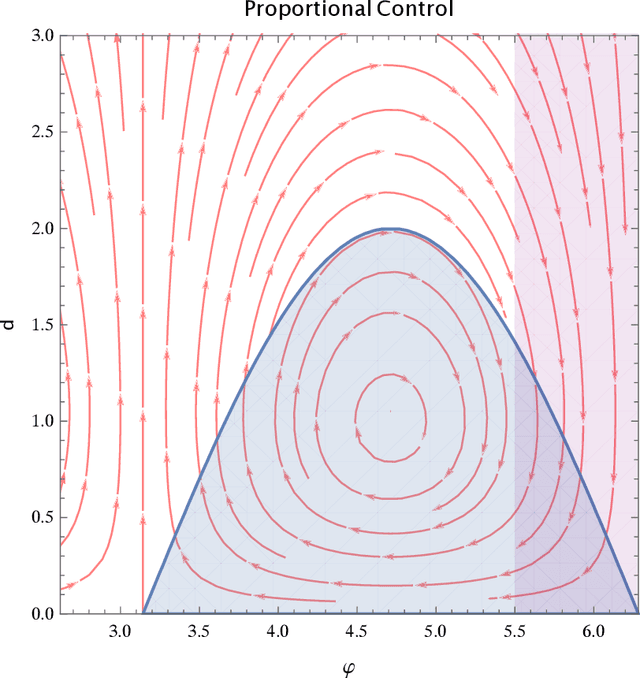
We formally verify a hybrid control law designed to perform a station keeping maneuver for a planar vehicle. Such maneuver requires that the vehicle reaches a neighborhood of its station in finite time and remains in it while waiting for further instructions. We model the dynamics as well as the control law as a hybrid program and formally verify both the reachability and safety properties involved. We highlight in particular the automated generation of invariant regions which turns out to be crucial in performing such verification. We use the theorem prover Keymaera X to discharge some of the generated proof obligations.