A Machine Learning-based Approach for Solving Recurrence Relations and its use in Cost Analysis of Logic Programs

Automatic static cost analysis infers information about the resources used by programs without actually running them with concrete data, and presents such information as functions of input data sizes. Most of the analysis tools for logic programs (and many for other languages), as CiaoPP, are based on setting up recurrence relations representing (bounds on) the computational cost of predicates, and solving them to find closed-form functions. Such recurrence solving is a bottleneck in current tools: many of the recurrences that arise during the analysis cannot be solved with state-of-the-art solvers, including Computer Algebra Systems (CASs), so that specific methods for different classes of recurrences need to be developed. We address such a challenge by developing a novel, general approach for solving arbitrary, constrained recurrence relations, that uses machine-learning (sparse-linear and symbolic) regression techniques to guess a candidate closed-form function, and a combination of an SMT-solver and a CAS to check if it is actually a solution of the recurrence. Our prototype implementation and its experimental evaluation within the context of the CiaoPP system show quite promising results. Overall, for the considered benchmarks, our approach outperforms state-of-the-art cost analyzers and recurrence solvers, and solves recurrences that cannot be solved by them.

Static analysis of ReLU neural networks with tropical polyhedra

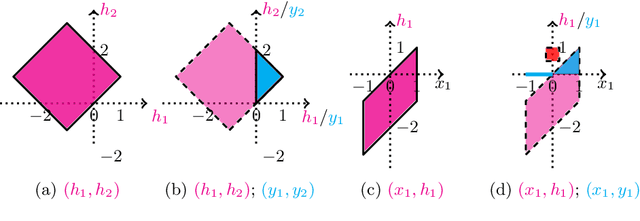
This paper studies the problem of range analysis for feedforward neural networks, which is a basic primitive for applications such as robustness of neural networks, compliance to specifications and reachability analysis of neural-network feedback systems. Our approach focuses on ReLU (rectified linear unit) feedforward neural nets that present specific difficulties: approaches that exploit derivatives do not apply in general, the number of patterns of neuron activations can be quite large even for small networks, and convex approximations are generally too coarse. In this paper, we employ set-based methods and abstract interpretation that have been very successful in coping with similar difficulties in classical program verification. We present an approach that abstracts ReLU feedforward neural networks using tropical polyhedra. We show that tropical polyhedra can efficiently abstract ReLU activation function, while being able to control the loss of precision due to linear computations. We show how the connection between ReLU networks and tropical rational functions can provide approaches for range analysis of ReLU neural networks.