Ordered Functional Decision Diagrams

Several BDD variants were designed to exploit special features of Boolean functions to achieve better compression rates.Deciding a priori which variant to use is as hard as constructing the diagrams themselves and the conversion between variants comes in general with a prohibitive cost.This observation leads naturally to a growing interest into when and how one can combine existing variants to benefit from their respective sweet spots.In this paper, we introduce a novel framework, termed \lambdaDD (LDD), that revisits BDD from a purely functional point of view.The framework allows to classify the already existing variants, including the most recent ones like ChainDD and ESRBDD, as implementations of a special class of ordered models.We enumerate, in a principled way, all the models of this class and isolate its most expressive model.This new model, termed \lambdaDD-O-NUCX, is suitable for both dense and sparse Boolean functions, and, unlike ChainDD and ESRBDD, is invariant by negation.The canonicity of \lambdaDD-O-NUCX is formally verified using the Coq proof assistant.We furthermore provide experimental evidence corroborating our theoretical findings: more expressive \lambdaDD models achieve, indeed, better memory compression rates.

Formal Verification of Station Keeping Maneuvers for a Planar Autonomous Hybrid System

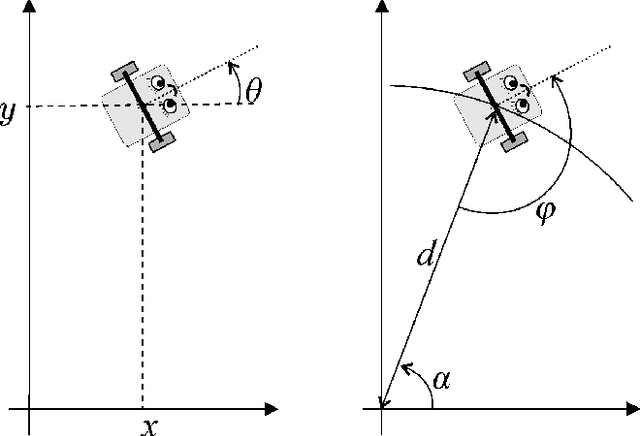
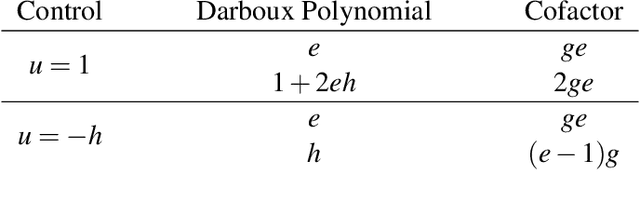
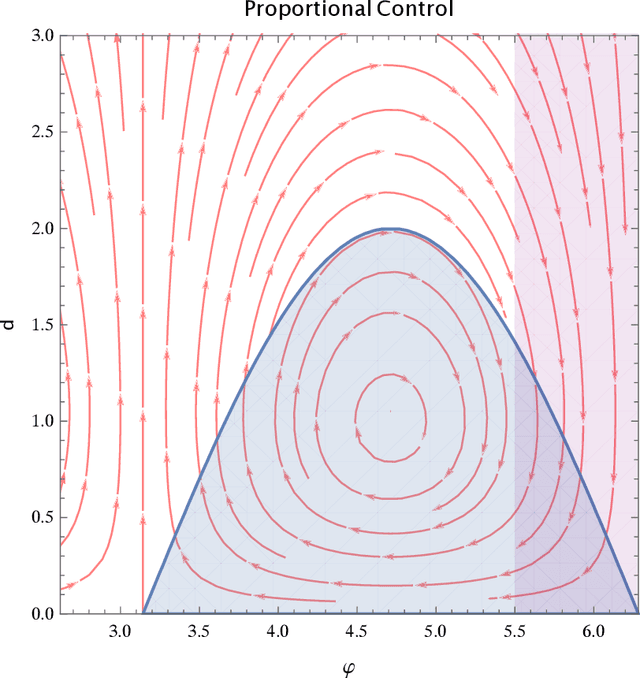
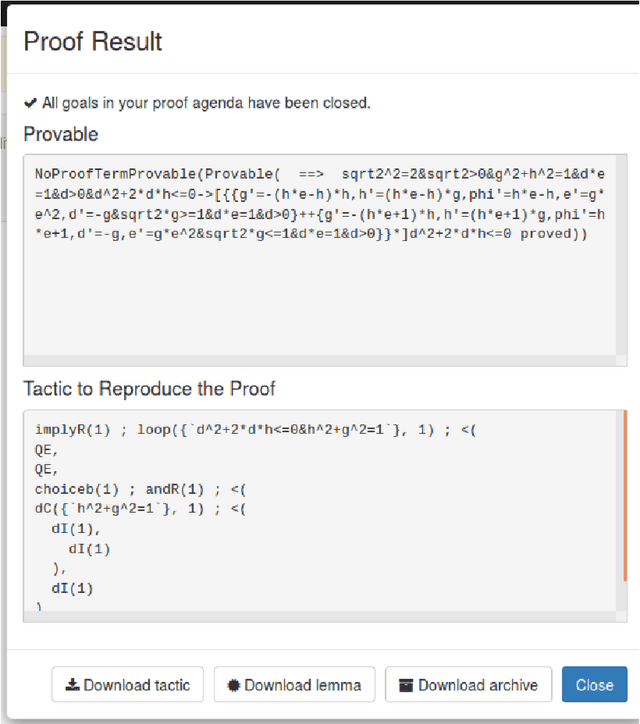
We formally verify a hybrid control law designed to perform a station keeping maneuver for a planar vehicle. Such maneuver requires that the vehicle reaches a neighborhood of its station in finite time and remains in it while waiting for further instructions. We model the dynamics as well as the control law as a hybrid program and formally verify both the reachability and safety properties involved. We highlight in particular the automated generation of invariant regions which turns out to be crucial in performing such verification. We use the theorem prover Keymaera X to discharge some of the generated proof obligations.

Formal Verification of Obstacle Avoidance and Navigation of Ground Robots

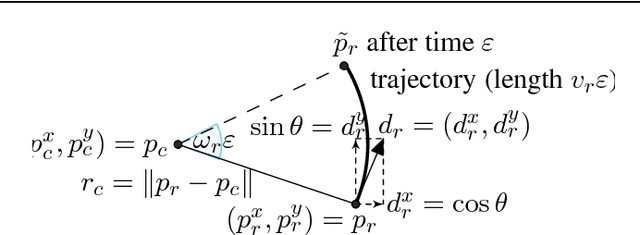
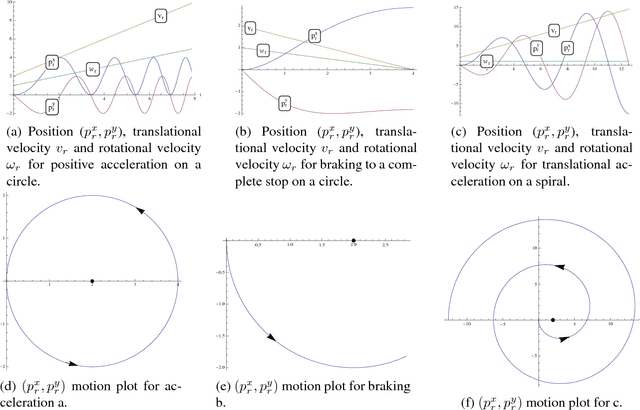
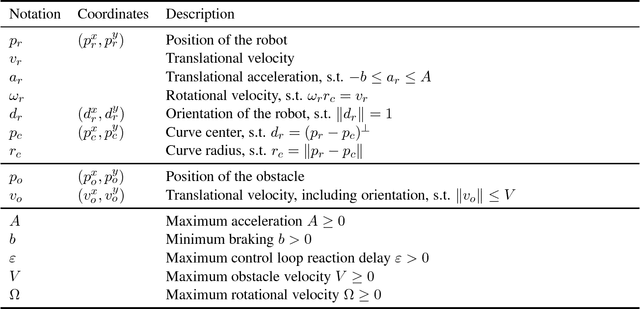
The safety of mobile robots in dynamic environments is predicated on making sure that they do not collide with obstacles. In support of such safety arguments, we analyze and formally verify a series of increasingly powerful safety properties of controllers for avoiding both stationary and moving obstacles: (i) static safety, which ensures that no collisions can happen with stationary obstacles, (ii) passive safety, which ensures that no collisions can happen with stationary or moving obstacles while the robot moves, (iii) the stronger passive friendly safety in which the robot further maintains sufficient maneuvering distance for obstacles to avoid collision as well, and (iv) passive orientation safety, which allows for imperfect sensor coverage of the robot, i. e., the robot is aware that not everything in its environment will be visible. We complement these provably correct safety properties with liveness properties: we prove that provably safe motion is flexible enough to let the robot still navigate waypoints and pass intersections. We use hybrid system models and theorem proving techniques that describe and formally verify the robot's discrete control decisions along with its continuous, physical motion. Moreover, we formally prove that safety can still be guaranteed despite sensor uncertainty and actuator perturbation, and when control choices for more aggressive maneuvers are introduced. Our verification results are generic in the sense that they are not limited to the particular choices of one specific control algorithm but identify conditions that make them simultaneously apply to a broad class of control algorithms.