Provably Safe Neural Network Controllers via Differential Dynamic Logic

While neural networks (NNs) have a large potential as goal-oriented controllers for Cyber-Physical Systems, verifying the safety of neural network based control systems (NNCSs) poses significant challenges for the practical use of NNs -- especially when safety is needed for unbounded time horizons. One reason for this is the intractability of NN and hybrid system analysis. We introduce VerSAILLE (Verifiably Safe AI via Logically Linked Envelopes): The first approach for the combination of differential dynamic logic (dL) and NN verification. By joining forces, we can exploit the efficiency of NN verification tools while retaining the rigor of dL. We reflect a safety proof for a controller envelope in an NN to prove the safety of concrete NNCS on an infinite-time horizon. The NN verification properties resulting from VerSAILLE typically require nonlinear arithmetic while efficient NN verification tools merely support linear arithmetic. To overcome this divide, we present Mosaic: The first sound and complete verification approach for polynomial real arithmetic properties on piece-wise linear NNs. Mosaic lifts off-the-shelf tools for linear properties to the nonlinear setting. An evaluation on case studies, including adaptive cruise control and airborne collision avoidance, demonstrates the versatility of VerSAILLE and Mosaic: It supports the certification of infinite-time horizon safety and the exhaustive enumeration of counterexample regions while significantly outperforming State-of-the-Art tools in closed-loop NNV.

Fanoos: Multi-Resolution, Multi-Strength, Interactive Explanations for Learned Systems

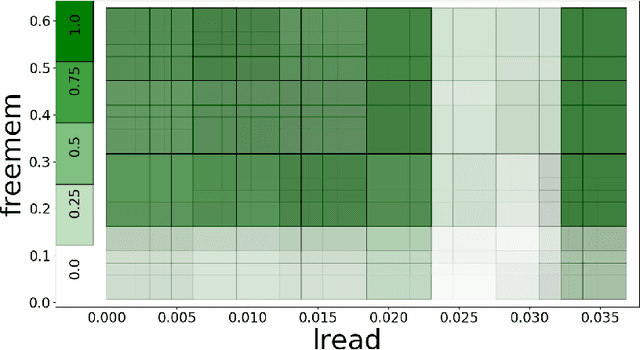
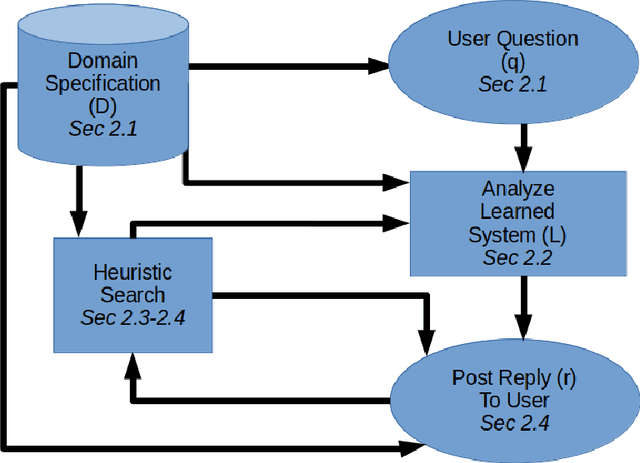
Machine learning becomes increasingly important to tune or even synthesize the behavior of safety-critical components in highly non-trivial environments, where the inability to understand learned components in general, and neural nets in particular, poses serious obstacles to their adoption. Explainability and interpretability methods for learned systems have gained considerable academic attention, but the focus of current approaches on only one aspect of explanation, at a fixed level of abstraction, and limited if any formal guarantees, prevents those explanations from being digestible by the relevant stakeholders (e.g., end users, certification authorities, engineers) with their diverse backgrounds and situation-specific needs. We introduce Fanoos, a flexible framework for combining formal verification techniques, heuristic search, and user interaction to explore explanations at the desired level of granularity and fidelity. We demonstrate the ability of Fanoos to produce and adjust the abstractness of explanations in response to user requests on a learned controller for an inverted double pendulum and on a learned CPU usage model.

Blackbox End-to-End Verification of Ground Robot Safety and Liveness

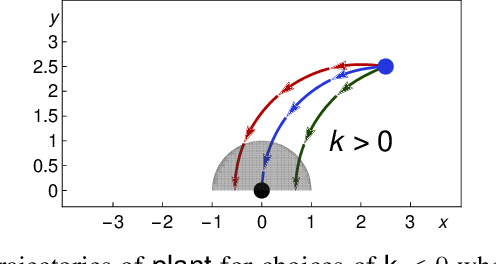
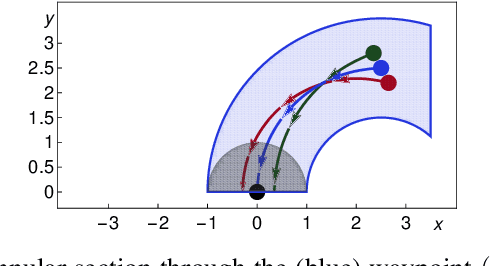
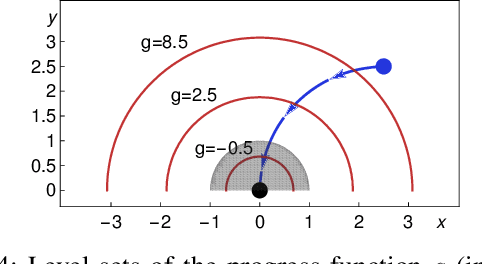
We formally prove end-to-end correctness of a ground robot implemented in a simulator. We use an untrusted controller supervised by a verified sandbox. Contributions include: (i) A model of the robot in differential dynamic logic, which specifies assumptions on the controller and robot kinematics, (ii) Formal proofs of safety and liveness for a waypoint-following problem with speed limits, (iii) An automatically synthesized sandbox, which is automatically proven to enforce model compliance at runtime, and (iv) Controllers, planners, and environments for the simulations. The verified sandbox is used to safeguard (unverified) controllers in a realistic simulated environment. Experimental evaluation of the resulting sandboxed implementation confirms safety and high model-compliance, with an inherent trade-off between compliance and performance. The verified sandbox thus serves as a valuable bidirectional link between formal methods and implementation, automating both enforcement of safety and model validation simultaneously.

Formal Verification of Obstacle Avoidance and Navigation of Ground Robots

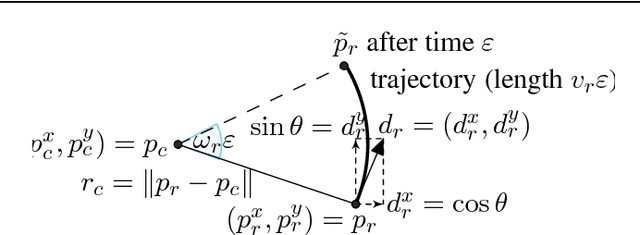
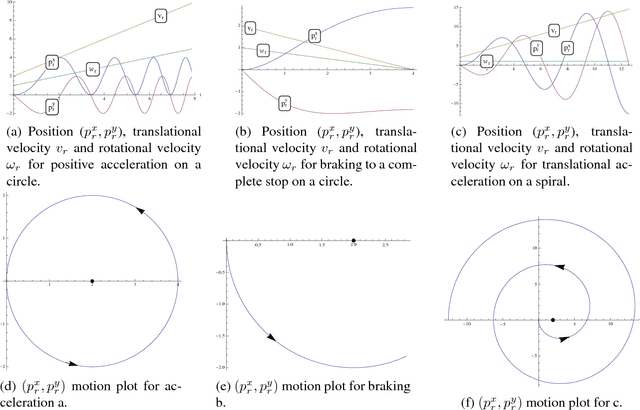
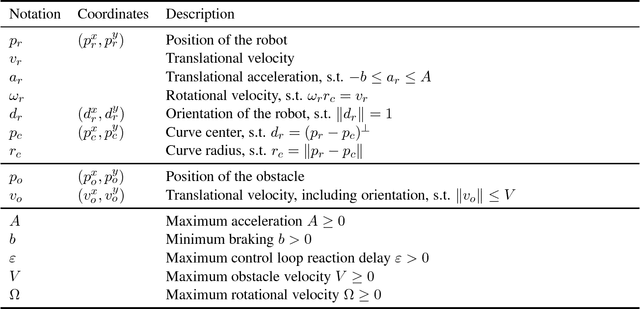
The safety of mobile robots in dynamic environments is predicated on making sure that they do not collide with obstacles. In support of such safety arguments, we analyze and formally verify a series of increasingly powerful safety properties of controllers for avoiding both stationary and moving obstacles: (i) static safety, which ensures that no collisions can happen with stationary obstacles, (ii) passive safety, which ensures that no collisions can happen with stationary or moving obstacles while the robot moves, (iii) the stronger passive friendly safety in which the robot further maintains sufficient maneuvering distance for obstacles to avoid collision as well, and (iv) passive orientation safety, which allows for imperfect sensor coverage of the robot, i. e., the robot is aware that not everything in its environment will be visible. We complement these provably correct safety properties with liveness properties: we prove that provably safe motion is flexible enough to let the robot still navigate waypoints and pass intersections. We use hybrid system models and theorem proving techniques that describe and formally verify the robot's discrete control decisions along with its continuous, physical motion. Moreover, we formally prove that safety can still be guaranteed despite sensor uncertainty and actuator perturbation, and when control choices for more aggressive maneuvers are introduced. Our verification results are generic in the sense that they are not limited to the particular choices of one specific control algorithm but identify conditions that make them simultaneously apply to a broad class of control algorithms.