Revisiting Differential Verification: Equivalence Verification with Confidence

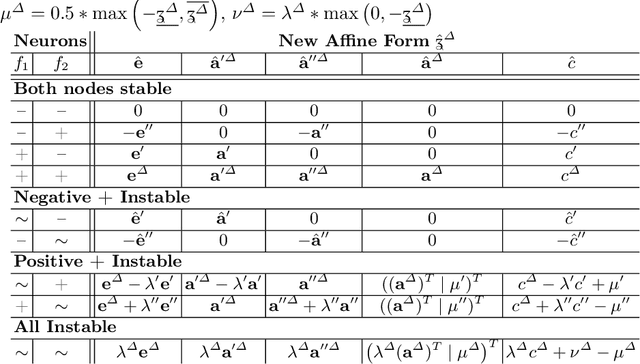
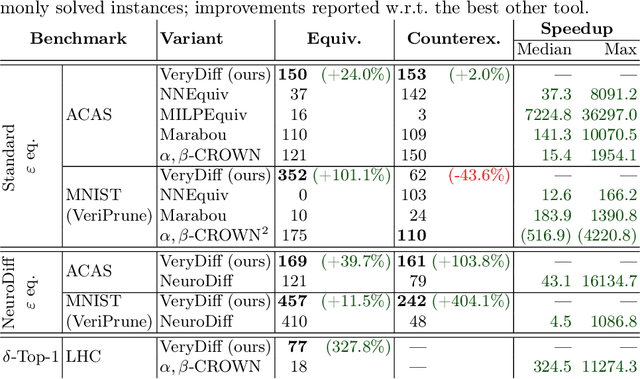
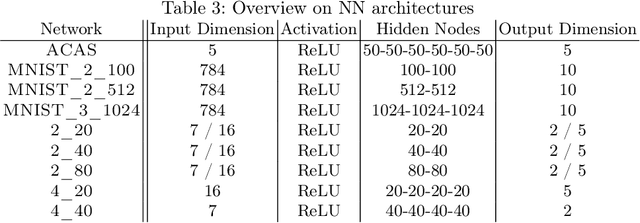
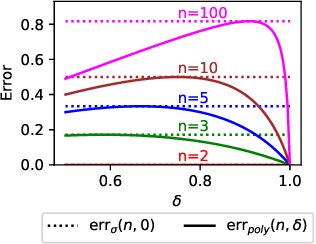
When validated neural networks (NNs) are pruned (and retrained) before deployment, it is desirable to prove that the new NN behaves equivalently to the (original) reference NN. To this end, our paper revisits the idea of differential verification which performs reasoning on differences between NNs: On the one hand, our paper proposes a novel abstract domain for differential verification admitting more efficient reasoning about equivalence. On the other hand, we investigate empirically and theoretically which equivalence properties are (not) efficiently solved using differential reasoning. Based on the gained insights, and following a recent line of work on confidence-based verification, we propose a novel equivalence property that is amenable to Differential Verification while providing guarantees for large parts of the input space instead of small-scale guarantees constructed w.r.t. predetermined input points. We implement our approach in a new tool called VeryDiff and perform an extensive evaluation on numerous old and new benchmark families, including new pruned NNs for particle jet classification in the context of CERN's LHC where we observe median speedups >300x over the State-of-the-Art verifier alpha,beta-CROWN.

Provably Safe Neural Network Controllers via Differential Dynamic Logic

While neural networks (NNs) have a large potential as goal-oriented controllers for Cyber-Physical Systems, verifying the safety of neural network based control systems (NNCSs) poses significant challenges for the practical use of NNs -- especially when safety is needed for unbounded time horizons. One reason for this is the intractability of NN and hybrid system analysis. We introduce VerSAILLE (Verifiably Safe AI via Logically Linked Envelopes): The first approach for the combination of differential dynamic logic (dL) and NN verification. By joining forces, we can exploit the efficiency of NN verification tools while retaining the rigor of dL. We reflect a safety proof for a controller envelope in an NN to prove the safety of concrete NNCS on an infinite-time horizon. The NN verification properties resulting from VerSAILLE typically require nonlinear arithmetic while efficient NN verification tools merely support linear arithmetic. To overcome this divide, we present Mosaic: The first sound and complete verification approach for polynomial real arithmetic properties on piece-wise linear NNs. Mosaic lifts off-the-shelf tools for linear properties to the nonlinear setting. An evaluation on case studies, including adaptive cruise control and airborne collision avoidance, demonstrates the versatility of VerSAILLE and Mosaic: It supports the certification of infinite-time horizon safety and the exhaustive enumeration of counterexample regions while significantly outperforming State-of-the-Art tools in closed-loop NNV.

An Information-Flow Perspective on Algorithmic Fairness

This work presents insights gained by investigating the relationship between algorithmic fairness and the concept of secure information flow. The problem of enforcing secure information flow is well-studied in the context of information security: If secret information may "flow" through an algorithm or program in such a way that it can influence the program's output, then that is considered insecure information flow as attackers could potentially observe (parts of) the secret. There is a strong correspondence between secure information flow and algorithmic fairness: if protected attributes such as race, gender, or age are treated as secret program inputs, then secure information flow means that these ``secret'' attributes cannot influence the result of a program. While most research in algorithmic fairness evaluation concentrates on studying the impact of algorithms (often treating the algorithm as a black-box), the concepts derived from information flow can be used both for the analysis of disparate treatment as well as disparate impact w.r.t. a structural causal model. In this paper, we examine the relationship between quantitative as well as qualitative information-flow properties and fairness. Moreover, based on this duality, we derive a new quantitative notion of fairness called fairness spread, which can be easily analyzed using quantitative information flow and which strongly relates to counterfactual fairness. We demonstrate that off-the-shelf tools for information-flow properties can be used in order to formally analyze a program's algorithmic fairness properties, including the new notion of fairness spread as well as established notions such as demographic parity.

Geometric Path Enumeration for Equivalence Verification of Neural Networks

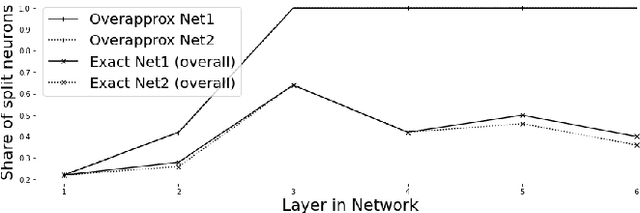
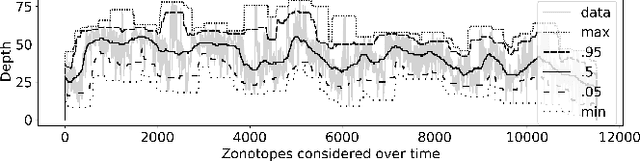
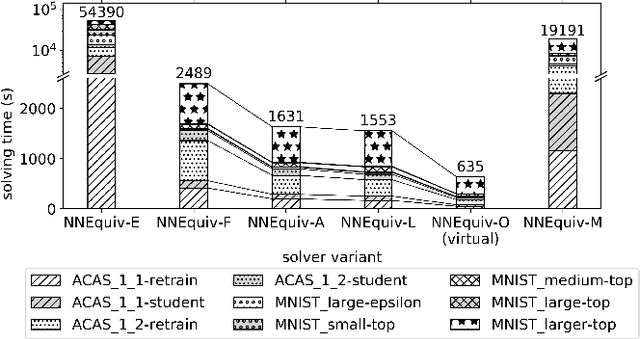
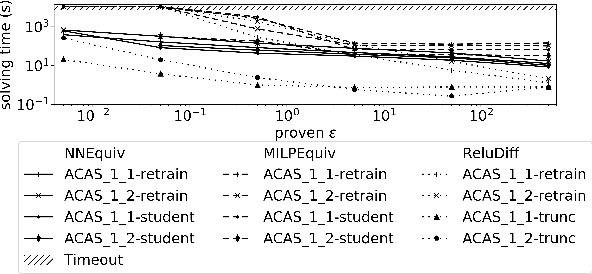
As neural networks (NNs) are increasingly introduced into safety-critical domains, there is a growing need to formally verify NNs before deployment. In this work we focus on the formal verification problem of NN equivalence which aims to prove that two NNs (e.g. an original and a compressed version) show equivalent behavior. Two approaches have been proposed for this problem: Mixed integer linear programming and interval propagation. While the first approach lacks scalability, the latter is only suitable for structurally similar NNs with small weight changes. The contribution of our paper has four parts. First, we show a theoretical result by proving that the epsilon-equivalence problem is coNP-complete. Secondly, we extend Tran et al.'s single NN geometric path enumeration algorithm to a setting with multiple NNs. In a third step, we implement the extended algorithm for equivalence verification and evaluate optimizations necessary for its practical use. Finally, we perform a comparative evaluation showing use-cases where our approach outperforms the previous state of the art, both, for equivalence verification as well as for counter-example finding.