Optimized Symbolic Interval Propagation for Neural Network Verification

Neural networks are increasingly applied in safety critical domains, their verification thus is gaining importance. A large class of recent algorithms for proving input-output relations of feed-forward neural networks are based on linear relaxations and symbolic interval propagation. However, due to variable dependencies, the approximations deteriorate with increasing depth of the network. In this paper we present DPNeurifyFV, a novel branch-and-bound solver for ReLU networks with low dimensional input-space that is based on symbolic interval propagation with fresh variables and input-splitting. A new heuristic for choosing the fresh variables allows to ameliorate the dependency problem, while our novel splitting heuristic, in combination with several other improvements, speeds up the branch-and-bound procedure. We evaluate our approach on the airborne collision avoidance networks ACAS Xu and demonstrate runtime improvements compared to state-of-the-art tools.

Geometric Path Enumeration for Equivalence Verification of Neural Networks

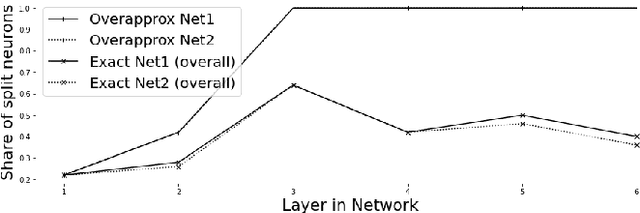
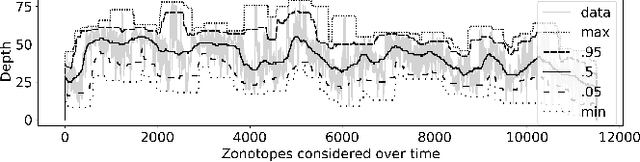
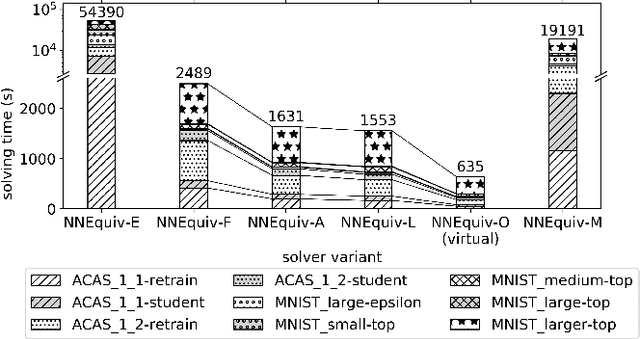
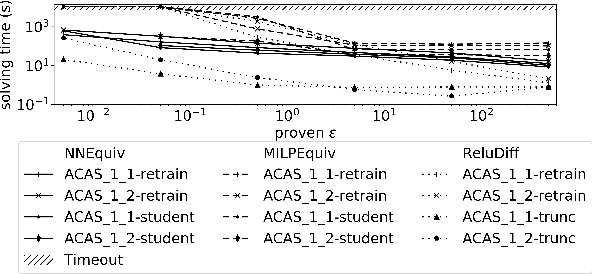
As neural networks (NNs) are increasingly introduced into safety-critical domains, there is a growing need to formally verify NNs before deployment. In this work we focus on the formal verification problem of NN equivalence which aims to prove that two NNs (e.g. an original and a compressed version) show equivalent behavior. Two approaches have been proposed for this problem: Mixed integer linear programming and interval propagation. While the first approach lacks scalability, the latter is only suitable for structurally similar NNs with small weight changes. The contribution of our paper has four parts. First, we show a theoretical result by proving that the epsilon-equivalence problem is coNP-complete. Secondly, we extend Tran et al.'s single NN geometric path enumeration algorithm to a setting with multiple NNs. In a third step, we implement the extended algorithm for equivalence verification and evaluate optimizations necessary for its practical use. Finally, we perform a comparative evaluation showing use-cases where our approach outperforms the previous state of the art, both, for equivalence verification as well as for counter-example finding.