Of Good Demons and Bad Angels: Guaranteeing Safe Control under Finite Precision

As neural networks (NNs) become increasingly prevalent in safety-critical neural network-controlled cyber-physical systems (NNCSs), formally guaranteeing their safety becomes crucial. For these systems, safety must be ensured throughout their entire operation, necessitating infinite-time horizon verification. To verify the infinite-time horizon safety of NNCSs, recent approaches leverage Differential Dynamic Logic (dL). However, these dL-based guarantees rely on idealized, real-valued NN semantics and fail to account for roundoff errors introduced by finite-precision implementations. This paper bridges the gap between theoretical guarantees and real-world implementations by incorporating robustness under finite-precision perturbations -- in sensing, actuation, and computation -- into the safety verification. We model the problem as a hybrid game between a good Demon, responsible for control actions, and a bad Angel, introducing perturbations. This formulation enables formal proofs of robustness w.r.t. a given (bounded) perturbation. Leveraging this bound, we employ state-of-the-art mixed-precision fixed-point tuners to synthesize sound and efficient implementations, thus providing a complete end-to-end solution. We evaluate our approach on case studies from the automotive and aeronautics domains, producing efficient NN implementations with rigorous infinite-time horizon safety guarantees.

Next Steps in LLM-Supported Java Verification

Recent work has shown that Large Language Models (LLMs) are not only a suitable tool for code generation but also capable of generating annotation-based code specifications. Scaling these methodologies may allow us to deduce provable correctness guarantees for large-scale software systems. In comparison to other LLM tasks, the application field of deductive verification has the notable advantage of providing a rigorous toolset to check LLM-generated solutions. This short paper provides early results on how this rigorous toolset can be used to reliably elicit correct specification annotations from an unreliable LLM oracle.

Revisiting Differential Verification: Equivalence Verification with Confidence

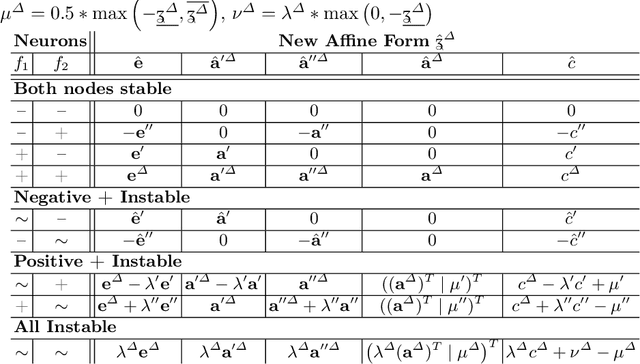
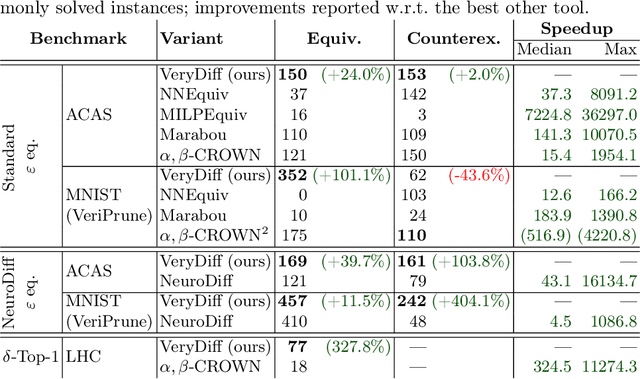
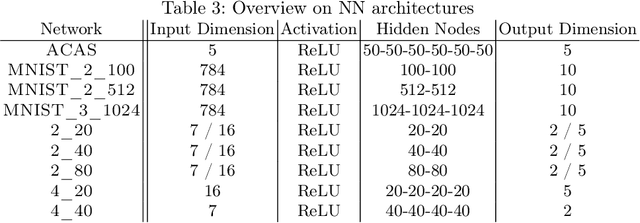
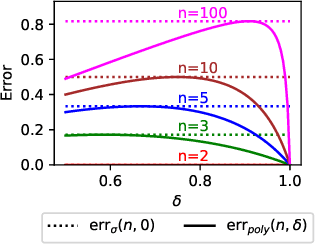
When validated neural networks (NNs) are pruned (and retrained) before deployment, it is desirable to prove that the new NN behaves equivalently to the (original) reference NN. To this end, our paper revisits the idea of differential verification which performs reasoning on differences between NNs: On the one hand, our paper proposes a novel abstract domain for differential verification admitting more efficient reasoning about equivalence. On the other hand, we investigate empirically and theoretically which equivalence properties are (not) efficiently solved using differential reasoning. Based on the gained insights, and following a recent line of work on confidence-based verification, we propose a novel equivalence property that is amenable to Differential Verification while providing guarantees for large parts of the input space instead of small-scale guarantees constructed w.r.t. predetermined input points. We implement our approach in a new tool called VeryDiff and perform an extensive evaluation on numerous old and new benchmark families, including new pruned NNs for particle jet classification in the context of CERN's LHC where we observe median speedups >300x over the State-of-the-Art verifier alpha,beta-CROWN.

An Information-Flow Perspective on Algorithmic Fairness

This work presents insights gained by investigating the relationship between algorithmic fairness and the concept of secure information flow. The problem of enforcing secure information flow is well-studied in the context of information security: If secret information may "flow" through an algorithm or program in such a way that it can influence the program's output, then that is considered insecure information flow as attackers could potentially observe (parts of) the secret. There is a strong correspondence between secure information flow and algorithmic fairness: if protected attributes such as race, gender, or age are treated as secret program inputs, then secure information flow means that these ``secret'' attributes cannot influence the result of a program. While most research in algorithmic fairness evaluation concentrates on studying the impact of algorithms (often treating the algorithm as a black-box), the concepts derived from information flow can be used both for the analysis of disparate treatment as well as disparate impact w.r.t. a structural causal model. In this paper, we examine the relationship between quantitative as well as qualitative information-flow properties and fairness. Moreover, based on this duality, we derive a new quantitative notion of fairness called fairness spread, which can be easily analyzed using quantitative information flow and which strongly relates to counterfactual fairness. We demonstrate that off-the-shelf tools for information-flow properties can be used in order to formally analyze a program's algorithmic fairness properties, including the new notion of fairness spread as well as established notions such as demographic parity.