Verification of Autonomous Neural Car Control with KeYmaera X

This article presents a formal model and formal safety proofs for the ABZ'25 case study in differential dynamic logic (dL). The case study considers an autonomous car driving on a highway avoiding collisions with neighbouring cars. Using KeYmaera X's dL implementation, we prove absence of collision on an infinite time horizon which ensures that safety is preserved independently of trip length. The safety guarantees hold for time-varying reaction time and brake force. Our dL model considers the single lane scenario with cars ahead or behind. We demonstrate that dL with its tools is a rigorous foundation for runtime monitoring, shielding, and neural network verification. Doing so sheds light on inconsistencies between the provided specification and simulation environment highway-env of the ABZ'25 study. We attempt to fix these inconsistencies and uncover numerous counterexamples which also indicate issues in the provided reinforcement learning environment.

Oracular Programming: A Modular Foundation for Building LLM-Enabled Software

Large Language Models have proved surprisingly effective at solving a wide range of tasks from just a handful of examples. However, their lack of reliability and modularity limits their capacity to tackle large problems that require many steps of reasoning. In response, researchers have proposed advanced pipelines that leverage domain-specific knowledge to chain smaller prompts, provide intermediate feedback and improve performance through search. However, the current complexity of writing, tuning, maintaining and improving such pipelines has limited their sophistication. We propose oracular programming, a foundational paradigm for building LLM-enabled applications that lets domain experts express high-level problem-solving strategies as programs with unresolved choice points. These choice points are resolved at runtime by LLMs, which generalize from user-provided examples of correct and incorrect decisions. An oracular program is composed of three orthogonal components: a strategy that consists in a nondeterministic program with choice points that can be reified into a search tree, a policy that specifies how to navigate this tree with the help of LLM oracles, and a set of demonstrations that describe successful and unsuccessful search tree navigation scenarios across diverse problem instances. Each component is expressed in a dedicated programming language and can be independently improved or substituted. We address the key programming language design challenges of modularly composing oracular programs and enforcing consistency between their components as they evolve.

Intersymbolic AI: Interlinking Symbolic AI and Subsymbolic AI

This perspective piece calls for the study of the new field of Intersymbolic AI, by which we mean the combination of symbolic AI, whose building blocks have inherent significance/meaning, with subsymbolic AI, whose entirety creates significance/effect despite the fact that individual building blocks escape meaning. Canonical kinds of symbolic AI are logic, games and planning. Canonical kinds of subsymbolic AI are (un)supervised machine and reinforcement learning. Intersymbolic AI interlinks the worlds of symbolic AI with its compositional symbolic significance and meaning and of subsymbolic AI with its summative significance or effect to enable culminations of insights from both worlds by going between and across symbolic AI insights with subsymbolic AI techniques that are being helped by symbolic AI principles. For example, Intersymbolic AI may start with symbolic AI to understand a dynamic system, continue with subsymbolic AI to learn its control, and end with symbolic AI to safely use the outcome of the learned subsymbolic AI controller in the dynamic system. Intersymbolic AI combines both symbolic and subsymbolic AI to increase the effectiveness of AI compared to either kind of AI alone, in much the same way that the combination of both conscious and subconscious thought increases the effectiveness of human thought compared to either kind of thought alone. Some successful contributions to the Intersymbolic AI paradigm are surveyed here but many more are considered possible by advancing Intersymbolic AI.

Provably Safe Neural Network Controllers via Differential Dynamic Logic

While neural networks (NNs) have a large potential as goal-oriented controllers for Cyber-Physical Systems, verifying the safety of neural network based control systems (NNCSs) poses significant challenges for the practical use of NNs -- especially when safety is needed for unbounded time horizons. One reason for this is the intractability of NN and hybrid system analysis. We introduce VerSAILLE (Verifiably Safe AI via Logically Linked Envelopes): The first approach for the combination of differential dynamic logic (dL) and NN verification. By joining forces, we can exploit the efficiency of NN verification tools while retaining the rigor of dL. We reflect a safety proof for a controller envelope in an NN to prove the safety of concrete NNCS on an infinite-time horizon. The NN verification properties resulting from VerSAILLE typically require nonlinear arithmetic while efficient NN verification tools merely support linear arithmetic. To overcome this divide, we present Mosaic: The first sound and complete verification approach for polynomial real arithmetic properties on piece-wise linear NNs. Mosaic lifts off-the-shelf tools for linear properties to the nonlinear setting. An evaluation on case studies, including adaptive cruise control and airborne collision avoidance, demonstrates the versatility of VerSAILLE and Mosaic: It supports the certification of infinite-time horizon safety and the exhaustive enumeration of counterexample regions while significantly outperforming State-of-the-Art tools in closed-loop NNV.

Learning to Find Proofs and Theorems by Learning to Refine Search Strategies

We propose a new approach to automated theorem proving and deductive program synthesis where an AlphaZero-style agent is self-training to refine a high-level expert strategy expressed as a nondeterministic program. An analogous teacher agent is self-training to generate tasks of suitable relevance and difficulty for the learner. This allows leveraging minimal amounts of domain knowledge to tackle problems for which training data is unavailable or hard to synthesize. We illustrate our approach on the problem of loop invariant synthesis for imperative programs and using neural networks to refine both the teacher and solver strategies.

Blackbox End-to-End Verification of Ground Robot Safety and Liveness

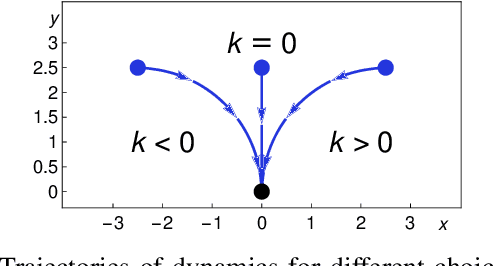
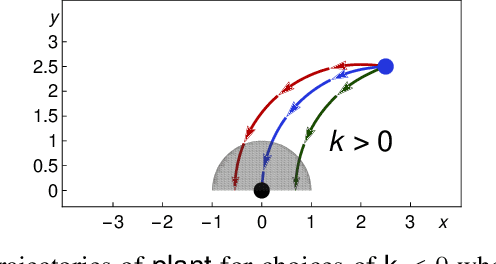
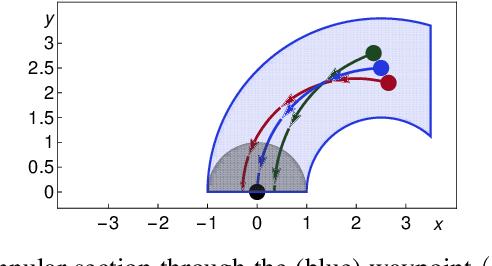
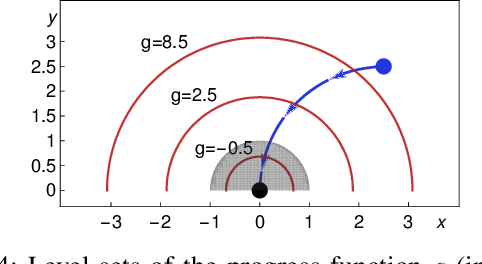
We formally prove end-to-end correctness of a ground robot implemented in a simulator. We use an untrusted controller supervised by a verified sandbox. Contributions include: (i) A model of the robot in differential dynamic logic, which specifies assumptions on the controller and robot kinematics, (ii) Formal proofs of safety and liveness for a waypoint-following problem with speed limits, (iii) An automatically synthesized sandbox, which is automatically proven to enforce model compliance at runtime, and (iv) Controllers, planners, and environments for the simulations. The verified sandbox is used to safeguard (unverified) controllers in a realistic simulated environment. Experimental evaluation of the resulting sandboxed implementation confirms safety and high model-compliance, with an inherent trade-off between compliance and performance. The verified sandbox thus serves as a valuable bidirectional link between formal methods and implementation, automating both enforcement of safety and model validation simultaneously.

Formal Verification of Obstacle Avoidance and Navigation of Ground Robots

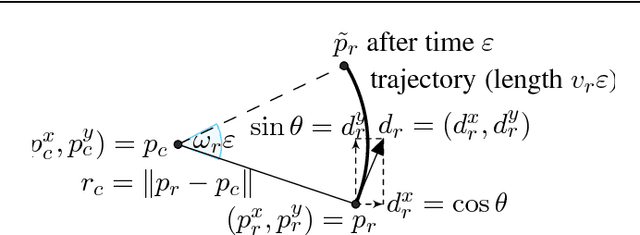
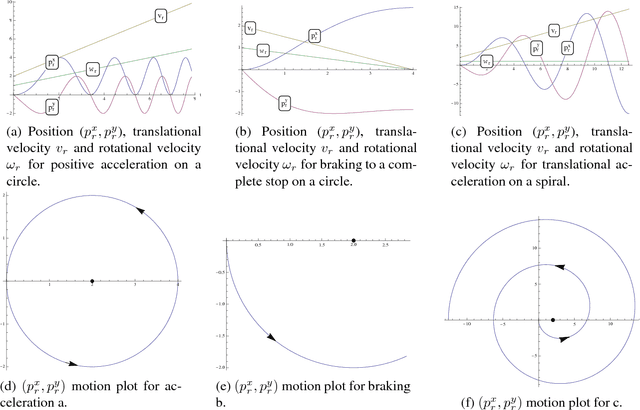
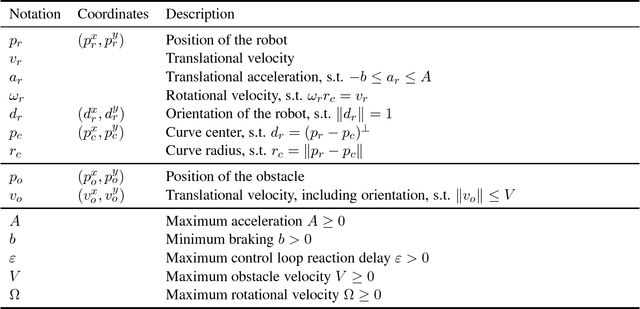
The safety of mobile robots in dynamic environments is predicated on making sure that they do not collide with obstacles. In support of such safety arguments, we analyze and formally verify a series of increasingly powerful safety properties of controllers for avoiding both stationary and moving obstacles: (i) static safety, which ensures that no collisions can happen with stationary obstacles, (ii) passive safety, which ensures that no collisions can happen with stationary or moving obstacles while the robot moves, (iii) the stronger passive friendly safety in which the robot further maintains sufficient maneuvering distance for obstacles to avoid collision as well, and (iv) passive orientation safety, which allows for imperfect sensor coverage of the robot, i. e., the robot is aware that not everything in its environment will be visible. We complement these provably correct safety properties with liveness properties: we prove that provably safe motion is flexible enough to let the robot still navigate waypoints and pass intersections. We use hybrid system models and theorem proving techniques that describe and formally verify the robot's discrete control decisions along with its continuous, physical motion. Moreover, we formally prove that safety can still be guaranteed despite sensor uncertainty and actuator perturbation, and when control choices for more aggressive maneuvers are introduced. Our verification results are generic in the sense that they are not limited to the particular choices of one specific control algorithm but identify conditions that make them simultaneously apply to a broad class of control algorithms.