Fixing That Free Lunch: When, Where, and Why Synthetic Data Fails in Model-Based Policy Optimization

Synthetic data is a core component of data-efficient Dyna-style model-based reinforcement learning, yet it can also degrade performance. We study when it helps, where it fails, and why, and we show that addressing the resulting failure modes enables policy improvement that was previously unattainable. We focus on Model-Based Policy Optimization (MBPO), which performs actor and critic updates using synthetic action counterfactuals. Despite reports of strong and generalizable sample-efficiency gains in OpenAI Gym, recent work shows that MBPO often underperforms its model-free counterpart, Soft Actor-Critic (SAC), in the DeepMind Control Suite (DMC). Although both suites involve continuous control with proprioceptive robots, this shift leads to sharp performance losses across seven challenging DMC tasks, with MBPO failing in cases where claims of generalization from Gym would imply success. This reveals how environment-specific assumptions can become implicitly encoded into algorithm design when evaluation is limited. We identify two coupled issues behind these failures: scale mismatches between dynamics and reward models that induce critic underestimation and hinder policy improvement during model-policy coevolution, and a poor choice of target representation that inflates model variance and produces error-prone rollouts. Addressing these failure modes enables policy improvement where none was previously possible, allowing MBPO to outperform SAC in five of seven tasks while preserving the strong performance previously reported in OpenAI Gym. Rather than aiming only for incremental average gains, we hope our findings motivate the community to develop taxonomies that tie MDP task- and environment-level structure to algorithmic failure modes, pursue unified solutions where possible, and clarify how benchmark choices ultimately shape the conditions under which algorithms generalize.

SCOPED: Score-Curvature Out-of-distribution Proximity Evaluator for Diffusion

Out-of-distribution (OOD) detection is essential for reliable deployment of machine learning systems in vision, robotics, reinforcement learning, and beyond. We introduce Score-Curvature Out-of-distribution Proximity Evaluator for Diffusion (SCOPED), a fast and general-purpose OOD detection method for diffusion models that reduces the number of forward passes on the trained model by an order of magnitude compared to prior methods, outperforming most diffusion-based baselines and closely approaching the accuracy of the strongest ones. SCOPED is computed from a single diffusion model trained once on a diverse dataset, and combines the Jacobian trace and squared norm of the model's score function into a single test statistic. Rather than thresholding on a fixed value, we estimate the in-distribution density of SCOPED scores using kernel density estimation, enabling a flexible, unsupervised test that, in the simplest case, only requires a single forward pass and one Jacobian-vector product (JVP), made efficient by Hutchinson's trace estimator. On four vision benchmarks, SCOPED achieves competitive or state-of-the-art precision-recall scores despite its low computational cost. The same method generalizes to robotic control tasks with shared state and action spaces, identifying distribution shifts across reward functions and training regimes. These results position SCOPED as a practical foundation for fast and reliable OOD detection in real-world domains, including perceptual artifacts in vision, outlier detection in autoregressive models, exploration in reinforcement learning, and dataset curation for unsupervised training.

SHIELD: Safety on Humanoids via CBFs In Expectation on Learned Dynamics

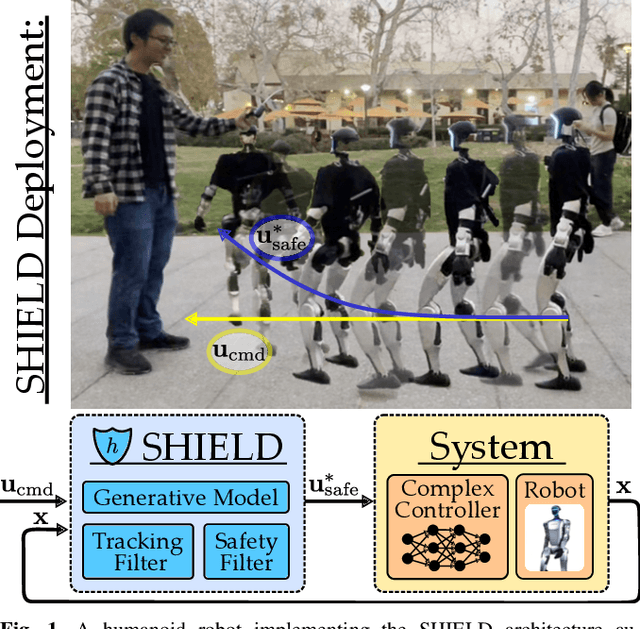
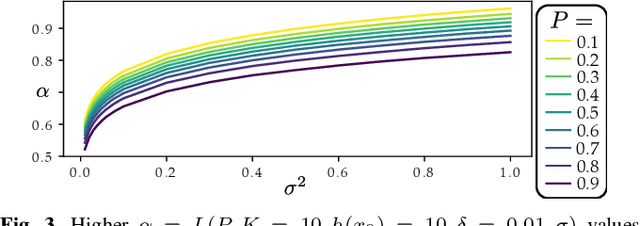
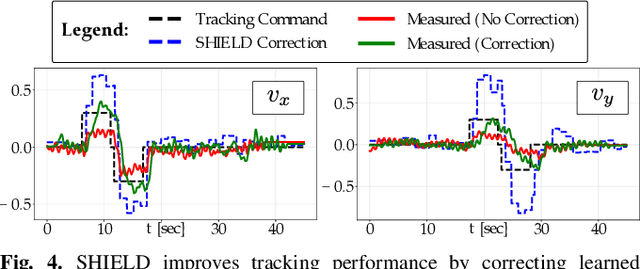
Robot learning has produced remarkably effective ``black-box'' controllers for complex tasks such as dynamic locomotion on humanoids. Yet ensuring dynamic safety, i.e., constraint satisfaction, remains challenging for such policies. Reinforcement learning (RL) embeds constraints heuristically through reward engineering, and adding or modifying constraints requires retraining. Model-based approaches, like control barrier functions (CBFs), enable runtime constraint specification with formal guarantees but require accurate dynamics models. This paper presents SHIELD, a layered safety framework that bridges this gap by: (1) training a generative, stochastic dynamics residual model using real-world data from hardware rollouts of the nominal controller, capturing system behavior and uncertainties; and (2) adding a safety layer on top of the nominal (learned locomotion) controller that leverages this model via a stochastic discrete-time CBF formulation enforcing safety constraints in probability. The result is a minimally-invasive safety layer that can be added to the existing autonomy stack to give probabilistic guarantees of safety that balance risk and performance. In hardware experiments on an Unitree G1 humanoid, SHIELD enables safe navigation (obstacle avoidance) through varied indoor and outdoor environments using a nominal (unknown) RL controller and onboard perception.

Real-Time Privacy Preservation for Robot Visual Perception

Many robots (e.g., iRobot's Roomba) operate based on visual observations from live video streams, and such observations may inadvertently include privacy-sensitive objects, such as personal identifiers. Existing approaches for preserving privacy rely on deep learning models, differential privacy, or cryptography. They lack guarantees for the complete concealment of all sensitive objects. Guaranteeing concealment requires post-processing techniques and thus is inadequate for real-time video streams. We develop a method for privacy-constrained video streaming, PCVS, that conceals sensitive objects within real-time video streams. PCVS takes a logical specification constraining the existence of privacy-sensitive objects, e.g., never show faces when a person exists. It uses a detection model to evaluate the existence of these objects in each incoming frame. Then, it blurs out a subset of objects such that the existence of the remaining objects satisfies the specification. We then propose a conformal prediction approach to (i) establish a theoretical lower bound on the probability of the existence of these objects in a sequence of frames satisfying the specification and (ii) update the bound with the arrival of each subsequent frame. Quantitative evaluations show that PCVS achieves over 95 percent specification satisfaction rate in multiple datasets, significantly outperforming other methods. The satisfaction rate is consistently above the theoretical bounds across all datasets, indicating that the established bounds hold. Additionally, we deploy PCVS on robots in real-time operation and show that the robots operate normally without being compromised when PCVS conceals objects.

Act Natural! Extending Naturalistic Projection to Multimodal Behavior Scenarios

Autonomous agents operating in public spaces must consider how their behaviors might affect the humans around them, even when not directly interacting with them. To this end, it is often beneficial to be predictable and appear naturalistic. Existing methods for this purpose use human actor intent modeling or imitation learning techniques, but these approaches rarely capture all possible motivations for human behavior and/or require significant amounts of data. Our work extends a technique for modeling unimodal naturalistic behaviors with an explicit convex set representation, to account for multimodal behavior by using multiple convex sets. This more flexible representation provides a higher degree of fidelity in data-driven modeling of naturalistic behavior that arises in real-world scenarios in which human behavior is, in some sense, discrete, e.g. whether or not to yield at a roundabout. Equipped with this new set representation, we develop an optimization-based filter to project arbitrary trajectories into the set so that they appear naturalistic to humans in the scene, while also satisfying vehicle dynamics, actuator limits, etc. We demonstrate our methods on real-world human driving data from the inD (intersection) and rounD (roundabout) datasets.

PSN Game: Game-theoretic Planning via a Player Selection Network

While game-theoretic planning frameworks are effective at modeling multi-agent interactions, they require solving optimization problems with hundreds or thousands of variables, resulting in long computation times that limit their use in large-scale, real-time systems. To address this issue, we propose PSN Game: a novel game-theoretic planning framework that reduces runtime by learning a Player Selection Network (PSN). A PSN outputs a player selection mask that distinguishes influential players from less relevant ones, enabling the ego player to solve a smaller, masked game involving only selected players. By reducing the number of variables in the optimization problem, PSN directly lowers computation time. The PSN Game framework is more flexible than existing player selection methods as it i) relies solely on observations of players' past trajectories, without requiring full state, control, or other game-specific information; and ii) requires no online parameter tuning. We train PSNs in an unsupervised manner using a differentiable dynamic game solver, with reference trajectories from full-player games guiding the learning. Experiments in both simulated scenarios and human trajectory datasets demonstrate that i) PSNs outperform baseline selection methods in trajectory smoothness and length, while maintaining comparable safety and achieving a 10x speedup in runtime; and ii) PSNs generalize effectively to real-world scenarios without fine-tuning. By selecting only the most relevant players for decision-making, PSNs offer a general mechanism for reducing planning complexity that can be seamlessly integrated into existing multi-agent planning frameworks.

Meta-Learning Online Dynamics Model Adaptation in Off-Road Autonomous Driving

High-speed off-road autonomous driving presents unique challenges due to complex, evolving terrain characteristics and the difficulty of accurately modeling terrain-vehicle interactions. While dynamics models used in model-based control can be learned from real-world data, they often struggle to generalize to unseen terrain, making real-time adaptation essential. We propose a novel framework that combines a Kalman filter-based online adaptation scheme with meta-learned parameters to address these challenges. Offline meta-learning optimizes the basis functions along which adaptation occurs, as well as the adaptation parameters, while online adaptation dynamically adjusts the onboard dynamics model in real time for model-based control. We validate our approach through extensive experiments, including real-world testing on a full-scale autonomous off-road vehicle, demonstrating that our method outperforms baseline approaches in prediction accuracy, performance, and safety metrics, particularly in safety-critical scenarios. Our results underscore the effectiveness of meta-learned dynamics model adaptation, advancing the development of reliable autonomous systems capable of navigating diverse and unseen environments. Video is available at: https://youtu.be/cCKHHrDRQEA

Multi-Fidelity Policy Gradient Algorithms

Many reinforcement learning (RL) algorithms require large amounts of data, prohibiting their use in applications where frequent interactions with operational systems are infeasible, or high-fidelity simulations are expensive or unavailable. Meanwhile, low-fidelity simulators--such as reduced-order models, heuristic reward functions, or generative world models--can cheaply provide useful data for RL training, even if they are too coarse for direct sim-to-real transfer. We propose multi-fidelity policy gradients (MFPGs), an RL framework that mixes a small amount of data from the target environment with a large volume of low-fidelity simulation data to form unbiased, reduced-variance estimators (control variates) for on-policy policy gradients. We instantiate the framework by developing multi-fidelity variants of two policy gradient algorithms: REINFORCE and proximal policy optimization. Experimental results across a suite of simulated robotics benchmark problems demonstrate that when target-environment samples are limited, MFPG achieves up to 3.9x higher reward and improves training stability when compared to baselines that only use high-fidelity data. Moreover, even when the baselines are given more high-fidelity samples--up to 10x as many interactions with the target environment--MFPG continues to match or outperform them. Finally, we observe that MFPG is capable of training effective policies even when the low-fidelity environment is drastically different from the target environment. MFPG thus not only offers a novel paradigm for efficient sim-to-real transfer but also provides a principled approach to managing the trade-off between policy performance and data collection costs.

Stealing That Free Lunch: Exposing the Limits of Dyna-Style Reinforcement Learning

Dyna-style off-policy model-based reinforcement learning (DMBRL) algorithms are a family of techniques for generating synthetic state transition data and thereby enhancing the sample efficiency of off-policy RL algorithms. This paper identifies and investigates a surprising performance gap observed when applying DMBRL algorithms across different benchmark environments with proprioceptive observations. We show that, while DMBRL algorithms perform well in OpenAI Gym, their performance can drop significantly in DeepMind Control Suite (DMC), even though these settings offer similar tasks and identical physics backends. Modern techniques designed to address several key issues that arise in these settings do not provide a consistent improvement across all environments, and overall our results show that adding synthetic rollouts to the training process -- the backbone of Dyna-style algorithms -- significantly degrades performance across most DMC environments. Our findings contribute to a deeper understanding of several fundamental challenges in model-based RL and show that, like many optimization fields, there is no free lunch when evaluating performance across diverse benchmarks in RL.

Dense Dynamics-Aware Reward Synthesis: Integrating Prior Experience with Demonstrations

Many continuous control problems can be formulated as sparse-reward reinforcement learning (RL) tasks. In principle, online RL methods can automatically explore the state space to solve each new task. However, discovering sequences of actions that lead to a non-zero reward becomes exponentially more difficult as the task horizon increases. Manually shaping rewards can accelerate learning for a fixed task, but it is an arduous process that must be repeated for each new environment. We introduce a systematic reward-shaping framework that distills the information contained in 1) a task-agnostic prior data set and 2) a small number of task-specific expert demonstrations, and then uses these priors to synthesize dense dynamics-aware rewards for the given task. This supervision substantially accelerates learning in our experiments, and we provide analysis demonstrating how the approach can effectively guide online learning agents to faraway goals.