Inferring Short-Sightedness in Dynamic Noncooperative Games
Paper and Code
Dec 02, 2024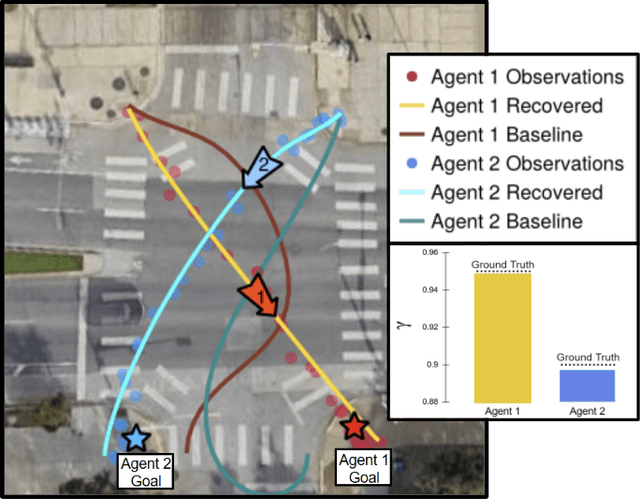
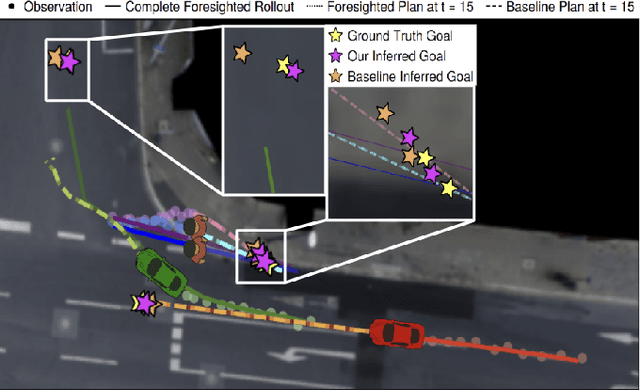
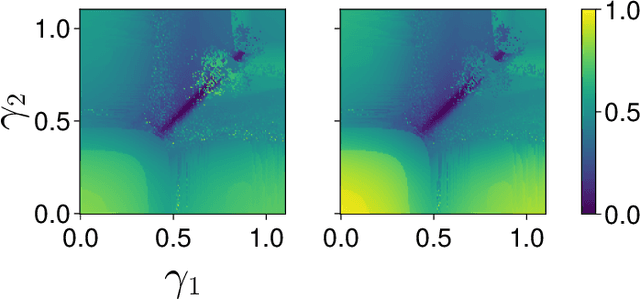
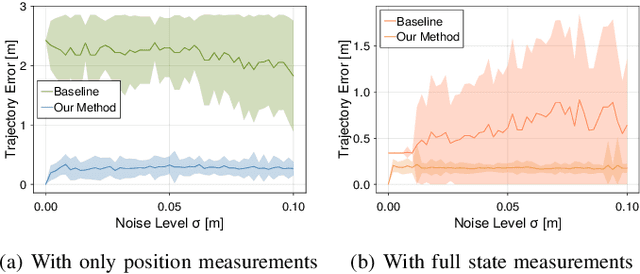
Dynamic game theory is an increasingly popular tool for modeling multi-agent, e.g. human-robot, interactions. Game-theoretic models presume that each agent wishes to minimize a private cost function that depends on others' actions. These games typically evolve over a fixed time horizon, which specifies the degree to which all agents care about the distant future. In practical settings, however, decision-makers may vary in their degree of short-sightedness. We conjecture that quantifying and estimating each agent's short-sightedness from online data will enable safer and more efficient interactions with other agents. To this end, we frame this inference problem as an inverse dynamic game. We consider a specific parametrization of each agent's objective function that smoothly interpolates myopic and farsighted planning. Games of this form are readily transformed into parametric mixed complementarity problems; we exploit the directional differentiability of solutions to these problems with respect to their hidden parameters in order to solve for agents' short-sightedness. We conduct several experiments simulating human behavior at a real-world crosswalk. The results of these experiments clearly demonstrate that by explicitly inferring agents' short-sightedness, we can recover more accurate game-theoretic models, which ultimately allow us to make better predictions of agents' behavior. Specifically, our results show up to a 30% more accurate prediction of myopic behavior compared to the baseline.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge