Multi-Fidelity Policy Gradient Algorithms

Many reinforcement learning (RL) algorithms require large amounts of data, prohibiting their use in applications where frequent interactions with operational systems are infeasible, or high-fidelity simulations are expensive or unavailable. Meanwhile, low-fidelity simulators--such as reduced-order models, heuristic reward functions, or generative world models--can cheaply provide useful data for RL training, even if they are too coarse for direct sim-to-real transfer. We propose multi-fidelity policy gradients (MFPGs), an RL framework that mixes a small amount of data from the target environment with a large volume of low-fidelity simulation data to form unbiased, reduced-variance estimators (control variates) for on-policy policy gradients. We instantiate the framework by developing multi-fidelity variants of two policy gradient algorithms: REINFORCE and proximal policy optimization. Experimental results across a suite of simulated robotics benchmark problems demonstrate that when target-environment samples are limited, MFPG achieves up to 3.9x higher reward and improves training stability when compared to baselines that only use high-fidelity data. Moreover, even when the baselines are given more high-fidelity samples--up to 10x as many interactions with the target environment--MFPG continues to match or outperform them. Finally, we observe that MFPG is capable of training effective policies even when the low-fidelity environment is drastically different from the target environment. MFPG thus not only offers a novel paradigm for efficient sim-to-real transfer but also provides a principled approach to managing the trade-off between policy performance and data collection costs.

Inferring Short-Sightedness in Dynamic Noncooperative Games

Dynamic game theory is an increasingly popular tool for modeling multi-agent, e.g. human-robot, interactions. Game-theoretic models presume that each agent wishes to minimize a private cost function that depends on others' actions. These games typically evolve over a fixed time horizon, which specifies the degree to which all agents care about the distant future. In practical settings, however, decision-makers may vary in their degree of short-sightedness. We conjecture that quantifying and estimating each agent's short-sightedness from online data will enable safer and more efficient interactions with other agents. To this end, we frame this inference problem as an inverse dynamic game. We consider a specific parametrization of each agent's objective function that smoothly interpolates myopic and farsighted planning. Games of this form are readily transformed into parametric mixed complementarity problems; we exploit the directional differentiability of solutions to these problems with respect to their hidden parameters in order to solve for agents' short-sightedness. We conduct several experiments simulating human behavior at a real-world crosswalk. The results of these experiments clearly demonstrate that by explicitly inferring agents' short-sightedness, we can recover more accurate game-theoretic models, which ultimately allow us to make better predictions of agents' behavior. Specifically, our results show up to a 30% more accurate prediction of myopic behavior compared to the baseline.

Policies with Sparse Inter-Agent Dependencies in Dynamic Games: A Dynamic Programming Approach

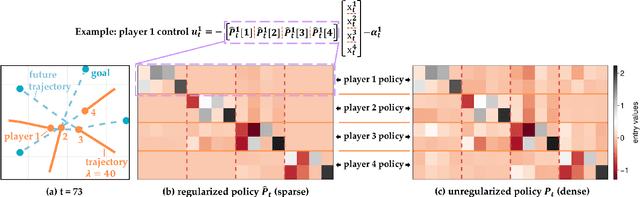
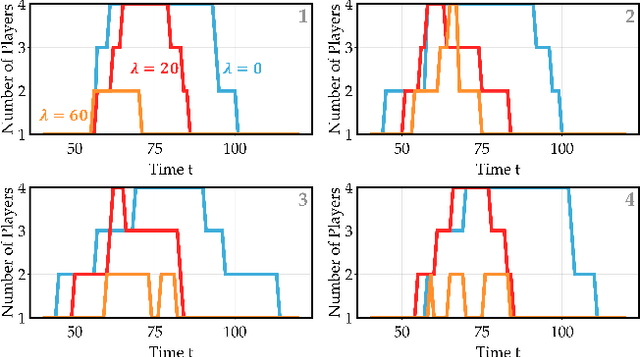
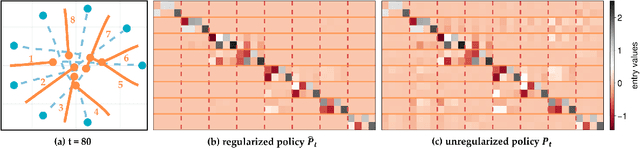
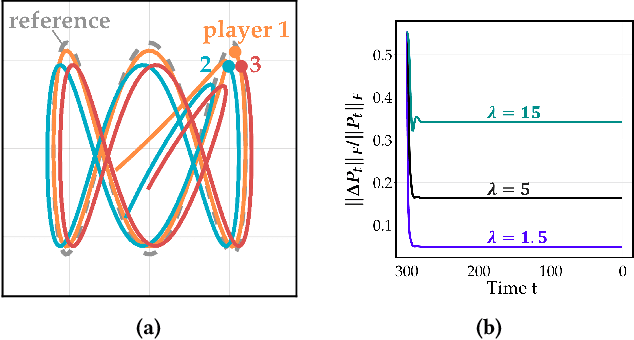
Common feedback strategies in multi-agent dynamic games require all players' state information to compute control strategies. However, in real-world scenarios, sensing and communication limitations between agents make full state feedback expensive or impractical, and such strategies can become fragile when state information from other agents is inaccurate. To this end, we propose a regularized dynamic programming approach for finding sparse feedback policies that selectively depend on the states of a subset of agents in dynamic games. The proposed approach solves convex adaptive group Lasso problems to compute sparse policies approximating Nash equilibrium solutions. We prove the regularized solutions' asymptotic convergence to a neighborhood of Nash equilibrium policies in linear-quadratic (LQ) games. We extend the proposed approach to general non-LQ games via an iterative algorithm. Empirical results in multi-robot interaction scenarios show that the proposed approach effectively computes feedback policies with varying sparsity levels. When agents have noisy observations of other agents' states, simulation results indicate that the proposed regularized policies consistently achieve lower costs than standard Nash equilibrium policies by up to 77% for all interacting agents whose costs are coupled with other agents' states.

Auto-Encoding Bayesian Inverse Games

When multiple agents interact in a common environment, each agent's actions impact others' future decisions, and noncooperative dynamic games naturally capture this coupling. In interactive motion planning, however, agents typically do not have access to a complete model of the game, e.g., due to unknown objectives of other players. Therefore, we consider the inverse game problem, in which some properties of the game are unknown a priori and must be inferred from observations. Existing maximum likelihood estimation (MLE) approaches to solve inverse games provide only point estimates of unknown parameters without quantifying uncertainty, and perform poorly when many parameter values explain the observed behavior. To address these limitations, we take a Bayesian perspective and construct posterior distributions of game parameters. To render inference tractable, we employ a variational autoencoder (VAE) with an embedded differentiable game solver. This structured VAE can be trained from an unlabeled dataset of observed interactions, naturally handles continuous, multi-modal distributions, and supports efficient sampling from the inferred posteriors without computing game solutions at runtime. Extensive evaluations in simulated driving scenarios demonstrate that the proposed approach successfully learns the prior and posterior objective distributions, provides more accurate objective estimates than MLE baselines, and facilitates safer and more efficient game-theoretic motion planning.

Learning to Play Trajectory Games Against Opponents with Unknown Objectives

Many autonomous agents, such as intelligent vehicles, are inherently required to interact with one another. Game theory provides a natural mathematical tool for robot motion planning in such interactive settings. However, tractable algorithms for such problems usually rely on a strong assumption, namely that the objectives of all players in the scene are known. To make such tools applicable for ego-centric planning with only local information, we propose an adaptive model-predictive game solver, which jointly infers other players' objectives online and computes a corresponding generalized Nash equilibrium (GNE) strategy. The adaptivity of our approach is enabled by a differentiable trajectory game solver whose gradient signal is used for maximum likelihood estimation (MLE) of opponents' objectives. This differentiability of our pipeline facilitates direct integration with other differentiable elements, such as neural networks (NNs). Furthermore, in contrast to existing solvers for cost inference in games, our method handles not only partial state observations but also general inequality constraints. In two simulated traffic scenarios, we find superior performance of our approach over both existing game-theoretic methods and non-game-theoretic model-predictive control (MPC) approaches. We also demonstrate our approach's real-time planning capabilities and robustness in two hardware experiments.

Safe Model Predictive Control Approach for Non-holonomic Mobile Robots

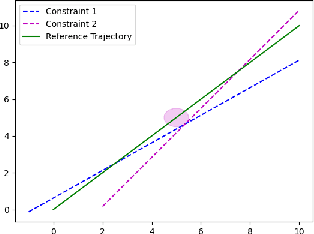
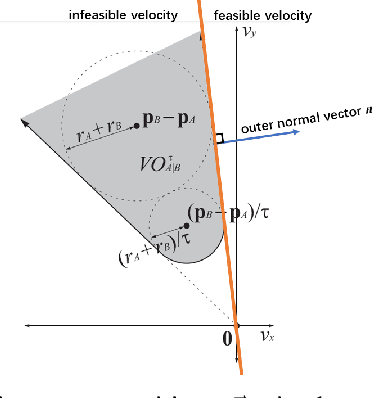
We design an MPC approach for non-holonomic mobile robots and analytically show that the time-varying, linearized system can yield asymptotic stability around the origin in the tracking task. For obstacle avoidance, we propose a constraint in velocity-space which explicitly couples the two control inputs based on the current state.