Lasse Peters
Bayesian Inverse Games with High-Dimensional Multi-Modal Observations
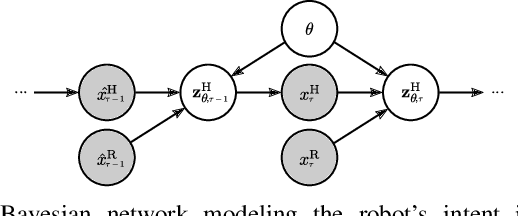
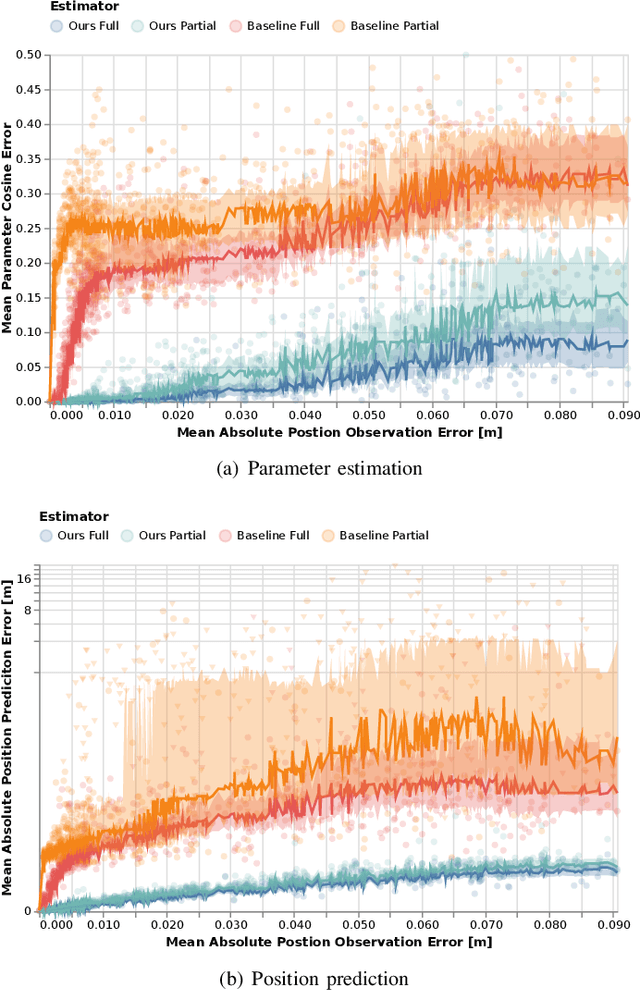
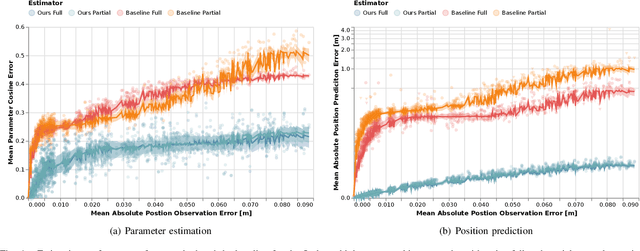
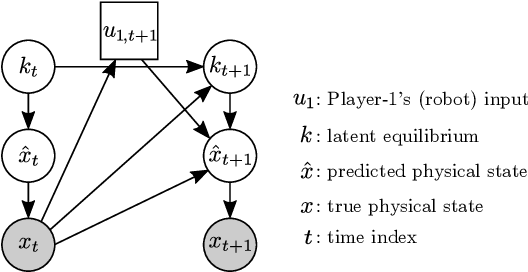
Jan 02, 2026Abstract:Many multi-agent interaction scenarios can be naturally modeled as noncooperative games, where each agent's decisions depend on others' future actions. However, deploying game-theoretic planners for autonomous decision-making requires a specification of all agents' objectives. To circumvent this practical difficulty, recent work develops maximum likelihood techniques for solving inverse games that can identify unknown agent objectives from interaction data. Unfortunately, these methods only infer point estimates and do not quantify estimator uncertainty; correspondingly, downstream planning decisions can overconfidently commit to unsafe actions. We present an approximate Bayesian inference approach for solving the inverse game problem, which can incorporate observation data from multiple modalities and be used to generate samples from the Bayesian posterior over the hidden agent objectives given limited sensor observations in real time. Concretely, the proposed Bayesian inverse game framework trains a structured variational autoencoder with an embedded differentiable Nash game solver on interaction datasets and does not require labels of agents' true objectives. Extensive experiments show that our framework successfully learns prior and posterior distributions, improves inference quality over maximum likelihood estimation-based inverse game approaches, and enables safer downstream decision-making without sacrificing efficiency. When trajectory information is uninformative or unavailable, multimodal inference further reduces uncertainty by exploiting additional observation modalities.
Generalizing Safety Beyond Collision-Avoidance via Latent-Space Reachability Analysis
Feb 02, 2025Abstract:Hamilton-Jacobi (HJ) reachability is a rigorous mathematical framework that enables robots to simultaneously detect unsafe states and generate actions that prevent future failures. While in theory, HJ reachability can synthesize safe controllers for nonlinear systems and nonconvex constraints, in practice, it has been limited to hand-engineered collision-avoidance constraints modeled via low-dimensional state-space representations and first-principles dynamics. In this work, our goal is to generalize safe robot controllers to prevent failures that are hard -- if not impossible -- to write down by hand, but can be intuitively identified from high-dimensional observations: for example, spilling the contents of a bag. We propose Latent Safety Filters, a latent-space generalization of HJ reachability that tractably operates directly on raw observation data (e.g., RGB images) by performing safety analysis in the latent embedding space of a generative world model. This transforms nuanced constraint specification to a classification problem in latent space and enables reasoning about dynamical consequences that are hard to simulate. In simulation and hardware experiments, we use Latent Safety Filters to safeguard arbitrary policies (from generative policies to direct teleoperation) from complex safety hazards, like preventing a Franka Research 3 manipulator from spilling the contents of a bag or toppling cluttered objects.
Updating Robot Safety Representations Online from Natural Language Feedback
Sep 22, 2024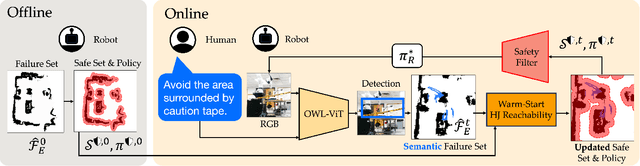
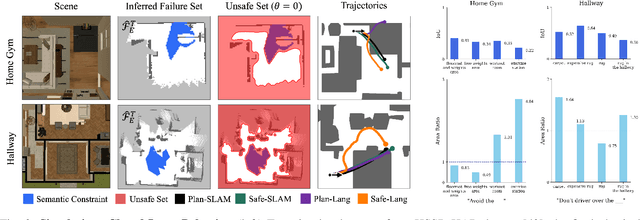
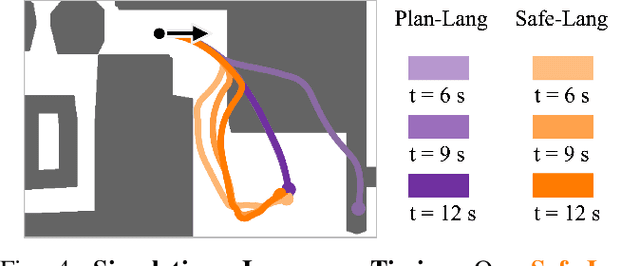
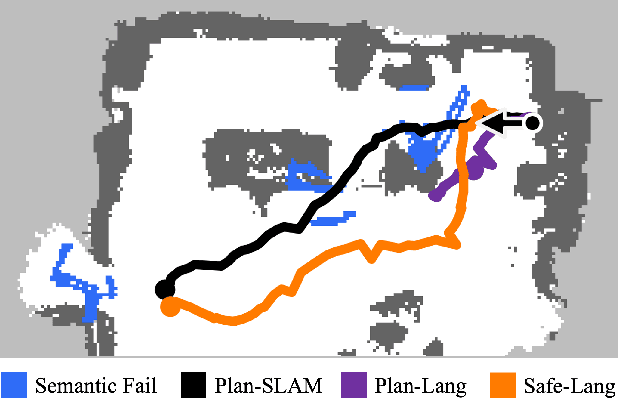
Abstract:Robots must operate safely when deployed in novel and human-centered environments, like homes. Current safe control approaches typically assume that the safety constraints are known a priori, and thus, the robot can pre-compute a corresponding safety controller. While this may make sense for some safety constraints (e.g., avoiding collision with walls by analyzing a floor plan), other constraints are more complex (e.g., spills), inherently personal, context-dependent, and can only be identified at deployment time when the robot is interacting in a specific environment and with a specific person (e.g., fragile objects, expensive rugs). Here, language provides a flexible mechanism to communicate these evolving safety constraints to the robot. In this work, we use vision language models (VLMs) to interpret language feedback and the robot's image observations to continuously update the robot's representation of safety constraints. With these inferred constraints, we update a Hamilton-Jacobi reachability safety controller online via efficient warm-starting techniques. Through simulation and hardware experiments, we demonstrate the robot's ability to infer and respect language-based safety constraints with the proposed approach.
Auto-Encoding Bayesian Inverse Games
Feb 16, 2024Abstract:When multiple agents interact in a common environment, each agent's actions impact others' future decisions, and noncooperative dynamic games naturally capture this coupling. In interactive motion planning, however, agents typically do not have access to a complete model of the game, e.g., due to unknown objectives of other players. Therefore, we consider the inverse game problem, in which some properties of the game are unknown a priori and must be inferred from observations. Existing maximum likelihood estimation (MLE) approaches to solve inverse games provide only point estimates of unknown parameters without quantifying uncertainty, and perform poorly when many parameter values explain the observed behavior. To address these limitations, we take a Bayesian perspective and construct posterior distributions of game parameters. To render inference tractable, we employ a variational autoencoder (VAE) with an embedded differentiable game solver. This structured VAE can be trained from an unlabeled dataset of observed interactions, naturally handles continuous, multi-modal distributions, and supports efficient sampling from the inferred posteriors without computing game solutions at runtime. Extensive evaluations in simulated driving scenarios demonstrate that the proposed approach successfully learns the prior and posterior objective distributions, provides more accurate objective estimates than MLE baselines, and facilitates safer and more efficient game-theoretic motion planning.
Contingency Games for Multi-Agent Interaction
Apr 14, 2023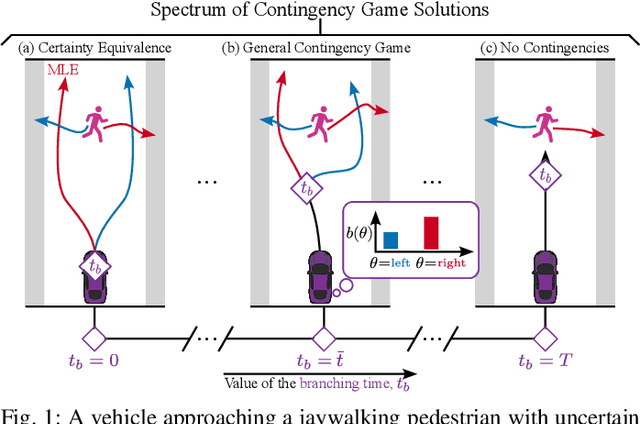
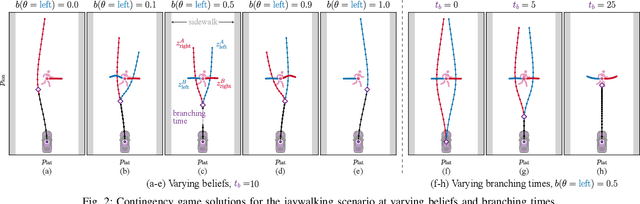
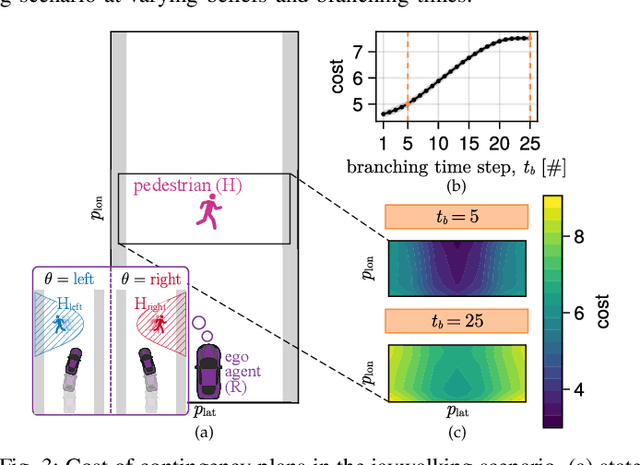
Abstract:Contingency planning, wherein an agent generates a set of possible plans conditioned on the outcome of an uncertain event, is an increasingly popular way for robots to act under uncertainty. In this work, we take a game-theoretic perspective on contingency planning which is tailored to multi-agent scenarios in which a robot's actions impact the decisions of other agents and vice versa. The resulting contingency game allows the robot to efficiently coordinate with other agents by generating strategic motion plans conditioned on multiple possible intents for other actors in the scene. Contingency games are parameterized via a scalar variable which represents a future time at which intent uncertainty will be resolved. Varying this parameter enables a designer to easily adjust how conservatively the robot behaves in the game. Interestingly, we also find that existing variants of game-theoretic planning under uncertainty are readily obtained as special cases of contingency games. Lastly, we offer an efficient method for solving N-player contingency games with nonlinear dynamics and non-convex costs and constraints. Through a series of simulated autonomous driving scenarios, we demonstrate that plans generated via contingency games provide quantitative performance gains over game-theoretic motion plans that do not account for future uncertainty reduction.
Learning Players' Objectives in Continuous Dynamic Games from Partial State Observations
Feb 03, 2023



Abstract:Robots deployed to the real world must be able to interact with other agents in their environment. Dynamic game theory provides a powerful mathematical framework for modeling scenarios in which agents have individual objectives and interactions evolve over time. However, a key limitation of such techniques is that they require a-priori knowledge of all players' objectives. In this work, we address this issue by proposing a novel method for learning players' objectives in continuous dynamic games from noise-corrupted, partial state observations. Our approach learns objectives by coupling the estimation of unknown cost parameters of each player with inference of unobserved states and inputs through Nash equilibrium constraints. By coupling past state estimates with future state predictions, our approach is amenable to simultaneous online learning and prediction in receding horizon fashion. We demonstrate our method in several simulated traffic scenarios in which we recover players' preferences for, e.g., desired travel speed and collision-avoidance behavior. Results show that our method reliably estimates game-theoretic models from noise-corrupted data that closely matches ground-truth objectives, consistently outperforming state-of-the-art approaches.
Cost Inference for Feedback Dynamic Games from Noisy Partial State Observations and Incomplete Trajectories
Jan 04, 2023



Abstract:In multi-agent dynamic games, the Nash equilibrium state trajectory of each agent is determined by its cost function and the information pattern of the game. However, the cost and trajectory of each agent may be unavailable to the other agents. Prior work on using partial observations to infer the costs in dynamic games assumes an open-loop information pattern. In this work, we demonstrate that the feedback Nash equilibrium concept is more expressive and encodes more complex behavior. It is desirable to develop specific tools for inferring players' objectives in feedback games. Therefore, we consider the dynamic game cost inference problem under the feedback information pattern, using only partial state observations and incomplete trajectory data. To this end, we first propose an inverse feedback game loss function, whose minimizer yields a feedback Nash equilibrium state trajectory closest to the observation data. We characterize the landscape and differentiability of the loss function. Given the difficulty of obtaining the exact gradient, our main contribution is an efficient gradient approximator, which enables a novel inverse feedback game solver that minimizes the loss using first-order optimization. In thorough empirical evaluations, we demonstrate that our algorithm converges reliably and has better robustness and generalization performance than the open-loop baseline method when the observation data reflects a group of players acting in a feedback Nash game.
Learning to Play Trajectory Games Against Opponents with Unknown Objectives
Dec 16, 2022Abstract:Many autonomous agents, such as intelligent vehicles, are inherently required to interact with one another. Game theory provides a natural mathematical tool for robot motion planning in such interactive settings. However, tractable algorithms for such problems usually rely on a strong assumption, namely that the objectives of all players in the scene are known. To make such tools applicable for ego-centric planning with only local information, we propose an adaptive model-predictive game solver, which jointly infers other players' objectives online and computes a corresponding generalized Nash equilibrium (GNE) strategy. The adaptivity of our approach is enabled by a differentiable trajectory game solver whose gradient signal is used for maximum likelihood estimation (MLE) of opponents' objectives. This differentiability of our pipeline facilitates direct integration with other differentiable elements, such as neural networks (NNs). Furthermore, in contrast to existing solvers for cost inference in games, our method handles not only partial state observations but also general inequality constraints. In two simulated traffic scenarios, we find superior performance of our approach over both existing game-theoretic methods and non-game-theoretic model-predictive control (MPC) approaches. We also demonstrate our approach's real-time planning capabilities and robustness in two hardware experiments.
Inferring Objectives in Continuous Dynamic Games from Noise-Corrupted Partial State Observations
Jun 16, 2021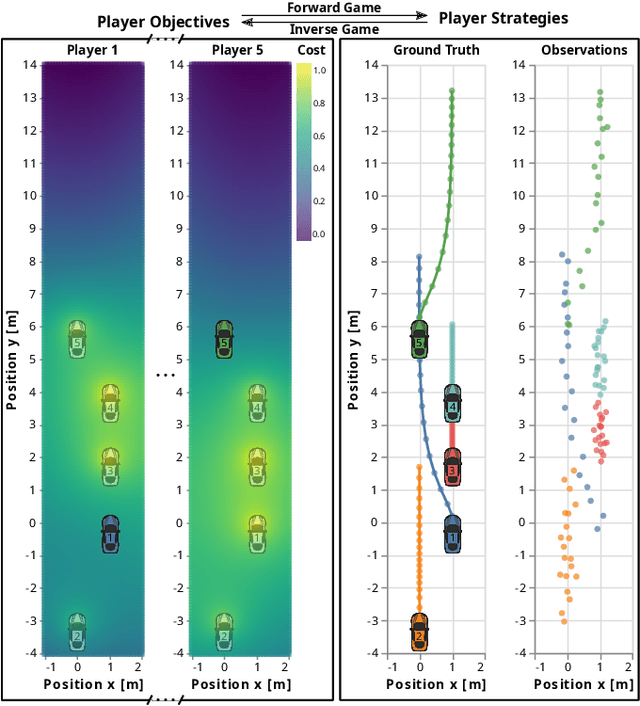

Abstract:Robots and autonomous systems must interact with one another and their environment to provide high-quality services to their users. Dynamic game theory provides an expressive theoretical framework for modeling scenarios involving multiple agents with differing objectives interacting over time. A core challenge when formulating a dynamic game is designing objectives for each agent that capture desired behavior. In this paper, we propose a method for inferring parametric objective models of multiple agents based on observed interactions. Our inverse game solver jointly optimizes player objectives and continuous-state estimates by coupling them through Nash equilibrium constraints. Hence, our method is able to directly maximize the observation likelihood rather than other non-probabilistic surrogate criteria. Our method does not require full observations of game states or player strategies to identify player objectives. Instead, it robustly recovers this information from noisy, partial state observations. As a byproduct of estimating player objectives, our method computes a Nash equilibrium trajectory corresponding to those objectives. Thus, it is suitable for downstream trajectory forecasting tasks. We demonstrate our method in several simulated traffic scenarios. Results show that it reliably estimates player objectives from a short sequence of noise-corrupted partial state observations. Furthermore, using the estimated objectives, our method makes accurate predictions of each player's trajectory.
Inference-Based Strategy Alignment for General-Sum Differential Games
Feb 11, 2020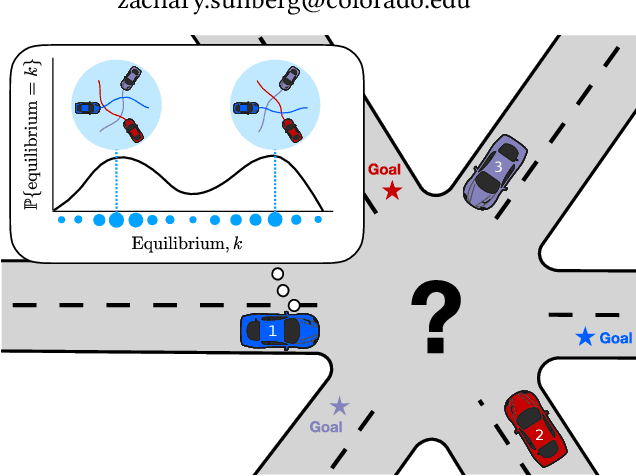

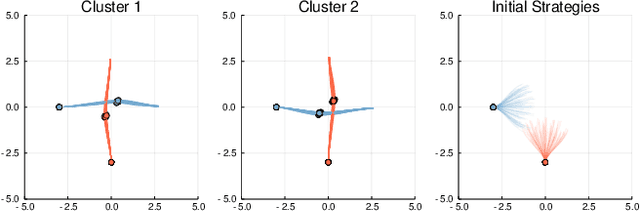
Abstract:In many settings where multiple agents interact, the optimal choices for each agent depend heavily on the choices of the others. These coupled interactions are well-described by a general-sum differential game, in which players have differing objectives, the state evolves in continuous time, and optimal play may be characterized by one of many equilibrium concepts, e.g., a Nash equilibrium. Often, problems admit multiple equilibria. From the perspective of a single agent in such a game, this multiplicity of solutions can introduce uncertainty about how other agents will behave. This paper proposes a general framework for resolving ambiguity between equilibria by reasoning about the equilibrium other agents are aiming for. We demonstrate this framework in simulations of a multi-player human-robot navigation problem that yields two main conclusions: First, by inferring which equilibrium humans are operating at, the robot is able to predict trajectories more accurately, and second, by discovering and aligning itself to this equilibrium the robot is able to reduce the cost for all players.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge