Learning Players' Objectives in Continuous Dynamic Games from Partial State Observations

Robots deployed to the real world must be able to interact with other agents in their environment. Dynamic game theory provides a powerful mathematical framework for modeling scenarios in which agents have individual objectives and interactions evolve over time. However, a key limitation of such techniques is that they require a-priori knowledge of all players' objectives. In this work, we address this issue by proposing a novel method for learning players' objectives in continuous dynamic games from noise-corrupted, partial state observations. Our approach learns objectives by coupling the estimation of unknown cost parameters of each player with inference of unobserved states and inputs through Nash equilibrium constraints. By coupling past state estimates with future state predictions, our approach is amenable to simultaneous online learning and prediction in receding horizon fashion. We demonstrate our method in several simulated traffic scenarios in which we recover players' preferences for, e.g., desired travel speed and collision-avoidance behavior. Results show that our method reliably estimates game-theoretic models from noise-corrupted data that closely matches ground-truth objectives, consistently outperforming state-of-the-art approaches.

Safety and Liveness Guarantees through Reach-Avoid Reinforcement Learning

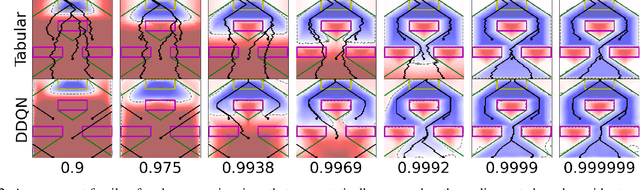
Reach-avoid optimal control problems, in which the system must reach certain goal conditions while staying clear of unacceptable failure modes, are central to safety and liveness assurance for autonomous robotic systems, but their exact solutions are intractable for complex dynamics and environments. Recent successes in reinforcement learning methods to approximately solve optimal control problems with performance objectives make their application to certification problems attractive; however, the Lagrange-type objective used in reinforcement learning is not suitable to encode temporal logic requirements. Recent work has shown promise in extending the reinforcement learning machinery to safety-type problems, whose objective is not a sum, but a minimum (or maximum) over time. In this work, we generalize the reinforcement learning formulation to handle all optimal control problems in the reach-avoid category. We derive a time-discounted reach-avoid Bellman backup with contraction mapping properties and prove that the resulting reach-avoid Q-learning algorithm converges under analogous conditions to the traditional Lagrange-type problem, yielding an arbitrarily tight conservative approximation to the reach-avoid set. We further demonstrate the use of this formulation with deep reinforcement learning methods, retaining zero-violation guarantees by treating the approximate solutions as untrusted oracles in a model-predictive supervisory control framework. We evaluate our proposed framework on a range of nonlinear systems, validating the results against analytic and numerical solutions, and through Monte Carlo simulation in previously intractable problems. Our results open the door to a range of learning-based methods for safe-and-live autonomous behavior, with applications across robotics and automation. See https://github.com/SafeRoboticsLab/safety_rl for code and supplementary material.

Inferring Objectives in Continuous Dynamic Games from Noise-Corrupted Partial State Observations

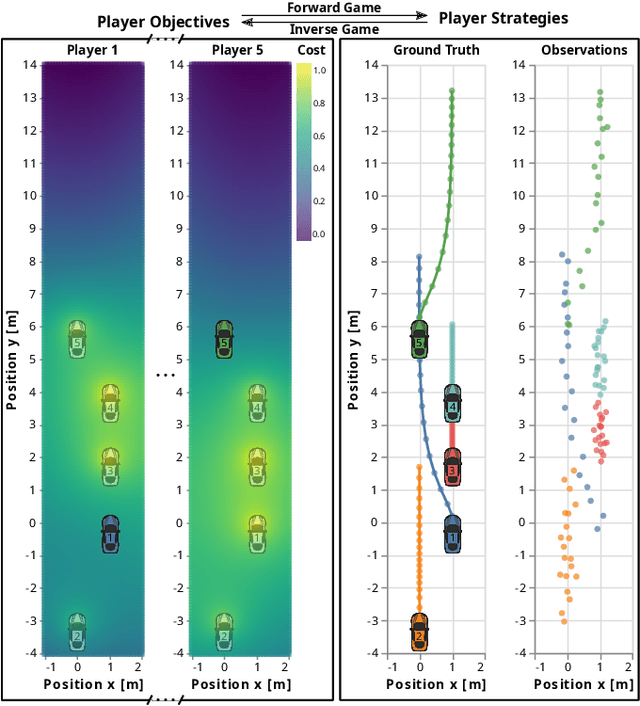
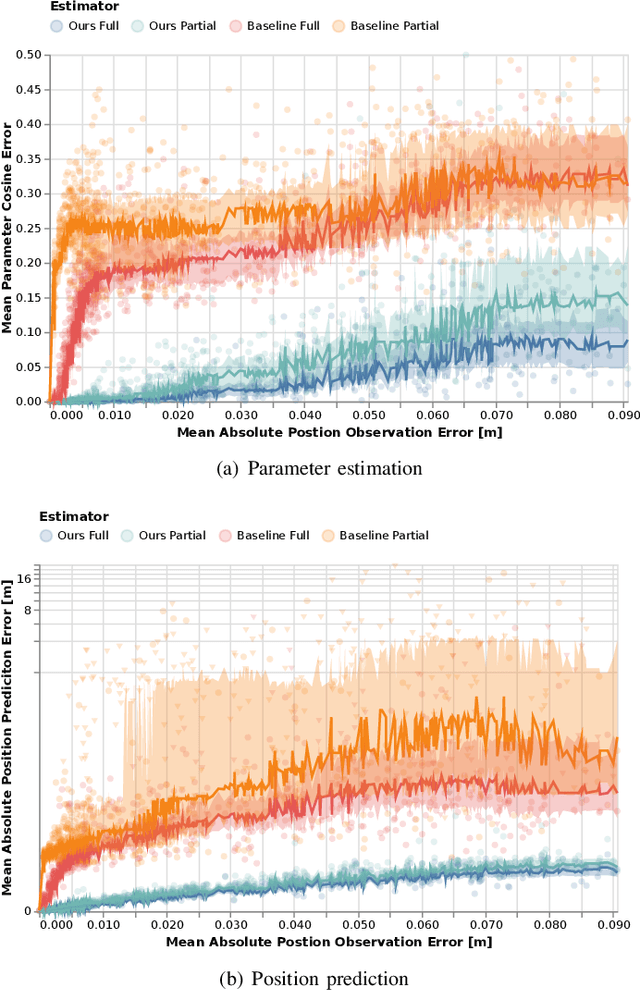
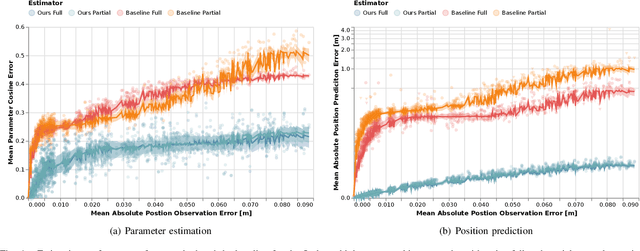
Robots and autonomous systems must interact with one another and their environment to provide high-quality services to their users. Dynamic game theory provides an expressive theoretical framework for modeling scenarios involving multiple agents with differing objectives interacting over time. A core challenge when formulating a dynamic game is designing objectives for each agent that capture desired behavior. In this paper, we propose a method for inferring parametric objective models of multiple agents based on observed interactions. Our inverse game solver jointly optimizes player objectives and continuous-state estimates by coupling them through Nash equilibrium constraints. Hence, our method is able to directly maximize the observation likelihood rather than other non-probabilistic surrogate criteria. Our method does not require full observations of game states or player strategies to identify player objectives. Instead, it robustly recovers this information from noisy, partial state observations. As a byproduct of estimating player objectives, our method computes a Nash equilibrium trajectory corresponding to those objectives. Thus, it is suitable for downstream trajectory forecasting tasks. We demonstrate our method in several simulated traffic scenarios. Results show that it reliably estimates player objectives from a short sequence of noise-corrupted partial state observations. Furthermore, using the estimated objectives, our method makes accurate predictions of each player's trajectory.