A trainable manifold for accurate approximation with ReLU Networks

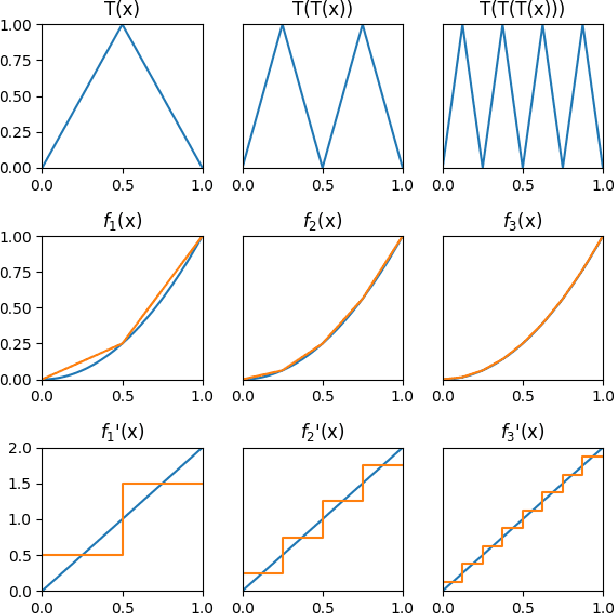
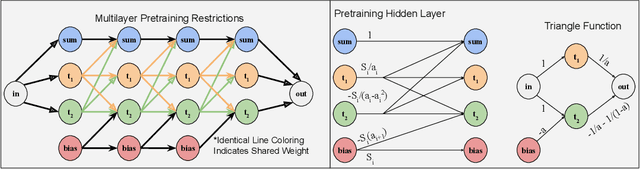
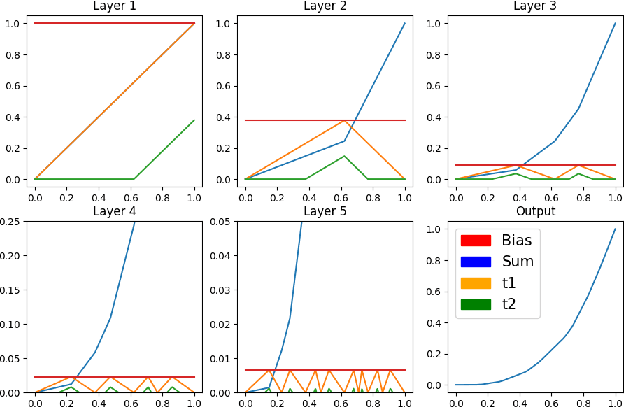
We present a novel technique for exercising greater control of the weights of ReLU activated neural networks to produce more accurate function approximations. Many theoretical works encode complex operations into ReLU networks using smaller base components. In these works, a common base component is a constant width approximation to x^2, which has exponentially decaying error with respect to depth. We extend this block to represent a greater range of convex one-dimensional functions. We derive a manifold of weights such that the output of these new networks utilizes exponentially many piecewise-linear segments. This manifold guides their training process to overcome drawbacks associated with random initialization and unassisted gradient descent. We train these networks to approximate functions which do not necessarily lie on the manifold, showing a significant reduction of error values over conventional approaches.

QTOS: An Open-Source Quadruped Trajectory Optimization Stack

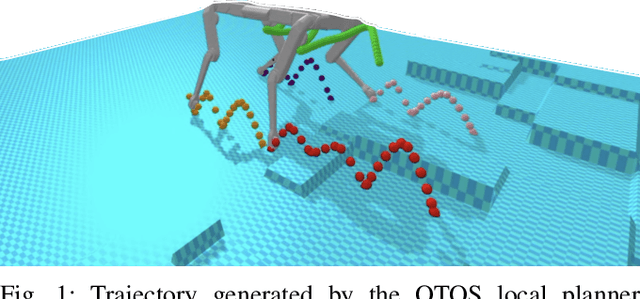
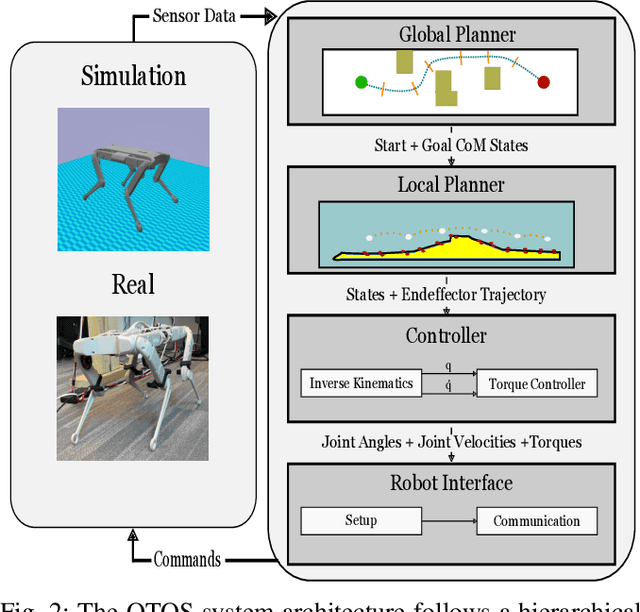
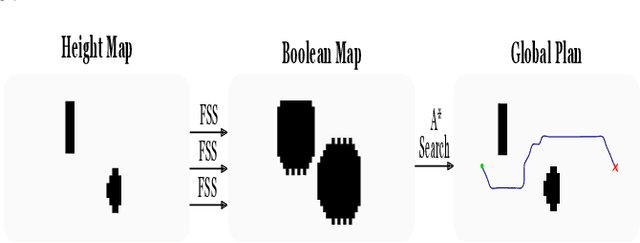
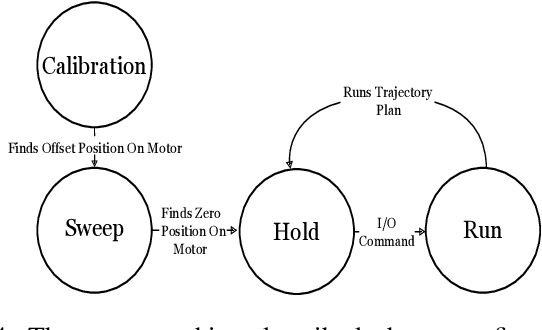
We introduce a new open-source framework, Quadruped Trajectory Optimization Stack (QTOS), which integrates a global planner, local planner, simulator, controller, and robot interface into a single package. QTOS serves as a full-stack interface, simplifying continuous motion planning on an open-source quadruped platform by bridging the gap between middleware and gait planning. It empowers users to effortlessly translate high-level navigation objectives into low-level robot commands. Furthermore, QTOS enhances the stability and adaptability of long-distance gait planning across challenging terrain.

Contingency Games for Multi-Agent Interaction

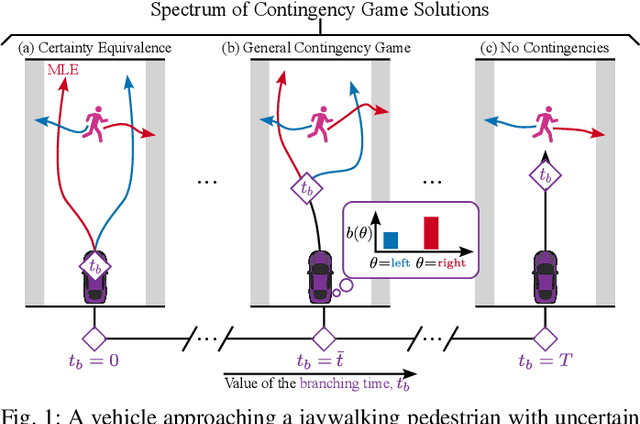
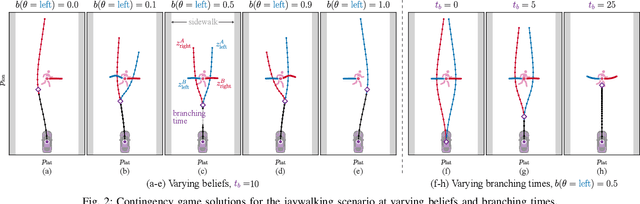
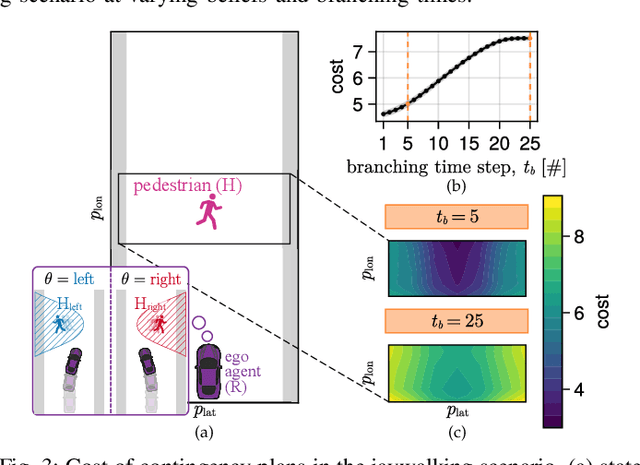
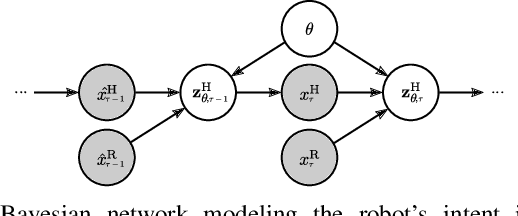
Contingency planning, wherein an agent generates a set of possible plans conditioned on the outcome of an uncertain event, is an increasingly popular way for robots to act under uncertainty. In this work, we take a game-theoretic perspective on contingency planning which is tailored to multi-agent scenarios in which a robot's actions impact the decisions of other agents and vice versa. The resulting contingency game allows the robot to efficiently coordinate with other agents by generating strategic motion plans conditioned on multiple possible intents for other actors in the scene. Contingency games are parameterized via a scalar variable which represents a future time at which intent uncertainty will be resolved. Varying this parameter enables a designer to easily adjust how conservatively the robot behaves in the game. Interestingly, we also find that existing variants of game-theoretic planning under uncertainty are readily obtained as special cases of contingency games. Lastly, we offer an efficient method for solving N-player contingency games with nonlinear dynamics and non-convex costs and constraints. Through a series of simulated autonomous driving scenarios, we demonstrate that plans generated via contingency games provide quantitative performance gains over game-theoretic motion plans that do not account for future uncertainty reduction.

Incorporating Data Uncertainty in Object Tracking Algorithms

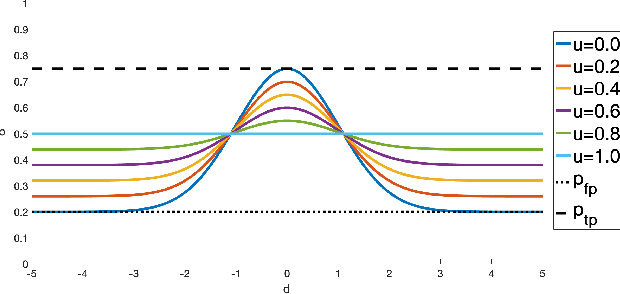
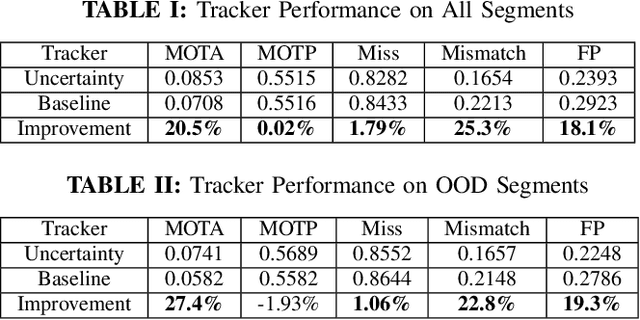
Methodologies for incorporating the uncertainties characteristic of data-driven object detectors into object tracking algorithms are explored. Object tracking methods rely on measurement error models, typically in the form of measurement noise, false positive rates, and missed detection rates. Each of these quantities, in general, can be dependent on object or measurement location. However, for detections generated from neural-network processed camera inputs, these measurement error statistics are not sufficient to represent the primary source of errors, namely a dissimilarity between run-time sensor input and the training data upon which the detector was trained. To this end, we investigate incorporating data uncertainty into object tracking methods such as to improve the ability to track objects, and particularly those which out-of-distribution w.r.t. training data. The proposed methodologies are validated on an object tracking benchmark as well on experiments with a real autonomous aircraft.

The Computation of Approximate Generalized Feedback Nash Equilibria

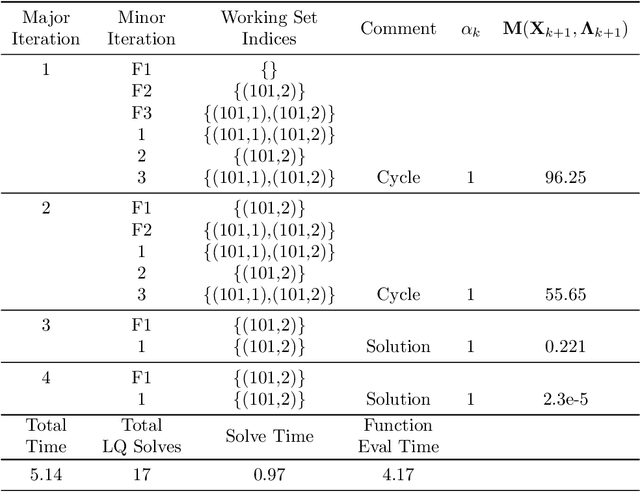
We present the concept of a Generalized Feedback Nash Equilibrium (GFNE) in dynamic games, extending the Feedback Nash Equilibrium concept to games in which players are subject to state and input constraints. We formalize necessary and sufficient conditions for (local) GFNE solutions at the trajectory level, which enable the development of efficient numerical methods for their computation. Specifically, we propose a Newton-style method for finding game trajectories which satisfy the necessary conditions, which can then be checked against the sufficiency conditions. We show that the evaluation of the necessary conditions in general requires computing a series of nested, implicitly-defined derivatives, which quickly becomes intractable. To this end, we introduce an approximation to the necessary conditions which is amenable to efficient evaluation, and in turn, computation of solutions. We term the solutions to the approximate necessary conditions Generalized Feedback Quasi Nash Equilibria (GFQNE), and we introduce numerical methods for their computation. In particular, we develop a Sequential Linear-Quadratic Game approach, in which a locally approximate LQ game is solved at each iteration. The development of this method relies on the ability to compute a GFNE to inequality- and equality-constrained LQ games, and therefore specific methods for the solution of these special cases are developed in detail. We demonstrate the effectiveness of the proposed solution approach on a dynamic game arising in an autonomous driving application.

Multi-Hypothesis Interactions in Game-Theoretic Motion Planning

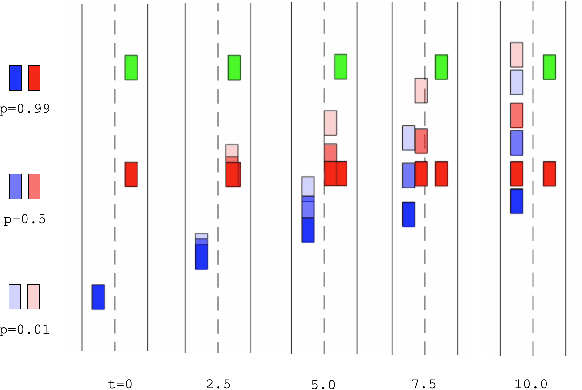
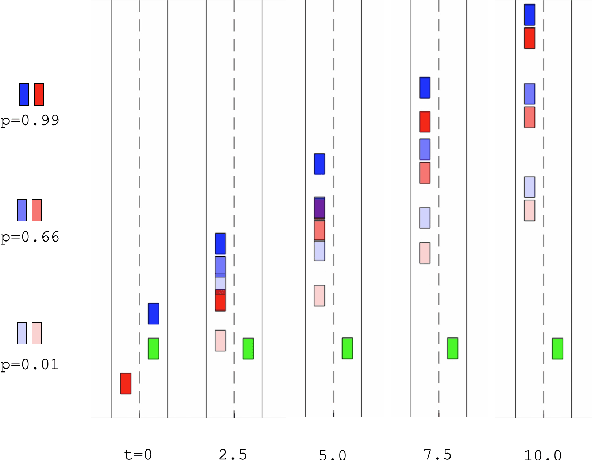
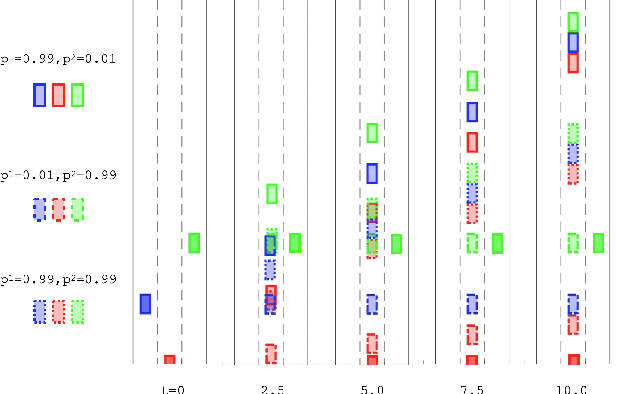
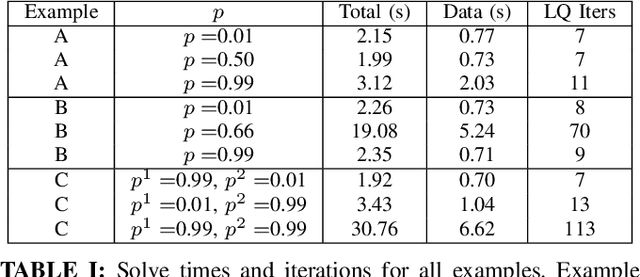
We present a novel method for handling uncertainty about the intentions of non-ego players in dynamic games, with application to motion planning for autonomous vehicles. Equilibria in these games explicitly account for interaction among other agents in the environment, such as drivers and pedestrians. Our method models the uncertainty about the intention of other agents by constructing multiple hypotheses about the objectives and constraints of other agents in the scene. For each candidate hypothesis, we associate a Bernoulli random variable representing the probability of that hypothesis, which may or may not be independent of the probability of other hypotheses. We leverage constraint asymmetries and feedback information patterns to incorporate the probabilities of hypotheses in a natural way. Specifically, increasing the probability associated with a given hypothesis from $0$ to $1$ shifts the responsibility of collision avoidance from the hypothesized agent to the ego agent. This method allows the generation of interactive trajectories for the ego agent, where the level of assertiveness or caution that the ego exhibits is directly related to the easy-to-model uncertainty it maintains about the scene.

Testing for Typicality with Respect to an Ensemble of Learned Distributions

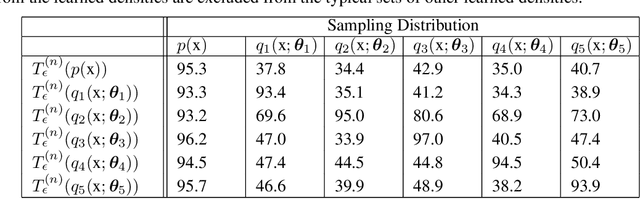
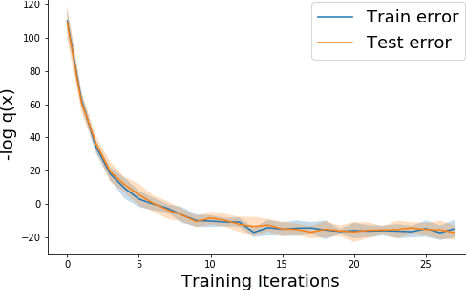
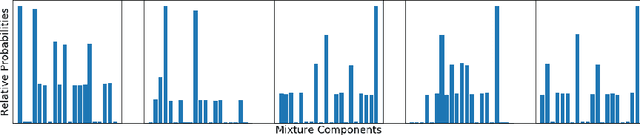
Methods of performing anomaly detection on high-dimensional data sets are needed, since algorithms which are trained on data are only expected to perform well on data that is similar to the training data. There are theoretical results on the ability to detect if a population of data is likely to come from a known base distribution, which is known as the goodness-of-fit problem. One-sample approaches to this problem offer significant computational advantages for online testing, but require knowing a model of the base distribution. The ability to correctly reject anomalous data in this setting hinges on the accuracy of the model of the base distribution. For high dimensional data, learning an accurate-enough model of the base distribution such that anomaly detection works reliably is very challenging, as many researchers have noted in recent years. Existing methods for the one-sample goodness-of-fit problem do not account for the fact that a model of the base distribution is learned. To address that gap, we offer a theoretically motivated approach to account for the density learning procedure. In particular, we propose training an ensemble of density models, considering data to be anomalous if the data is anomalous with respect to any member of the ensemble. We provide a theoretical justification for this approach, proving first that a test on typicality is a valid approach to the goodness-of-fit problem, and then proving that for a correctly constructed ensemble of models, the intersection of typical sets of the models lies in the interior of the typical set of the base distribution. We present our method in the context of an example on synthetic data in which the effects we consider can easily be seen.

Real-time Funnel Generation for Restricted Motion Planning

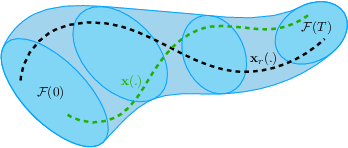
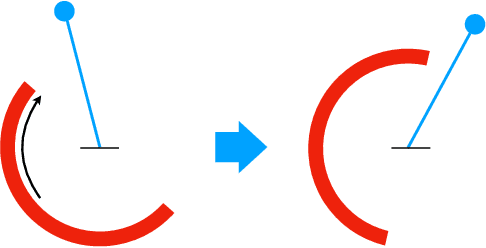
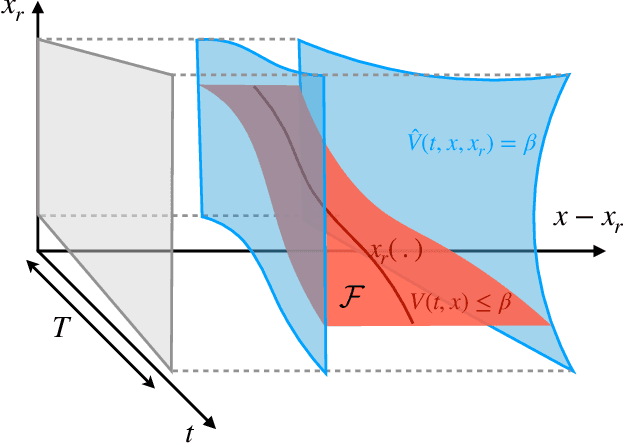
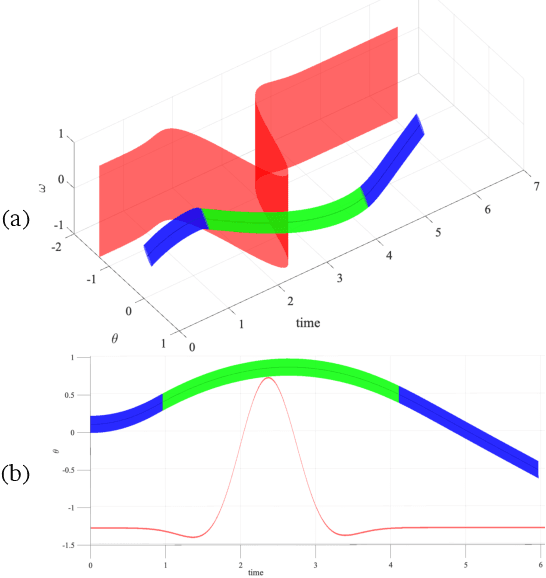
In autonomous systems, a motion planner generates reference trajectories which are tracked by a low-level controller. For safe operation, the motion planner should account for inevitable controller tracking error when generating avoidance trajectories. In this article we present a method for generating provably safe tracking error bounds, while reducing over-conservatism that exists in existing methods. We achieve this goal by restricting possible behaviors for the motion planner. We provide an algebraic method based on sum-of-squares programming to define restrictions on the motion planner and find small bounds on the tracking error. We demonstrate our method on two case studies and show how we can integrate the method into already developed motion planning techniques. Results suggest that our method can provide acceptable tracking error wherein previous work were not applicable.

The Parallelization of Riccati Recursion

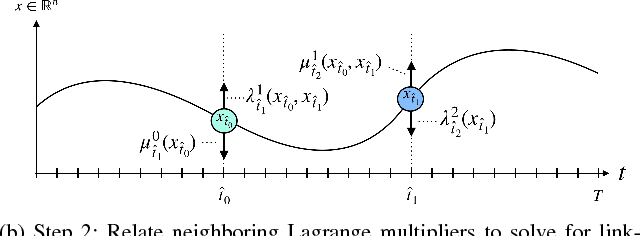
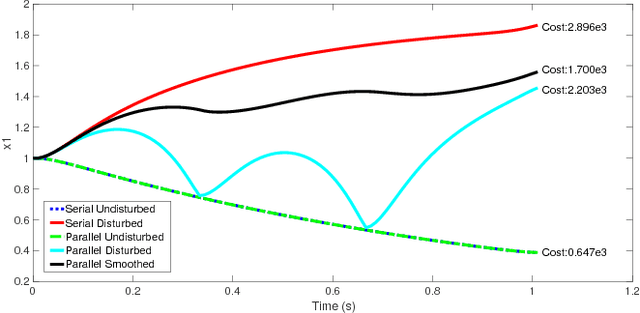
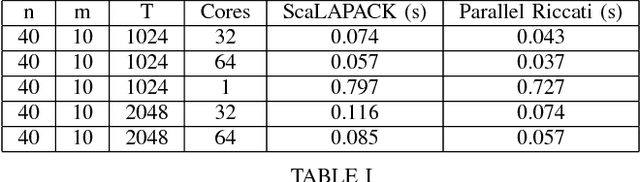
A method is presented for parallelizing the computation of solutions to discrete-time, linear-quadratic, finite-horizon optimal control problems, which we will refer to as LQR problems. This class of problem arises frequently in robotic trajectory optimization. For very complicated robots, the size of these resulting problems can be large enough that computing the solution is prohibitively slow when using a single processor. Fortunately, approaches to solving these type of problems based on numerical solutions to the KKT conditions of optimality offer a parallel solution method and can leverage multiple processors to compute solutions faster. However, these methods do not produce the useful feedback control policies that are generated as a by-product of the dynamic-programming solution method known as Riccati recursion. In this paper we derive a method which is able to parallelize the computation of Riccati recursion, allowing for super-fast solutions to the LQR problem while still generating feedback control policies. We demonstrate empirically that our method is faster than existing parallel methods.

Learning Quadrotor Dynamics Using Neural Network for Flight Control

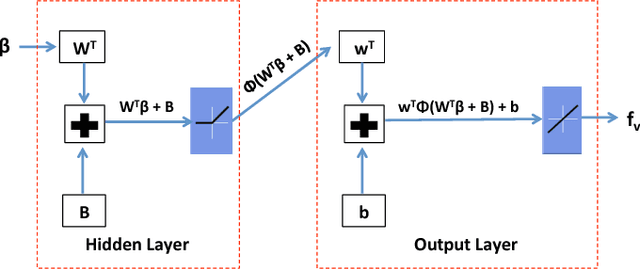
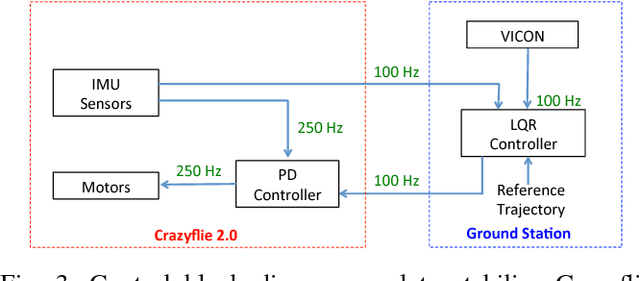
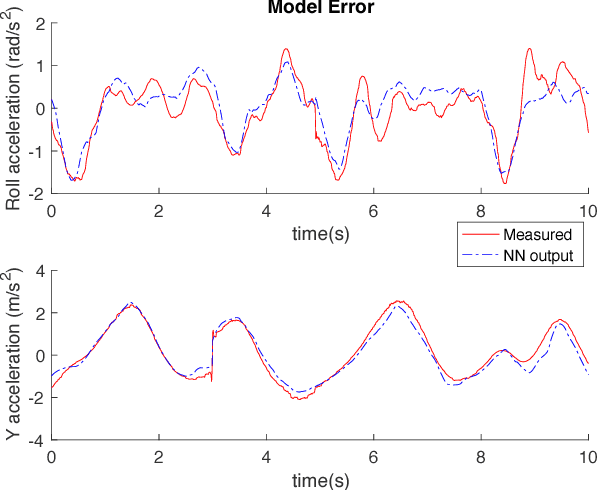
Traditional learning approaches proposed for controlling quadrotors or helicopters have focused on improving performance for specific trajectories by iteratively improving upon a nominal controller, for example learning from demonstrations, iterative learning, and reinforcement learning. In these schemes, however, it is not clear how the information gathered from the training trajectories can be used to synthesize controllers for more general trajectories. Recently, the efficacy of deep learning in inferring helicopter dynamics has been shown. Motivated by the generalization capability of deep learning, this paper investigates whether a neural network based dynamics model can be employed to synthesize control for trajectories different than those used for training. To test this, we learn a quadrotor dynamics model using only translational and only rotational training trajectories, each of which can be controlled independently, and then use it to simultaneously control the yaw and position of a quadrotor, which is non-trivial because of nonlinear couplings between the two motions. We validate our approach in experiments on a quadrotor testbed.