Testing for Typicality with Respect to an Ensemble of Learned Distributions

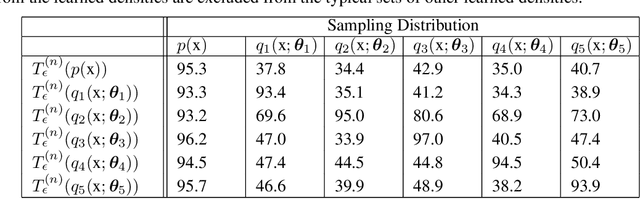
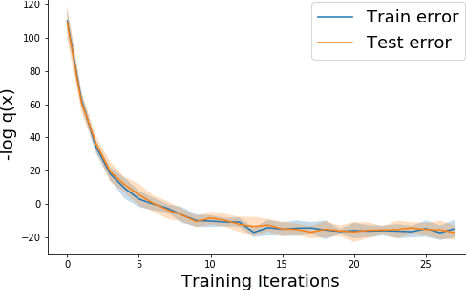
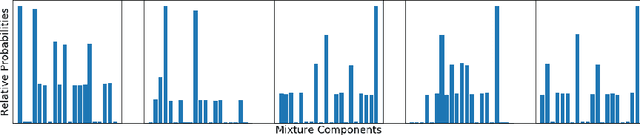
Methods of performing anomaly detection on high-dimensional data sets are needed, since algorithms which are trained on data are only expected to perform well on data that is similar to the training data. There are theoretical results on the ability to detect if a population of data is likely to come from a known base distribution, which is known as the goodness-of-fit problem. One-sample approaches to this problem offer significant computational advantages for online testing, but require knowing a model of the base distribution. The ability to correctly reject anomalous data in this setting hinges on the accuracy of the model of the base distribution. For high dimensional data, learning an accurate-enough model of the base distribution such that anomaly detection works reliably is very challenging, as many researchers have noted in recent years. Existing methods for the one-sample goodness-of-fit problem do not account for the fact that a model of the base distribution is learned. To address that gap, we offer a theoretically motivated approach to account for the density learning procedure. In particular, we propose training an ensemble of density models, considering data to be anomalous if the data is anomalous with respect to any member of the ensemble. We provide a theoretical justification for this approach, proving first that a test on typicality is a valid approach to the goodness-of-fit problem, and then proving that for a correctly constructed ensemble of models, the intersection of typical sets of the models lies in the interior of the typical set of the base distribution. We present our method in the context of an example on synthetic data in which the effects we consider can easily be seen.