A Minimum Discounted Reward Hamilton-Jacobi Formulation for Computing Reachable Sets

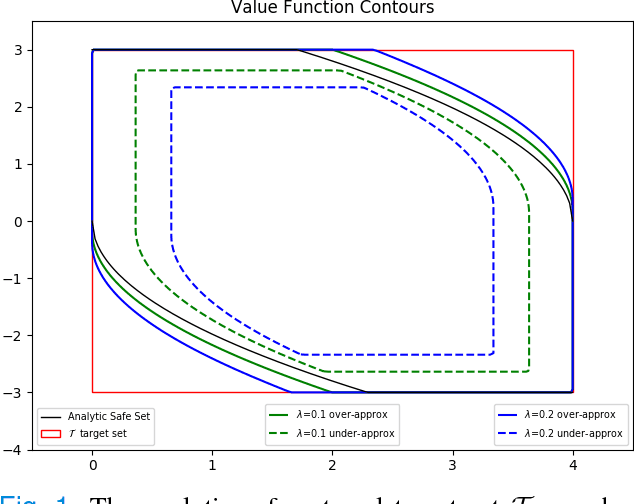
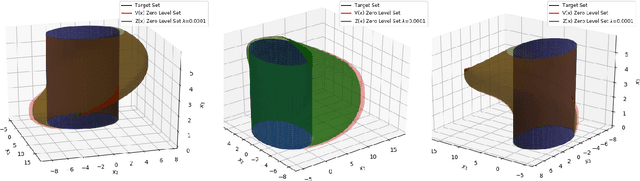
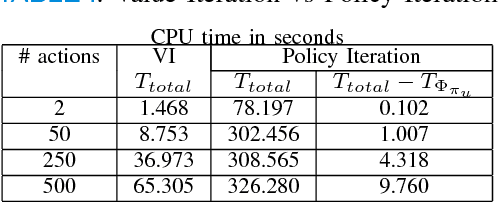
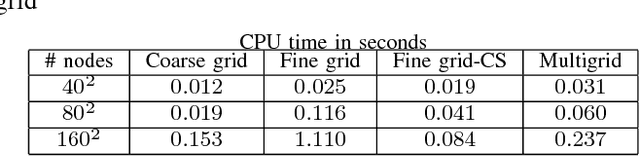
We propose a novel formulation for approximating reachable sets through a minimum discounted reward optimal control problem. The formulation yields a continuous solution that can be obtained by solving a Hamilton-Jacobi equation. Furthermore, the numerical approximation to this solution can be obtained as the unique fixed-point to a contraction mapping. This allows for more efficient solution methods that could not be applied under traditional formulations for solving reachable sets. In addition, this formulation provides a link between reinforcement learning and learning reachable sets for systems with unknown dynamics, allowing algorithms from the former to be applied to the latter. We use two benchmark examples, double integrator, and pursuit-evasion games, to show the correctness of the formulation as well as its strengths in comparison to previous work.

A General Safety Framework for Learning-Based Control in Uncertain Robotic Systems

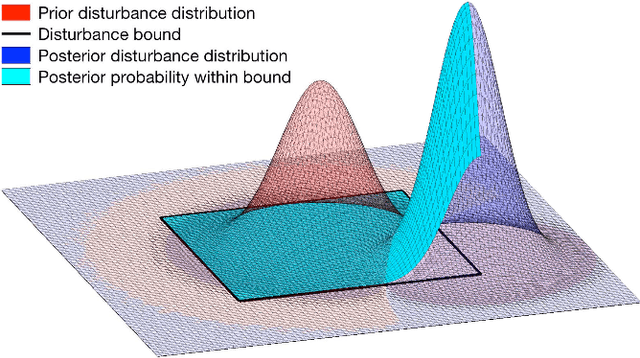
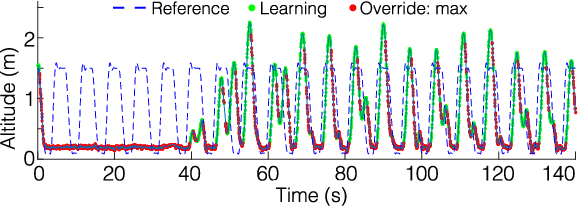
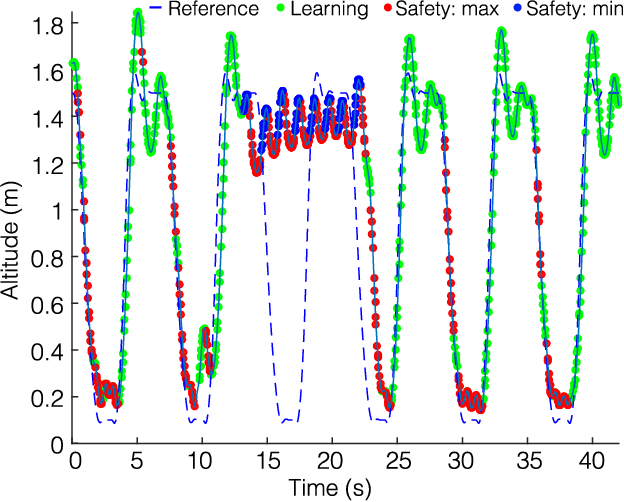
The proven efficacy of learning-based control schemes strongly motivates their application to robotic systems operating in the physical world. However, guaranteeing correct operation during the learning process is currently an unresolved issue, which is of vital importance in safety-critical systems. We propose a general safety framework based on Hamilton-Jacobi reachability methods that can work in conjunction with an arbitrary learning algorithm. The method exploits approximate knowledge of the system dynamics to guarantee constraint satisfaction while minimally interfering with the learning process. We further introduce a Bayesian mechanism that refines the safety analysis as the system acquires new evidence, reducing initial conservativeness when appropriate while strengthening guarantees through real-time validation. The result is a least-restrictive, safety-preserving control law that intervenes only when (a) the computed safety guarantees require it, or (b) confidence in the computed guarantees decays in light of new observations. We prove theoretical safety guarantees combining probabilistic and worst-case analysis and demonstrate the proposed framework experimentally on a quadrotor vehicle. Even though safety analysis is based on a simple point-mass model, the quadrotor successfully arrives at a suitable controller by policy-gradient reinforcement learning without ever crashing, and safely retracts away from a strong external disturbance introduced during flight.

Learning Quadrotor Dynamics Using Neural Network for Flight Control

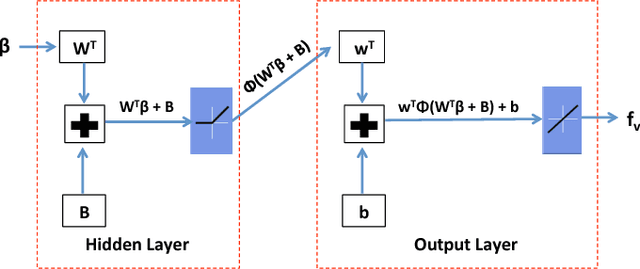
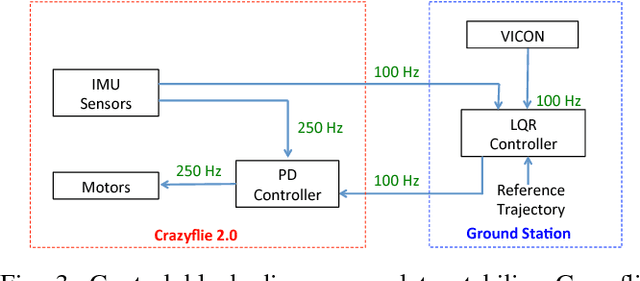
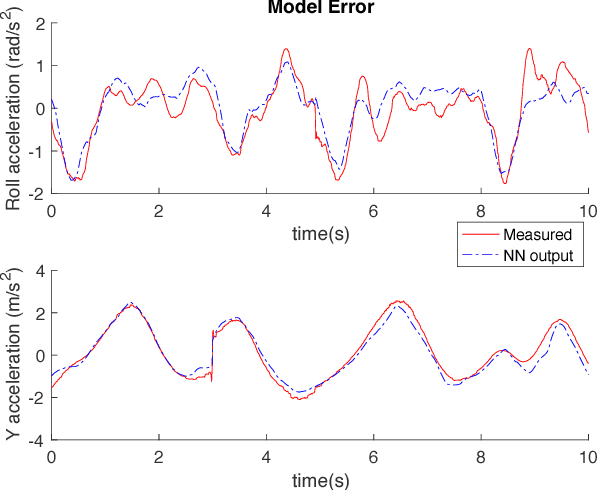
Traditional learning approaches proposed for controlling quadrotors or helicopters have focused on improving performance for specific trajectories by iteratively improving upon a nominal controller, for example learning from demonstrations, iterative learning, and reinforcement learning. In these schemes, however, it is not clear how the information gathered from the training trajectories can be used to synthesize controllers for more general trajectories. Recently, the efficacy of deep learning in inferring helicopter dynamics has been shown. Motivated by the generalization capability of deep learning, this paper investigates whether a neural network based dynamics model can be employed to synthesize control for trajectories different than those used for training. To test this, we learn a quadrotor dynamics model using only translational and only rotational training trajectories, each of which can be controlled independently, and then use it to simultaneously control the yaw and position of a quadrotor, which is non-trivial because of nonlinear couplings between the two motions. We validate our approach in experiments on a quadrotor testbed.