A General Safety Framework for Learning-Based Control in Uncertain Robotic Systems

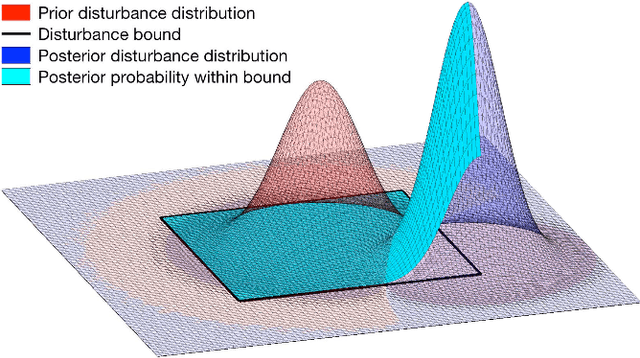
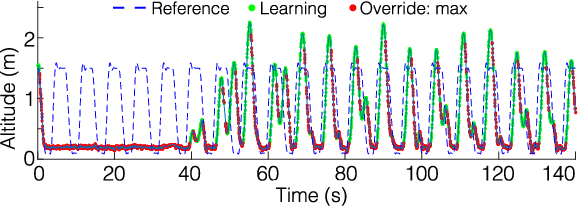
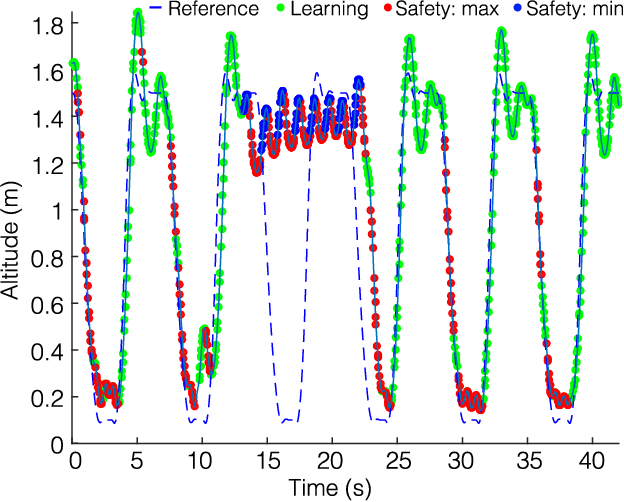
The proven efficacy of learning-based control schemes strongly motivates their application to robotic systems operating in the physical world. However, guaranteeing correct operation during the learning process is currently an unresolved issue, which is of vital importance in safety-critical systems. We propose a general safety framework based on Hamilton-Jacobi reachability methods that can work in conjunction with an arbitrary learning algorithm. The method exploits approximate knowledge of the system dynamics to guarantee constraint satisfaction while minimally interfering with the learning process. We further introduce a Bayesian mechanism that refines the safety analysis as the system acquires new evidence, reducing initial conservativeness when appropriate while strengthening guarantees through real-time validation. The result is a least-restrictive, safety-preserving control law that intervenes only when (a) the computed safety guarantees require it, or (b) confidence in the computed guarantees decays in light of new observations. We prove theoretical safety guarantees combining probabilistic and worst-case analysis and demonstrate the proposed framework experimentally on a quadrotor vehicle. Even though safety analysis is based on a simple point-mass model, the quadrotor successfully arrives at a suitable controller by policy-gradient reinforcement learning without ever crashing, and safely retracts away from a strong external disturbance introduced during flight.

A sampling-based approach to scalable constraint satisfaction in linear sampled-data systems---Part I: Computation

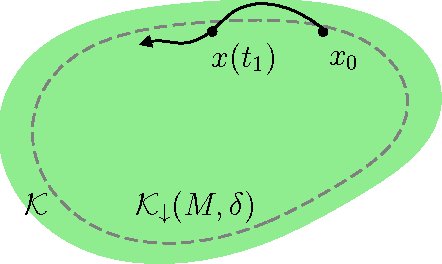
Sampled-data (SD) systems, which are composed of both discrete- and continuous-time components, are arguably one of the most common classes of cyberphysical systems in practice; most modern controllers are implemented on digital platforms while the plant dynamics that are being controlled evolve continuously in time. As with all cyberphysical systems, ensuring hard constraint satisfaction is key in the safe operation of SD systems. A powerful analytical tool for guaranteeing such constraint satisfaction is the viability kernel: the set of all initial conditions for which a safety-preserving control law (that is, a control law that satisfies all input and state constraints) exists. In this paper we present a novel sampling-based algorithm that tightly approximates the viability kernel for high-dimensional sampled-data linear time-invariant (LTI) systems. Unlike prior work in this area, our algorithm formally handles both the discrete and continuous characteristics of SD systems. We prove the correctness and convergence of our approximation technique, provide discussions on heuristic methods to optimally bias the sampling process, and demonstrate the results on a twelve-dimensional flight envelope protection problem.