A sampling-based approach to scalable constraint satisfaction in linear sampled-data systems---Part I: Computation
Paper and Code
May 09, 2014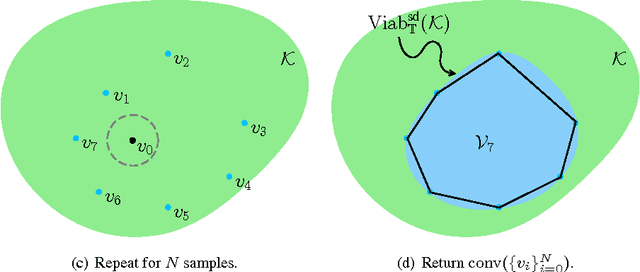
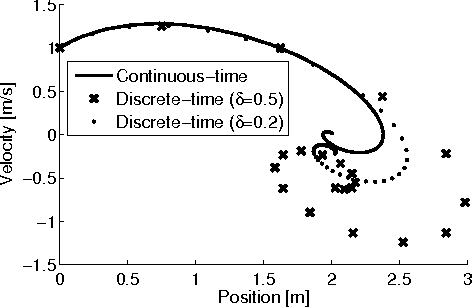
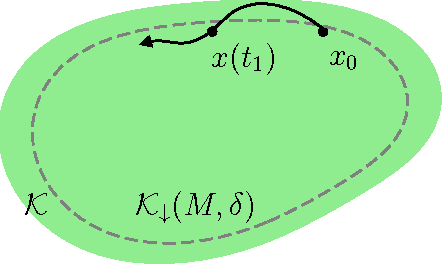
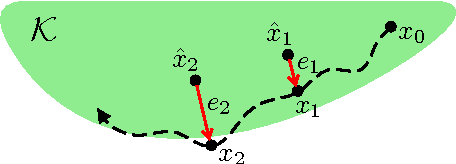
Sampled-data (SD) systems, which are composed of both discrete- and continuous-time components, are arguably one of the most common classes of cyberphysical systems in practice; most modern controllers are implemented on digital platforms while the plant dynamics that are being controlled evolve continuously in time. As with all cyberphysical systems, ensuring hard constraint satisfaction is key in the safe operation of SD systems. A powerful analytical tool for guaranteeing such constraint satisfaction is the viability kernel: the set of all initial conditions for which a safety-preserving control law (that is, a control law that satisfies all input and state constraints) exists. In this paper we present a novel sampling-based algorithm that tightly approximates the viability kernel for high-dimensional sampled-data linear time-invariant (LTI) systems. Unlike prior work in this area, our algorithm formally handles both the discrete and continuous characteristics of SD systems. We prove the correctness and convergence of our approximation technique, provide discussions on heuristic methods to optimally bias the sampling process, and demonstrate the results on a twelve-dimensional flight envelope protection problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge