A General Safety Framework for Learning-Based Control in Uncertain Robotic Systems
Paper and Code
Feb 14, 2018
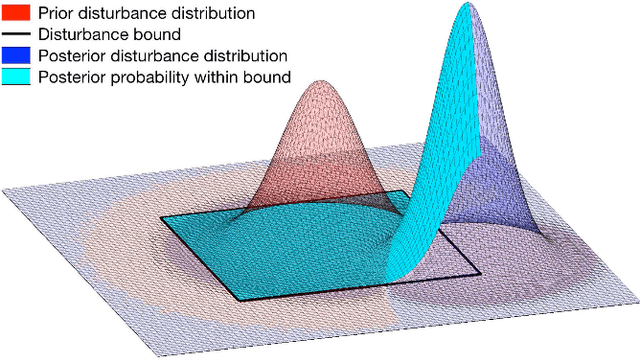
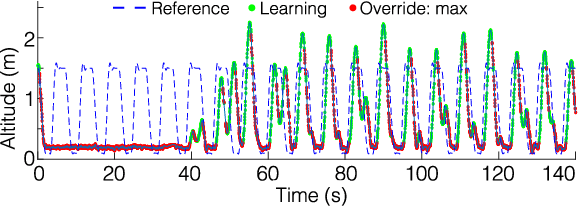
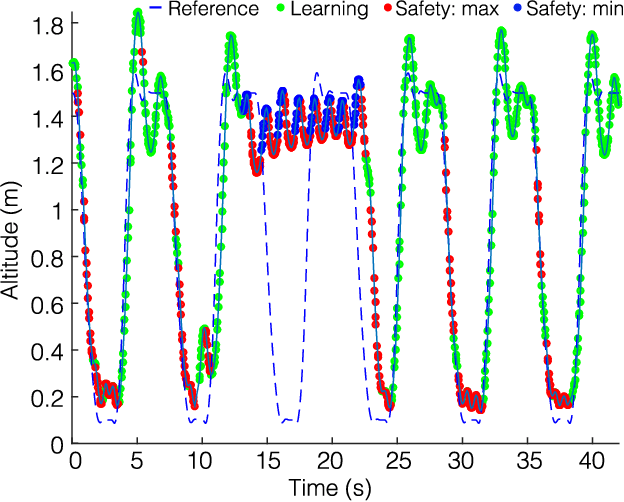
The proven efficacy of learning-based control schemes strongly motivates their application to robotic systems operating in the physical world. However, guaranteeing correct operation during the learning process is currently an unresolved issue, which is of vital importance in safety-critical systems. We propose a general safety framework based on Hamilton-Jacobi reachability methods that can work in conjunction with an arbitrary learning algorithm. The method exploits approximate knowledge of the system dynamics to guarantee constraint satisfaction while minimally interfering with the learning process. We further introduce a Bayesian mechanism that refines the safety analysis as the system acquires new evidence, reducing initial conservativeness when appropriate while strengthening guarantees through real-time validation. The result is a least-restrictive, safety-preserving control law that intervenes only when (a) the computed safety guarantees require it, or (b) confidence in the computed guarantees decays in light of new observations. We prove theoretical safety guarantees combining probabilistic and worst-case analysis and demonstrate the proposed framework experimentally on a quadrotor vehicle. Even though safety analysis is based on a simple point-mass model, the quadrotor successfully arrives at a suitable controller by policy-gradient reinforcement learning without ever crashing, and safely retracts away from a strong external disturbance introduced during flight.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge