A trainable manifold for accurate approximation with ReLU Networks

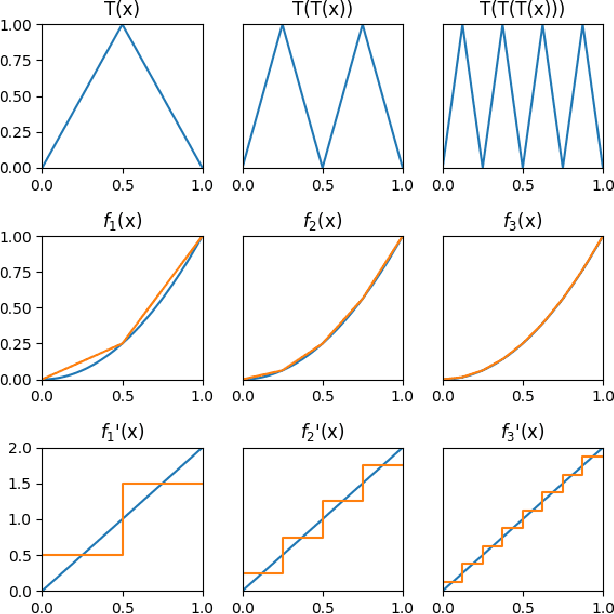
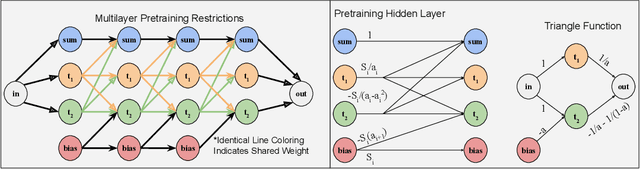
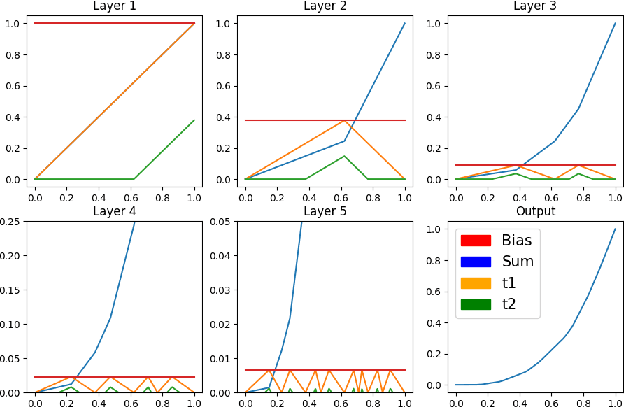
We present a novel technique for exercising greater control of the weights of ReLU activated neural networks to produce more accurate function approximations. Many theoretical works encode complex operations into ReLU networks using smaller base components. In these works, a common base component is a constant width approximation to x^2, which has exponentially decaying error with respect to depth. We extend this block to represent a greater range of convex one-dimensional functions. We derive a manifold of weights such that the output of these new networks utilizes exponentially many piecewise-linear segments. This manifold guides their training process to overcome drawbacks associated with random initialization and unassisted gradient descent. We train these networks to approximate functions which do not necessarily lie on the manifold, showing a significant reduction of error values over conventional approaches.