Policies with Sparse Inter-Agent Dependencies in Dynamic Games: A Dynamic Programming Approach

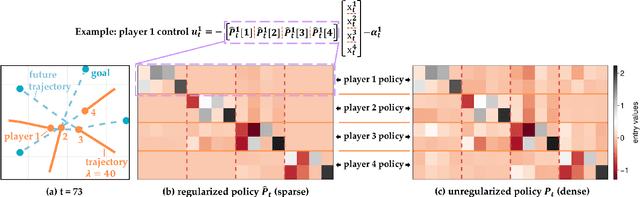
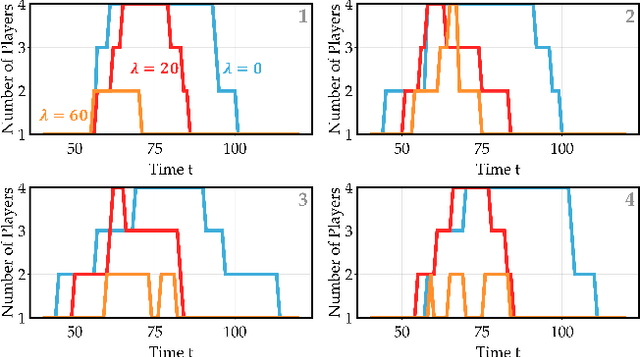
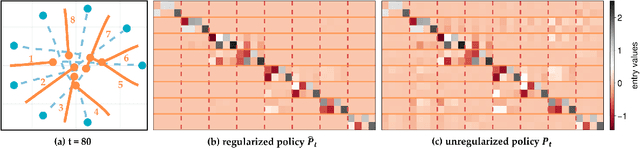
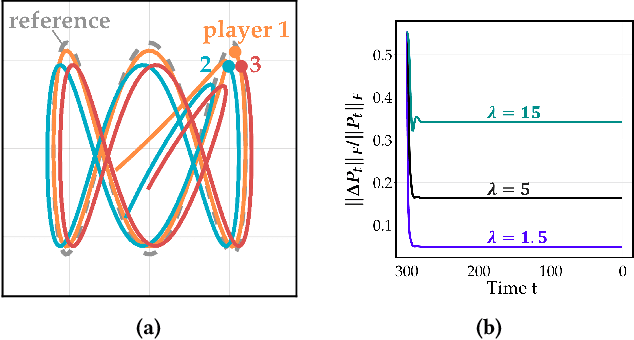
Common feedback strategies in multi-agent dynamic games require all players' state information to compute control strategies. However, in real-world scenarios, sensing and communication limitations between agents make full state feedback expensive or impractical, and such strategies can become fragile when state information from other agents is inaccurate. To this end, we propose a regularized dynamic programming approach for finding sparse feedback policies that selectively depend on the states of a subset of agents in dynamic games. The proposed approach solves convex adaptive group Lasso problems to compute sparse policies approximating Nash equilibrium solutions. We prove the regularized solutions' asymptotic convergence to a neighborhood of Nash equilibrium policies in linear-quadratic (LQ) games. We extend the proposed approach to general non-LQ games via an iterative algorithm. Empirical results in multi-robot interaction scenarios show that the proposed approach effectively computes feedback policies with varying sparsity levels. When agents have noisy observations of other agents' states, simulation results indicate that the proposed regularized policies consistently achieve lower costs than standard Nash equilibrium policies by up to 77% for all interacting agents whose costs are coupled with other agents' states.

Solving Reach-Avoid-Stay Problems Using Deep Deterministic Policy Gradients

Reach-Avoid-Stay (RAS) optimal control enables systems such as robots and air taxis to reach their targets, avoid obstacles, and stay near the target. However, current methods for RAS often struggle with handling complex, dynamic environments and scaling to high-dimensional systems. While reinforcement learning (RL)-based reachability analysis addresses these challenges, it has yet to tackle the RAS problem. In this paper, we propose a two-step deep deterministic policy gradient (DDPG) method to extend RL-based reachability method to solve RAS problems. First, we train a function that characterizes the maximal robust control invariant set within the target set, where the system can safely stay, along with its corresponding policy. Second, we train a function that defines the set of states capable of safely reaching the robust control invariant set, along with its corresponding policy. We prove that this method results in the maximal robust RAS set in the absence of training errors and demonstrate that it enables RAS in complex environments, scales to high-dimensional systems, and achieves higher success rates for the RAS task compared to previous methods, validated through one simulation and two high-dimensional experiments.

Constraint Inference in Control Tasks from Expert Demonstrations via Inverse Optimization

Inferring unknown constraints is a challenging and crucial problem in many robotics applications. When only expert demonstrations are available, it becomes essential to infer the unknown domain constraints to deploy additional agents effectively. In this work, we propose an approach to infer affine constraints in control tasks after observing expert demonstrations. We formulate the constraint inference problem as an inverse optimization problem, and we propose an alternating optimization scheme that infers the unknown constraints by minimizing a KKT residual objective. We demonstrate the effectiveness of our method in a number of simulations, and show that our method can infer less conservative constraints than a recent baseline method while maintaining comparable safety guarantees.

Cost Inference for Feedback Dynamic Games from Noisy Partial State Observations and Incomplete Trajectories

In multi-agent dynamic games, the Nash equilibrium state trajectory of each agent is determined by its cost function and the information pattern of the game. However, the cost and trajectory of each agent may be unavailable to the other agents. Prior work on using partial observations to infer the costs in dynamic games assumes an open-loop information pattern. In this work, we demonstrate that the feedback Nash equilibrium concept is more expressive and encodes more complex behavior. It is desirable to develop specific tools for inferring players' objectives in feedback games. Therefore, we consider the dynamic game cost inference problem under the feedback information pattern, using only partial state observations and incomplete trajectory data. To this end, we first propose an inverse feedback game loss function, whose minimizer yields a feedback Nash equilibrium state trajectory closest to the observation data. We characterize the landscape and differentiability of the loss function. Given the difficulty of obtaining the exact gradient, our main contribution is an efficient gradient approximator, which enables a novel inverse feedback game solver that minimizes the loss using first-order optimization. In thorough empirical evaluations, we demonstrate that our algorithm converges reliably and has better robustness and generalization performance than the open-loop baseline method when the observation data reflects a group of players acting in a feedback Nash game.

Forget Less, Count Better: A Domain-Incremental Self-Distillation Learning Benchmark for Lifelong Crowd Counting

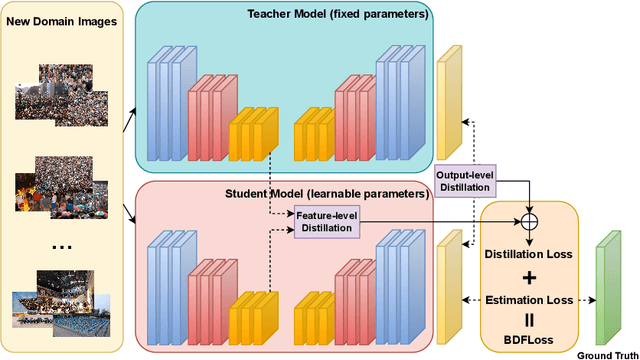
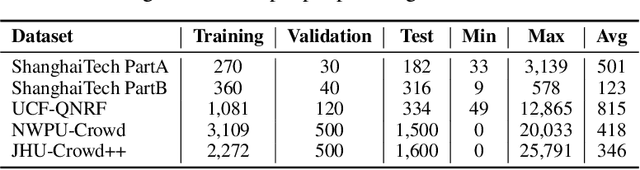
Crowd Counting has important applications in public safety and pandemic control. A robust and practical crowd counting system has to be capable of continuously learning with the new-coming domain data in real-world scenarios instead of fitting one domain only. Off-the-shelf methods have some drawbacks to handle multiple domains. 1) The models will achieve limited performance (even drop dramatically) among old domains after training images from new domains due to the discrepancies of intrinsic data distributions from various domains, which is called catastrophic forgetting. 2) The well-trained model in a specific domain achieves imperfect performance among other unseen domains because of the domain shift. 3) It leads to linearly-increased storage overhead either mixing all the data for training or simply training dozens of separate models for different domains when new ones are available. To overcome these issues, we investigate a new task of crowd counting under the incremental domains training setting, namely, Lifelong Crowd Counting. It aims at alleviating the catastrophic forgetting and improving the generalization ability using a single model updated by the incremental domains. To be more specific, we propose a self-distillation learning framework as a benchmark~(Forget Less, Count Better, FLCB) for lifelong crowd counting, which helps the model sustainably leverage previous meaningful knowledge for better crowd counting to mitigate the forgetting when the new data arrive. Meanwhile, a new quantitative metric, normalized backward transfer~(nBwT), is developed to evaluate the forgetting degree of the model in the lifelong learning process. Extensive experimental results demonstrate the superiority of our proposed benchmark in achieving a low catastrophic forgetting degree and strong generalization ability.

Infinite-Horizon Reach-Avoid Zero-Sum Games via Deep Reinforcement Learning

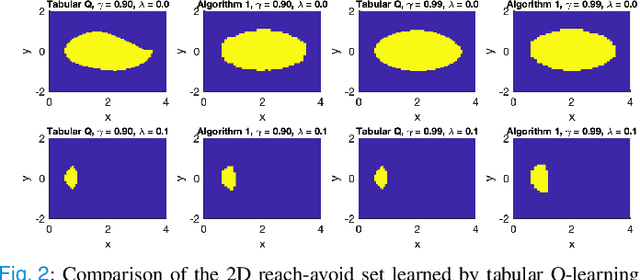
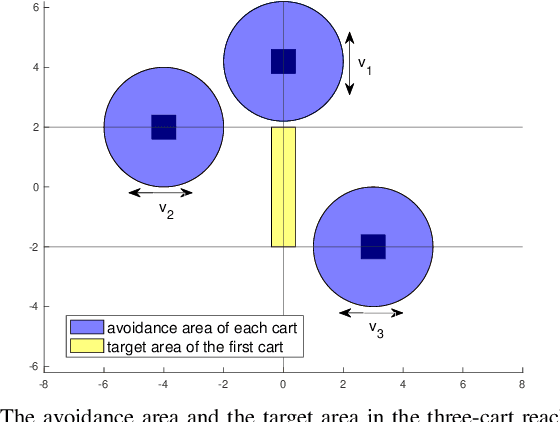
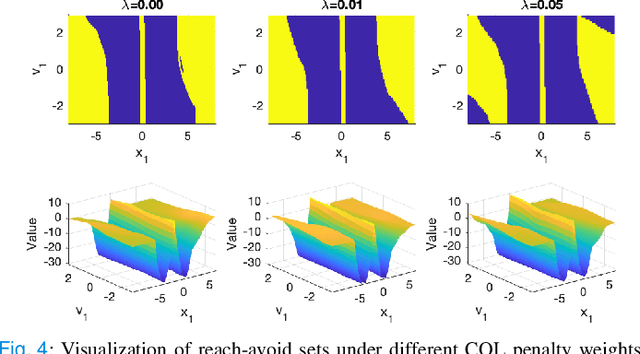
In this paper, we consider the infinite-horizon reach-avoid zero-sum game problem, where the goal is to find a set in the state space, referred to as the reach-avoid set, such that the system starting at a state therein could be controlled to reach a given target set without violating constraints under the worst-case disturbance. We address this problem by designing a new value function with a contracting Bellman backup, where the super-zero level set, i.e., the set of states where the value function is evaluated to be non-negative, recovers the reach-avoid set. Building upon this, we prove that the proposed method can be adapted to compute the viability kernel, or the set of states which could be controlled to satisfy given constraints, and the backward reachable set, or the set of states that could be driven towards a given target set. Finally, we propose to alleviate the curse of dimensionality issue in high-dimensional problems by extending Conservative Q-Learning, a deep reinforcement learning technique, to learn a value function such that the super-zero level set of the learned value function serves as a (conservative) approximation to the reach-avoid set. Our theoretical and empirical results suggest that the proposed method could learn reliably the reach-avoid set and the optimal control policy even with neural network approximation.

Partition-Based Convex Relaxations for Certifying the Robustness of ReLU Neural Networks

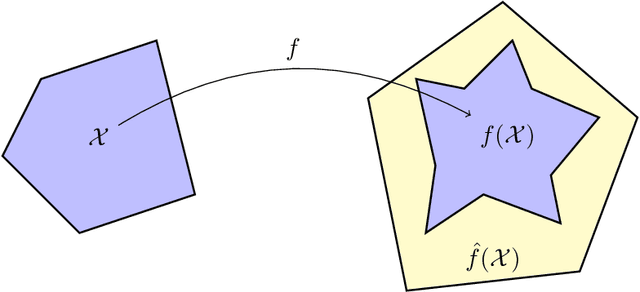
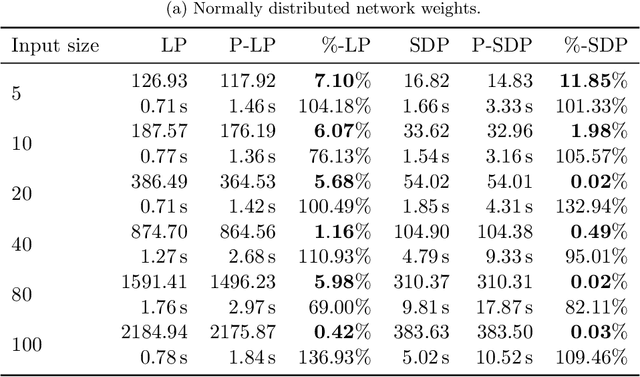
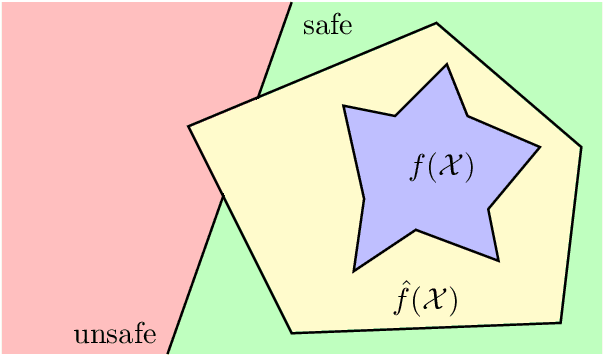
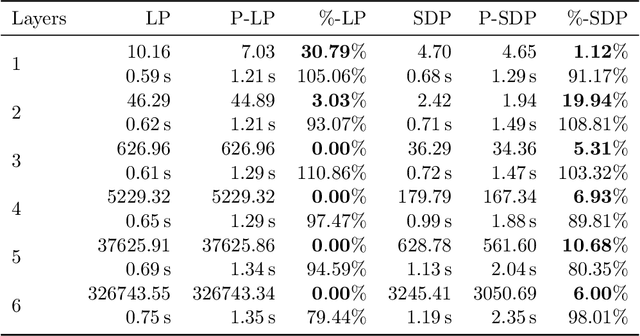
In this paper, we study certifying the robustness of ReLU neural networks against adversarial input perturbations. To diminish the relaxation error suffered by the popular linear programming (LP) and semidefinite programming (SDP) certification methods, we propose partitioning the input uncertainty set and solving the relaxations on each part separately. We show that this approach reduces relaxation error, and that the error is eliminated entirely upon performing an LP relaxation with an intelligently designed partition. To scale this approach to large networks, we consider courser partitions that take the same form as this motivating partition. We prove that computing such a partition that directly minimizes the LP relaxation error is NP-hard. By instead minimizing the worst-case LP relaxation error, we develop a computationally tractable scheme with a closed-form optimal two-part partition. We extend the analysis to the SDP, where the feasible set geometry is exploited to design a two-part partition that minimizes the worst-case SDP relaxation error. Experiments on IRIS classifiers demonstrate significant reduction in relaxation error, offering certificates that are otherwise void without partitioning. By independently increasing the input size and the number of layers, we empirically illustrate under which regimes the partitioned LP and SDP are best applied.

Tightened Convex Relaxations for Neural Network Robustness Certification

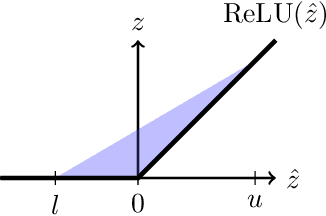
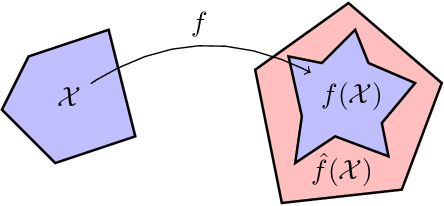
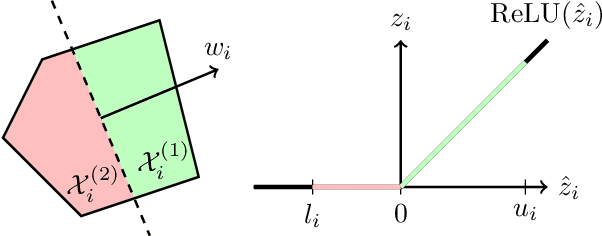
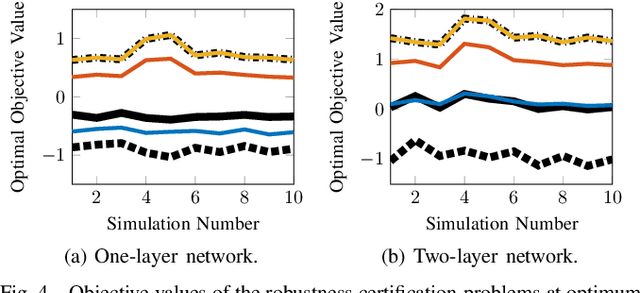
In this paper, we consider the problem of certifying the robustness of neural networks to perturbed and adversarial input data. Such certification is imperative for the application of neural networks in safety-critical decision-making and control systems. Certification techniques using convex optimization have been proposed, but they often suffer from relaxation errors that void the certificate. Our work exploits the structure of ReLU networks to improve relaxation errors through a novel partition-based certification procedure. The proposed method is proven to tighten existing linear programming relaxations, and asymptotically achieves zero relaxation error as the partition is made finer. We develop a finite partition that attains zero relaxation error and use the result to derive a tractable partitioning scheme that minimizes the worst-case relaxation error. Experiments using real data show that the partitioning procedure is able to issue robustness certificates in cases where prior methods fail. Consequently, partition-based certification procedures are found to provide an intuitive, effective, and theoretically justified method for tightening existing convex relaxation techniques.