Transport of Algebraic Structure to Latent Embeddings

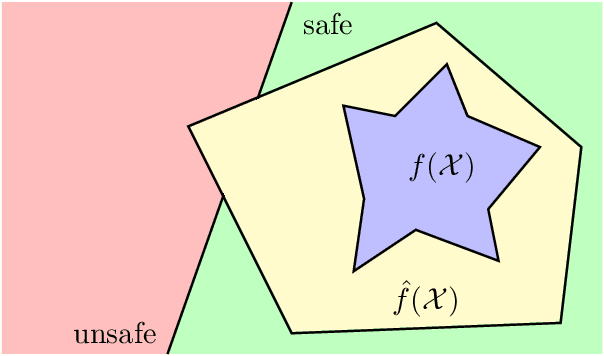
Machine learning often aims to produce latent embeddings of inputs which lie in a larger, abstract mathematical space. For example, in the field of 3D modeling, subsets of Euclidean space can be embedded as vectors using implicit neural representations. Such subsets also have a natural algebraic structure including operations (e.g., union) and corresponding laws (e.g., associativity). How can we learn to "union" two sets using only their latent embeddings while respecting associativity? We propose a general procedure for parameterizing latent space operations that are provably consistent with the laws on the input space. This is achieved by learning a bijection from the latent space to a carefully designed mirrored algebra which is constructed on Euclidean space in accordance with desired laws. We evaluate these structural transport nets for a range of mirrored algebras against baselines that operate directly on the latent space. Our experiments provide strong evidence that respecting the underlying algebraic structure of the input space is key for learning accurate and self-consistent operations.

Mixing Classifiers to Alleviate the Accuracy-Robustness Trade-Off

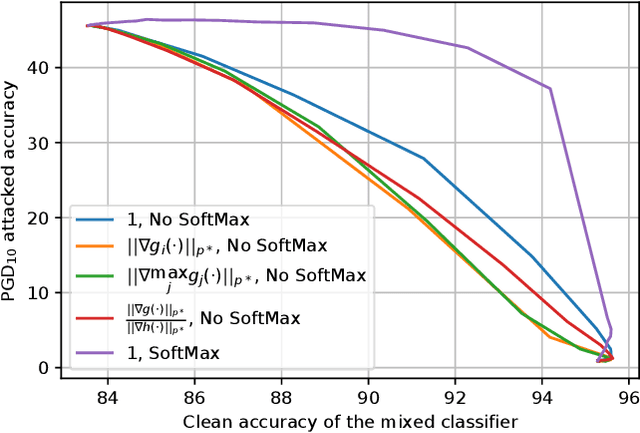
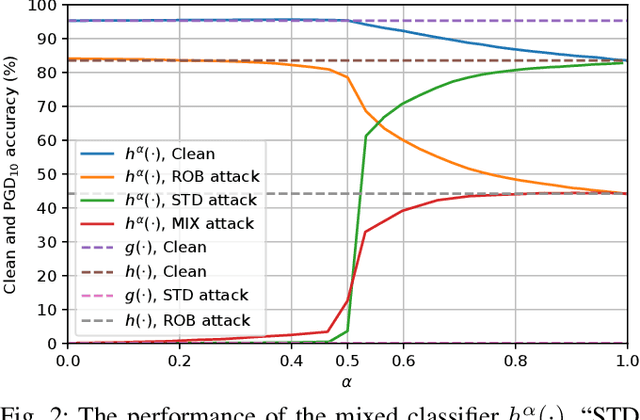
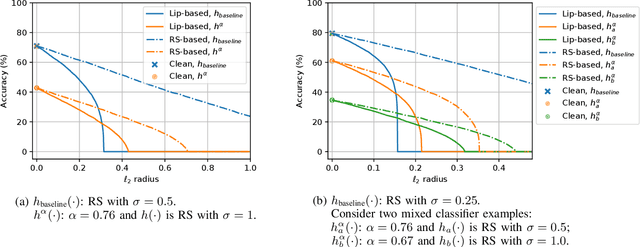
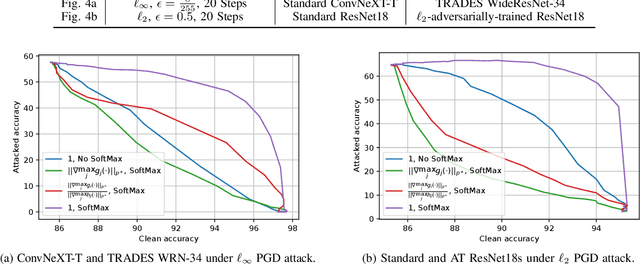
Machine learning models have recently found tremendous success in data-driven control systems. However, standard learning models often suffer from an accuracy-robustness trade-off, which is a limitation that must be overcome in the control of safety-critical systems that require both high performance and rigorous robustness guarantees. In this work, we build upon the recent "locally biased smoothing" method to develop classifiers that simultaneously inherit high accuracy from standard models and high robustness from robust models. Specifically, we extend locally biased smoothing to the multi-class setting, and then overcome its performance bottleneck by generalizing the formulation to "mix" the outputs of a standard neural network and a robust neural network. We prove that when the robustness of the robust base model is certifiable, within a closed-form $\ell_p$ radius, no alteration or attack on an input can result in misclassification of the mixed classifier; the proposed model inherits the certified robustness. Moreover, we use numerical experiments on the CIFAR-10 benchmark dataset to verify that the mixed model noticeably improves the accuracy-robustness trade-off.

Tight Certified Robustness via Min-Max Representations of ReLU Neural Networks

The reliable deployment of neural networks in control systems requires rigorous robustness guarantees. In this paper, we obtain tight robustness certificates over convex attack sets for min-max representations of ReLU neural networks by developing a convex reformulation of the nonconvex certification problem. This is done by "lifting" the problem to an infinite-dimensional optimization over probability measures, leveraging recent results in distributionally robust optimization to solve for an optimal discrete distribution, and proving that solutions of the original nonconvex problem are generated by the discrete distribution under mild boundedness, nonredundancy, and Slater conditions. As a consequence, optimal (worst-case) attacks against the model may be solved for exactly. This contrasts prior state-of-the-art that either requires expensive branch-and-bound schemes or loose relaxation techniques. Experiments on robust control and MNIST image classification examples highlight the benefits of our approach.

Projected Randomized Smoothing for Certified Adversarial Robustness

Randomized smoothing is the current state-of-the-art method for producing provably robust classifiers. While randomized smoothing typically yields robust $\ell_2$-ball certificates, recent research has generalized provable robustness to different norm balls as well as anisotropic regions. This work considers a classifier architecture that first projects onto a low-dimensional approximation of the data manifold and then applies a standard classifier. By performing randomized smoothing in the low-dimensional projected space, we characterize the certified region of our smoothed composite classifier back in the high-dimensional input space and prove a tractable lower bound on its volume. We show experimentally on CIFAR-10 and SVHN that classifiers without the initial projection are vulnerable to perturbations that are normal to the data manifold and yet are captured by the certified regions of our method. We compare the volume of our certified regions against various baselines and show that our method improves on the state-of-the-art by many orders of magnitude.

Asymmetric Certified Robustness via Feature-Convex Neural Networks

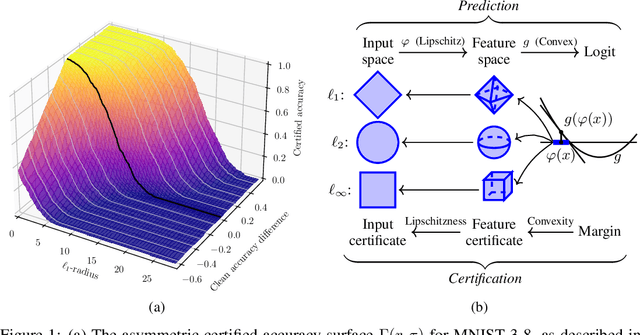
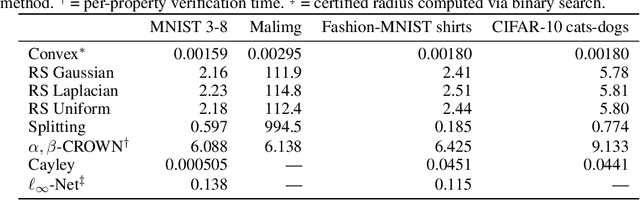
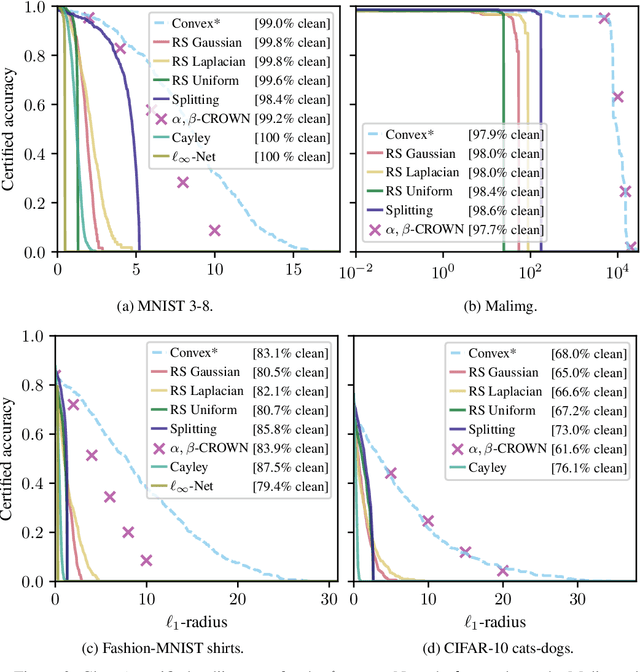
Recent works have introduced input-convex neural networks (ICNNs) as learning models with advantageous training, inference, and generalization properties linked to their convex structure. In this paper, we propose a novel feature-convex neural network architecture as the composition of an ICNN with a Lipschitz feature map in order to achieve adversarial robustness. We consider the asymmetric binary classification setting with one "sensitive" class, and for this class we prove deterministic, closed-form, and easily-computable certified robust radii for arbitrary $\ell_p$-norms. We theoretically justify the use of these models by characterizing their decision region geometry, extending the universal approximation theorem for ICNN regression to the classification setting, and proving a lower bound on the probability that such models perfectly fit even unstructured uniformly distributed data in sufficiently high dimensions. Experiments on Malimg malware classification and subsets of MNIST, Fashion-MNIST, and CIFAR-10 datasets show that feature-convex classifiers attain state-of-the-art certified $\ell_1$-radii as well as substantial $\ell_2$- and $\ell_{\infty}$-radii while being far more computationally efficient than any competitive baseline.

Improving the Accuracy-Robustness Trade-off of Classifiers via Adaptive Smoothing

While it is shown in the literature that simultaneously accurate and robust classifiers exist for common datasets, previous methods that improve the adversarial robustness of classifiers often manifest an accuracy-robustness trade-off. We build upon recent advancements in data-driven ``locally biased smoothing'' to develop classifiers that treat benign and adversarial test data differently. Specifically, we tailor the smoothing operation to the usage of a robust neural network as the source of robustness. We then extend the smoothing procedure to the multi-class setting and adapt an adversarial input detector into a policy network. The policy adaptively adjusts the mixture of the robust base classifier and a standard network, where the standard network is optimized for clean accuracy and is not robust in general. We provide theoretical analyses to motivate the use of the adaptive smoothing procedure, certify the robustness of the smoothed classifier under realistic assumptions, and justify the introduction of the policy network. We use various attack methods, including AutoAttack and adaptive attack, to empirically verify that the smoothed model noticeably improves the accuracy-robustness trade-off. On the CIFAR-100 dataset, our method simultaneously achieves an 80.09\% clean accuracy and a 32.94\% AutoAttacked accuracy. The code that implements adaptive smoothing is available at https://github.com/Bai-YT/AdaptiveSmoothing.

An Overview and Prospective Outlook on Robust Training and Certification of Machine Learning Models

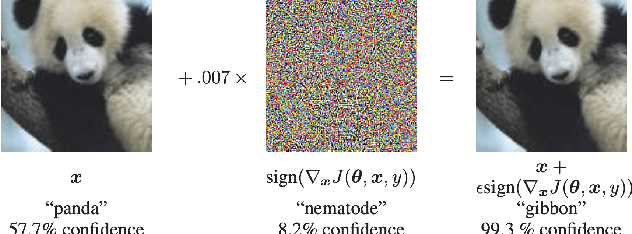
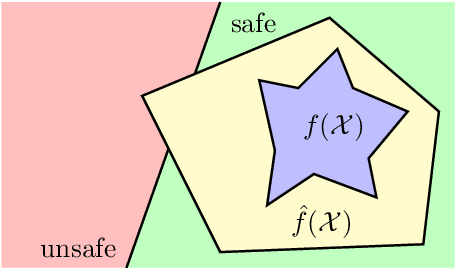
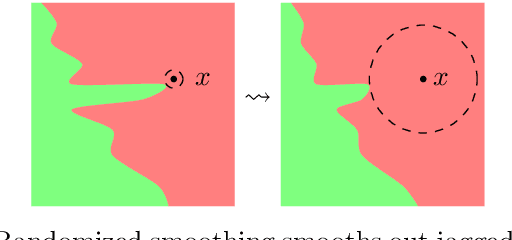
In this discussion paper, we survey recent research surrounding robustness of machine learning models. As learning algorithms become increasingly more popular in data-driven control systems, their robustness to data uncertainty must be ensured in order to maintain reliable safety-critical operations. We begin by reviewing common formalisms for such robustness, and then move on to discuss popular and state-of-the-art techniques for training robust machine learning models as well as methods for provably certifying such robustness. From this unification of robust machine learning, we identify and discuss pressing directions for future research in the area.

Node-Variant Graph Filters in Graph Neural Networks

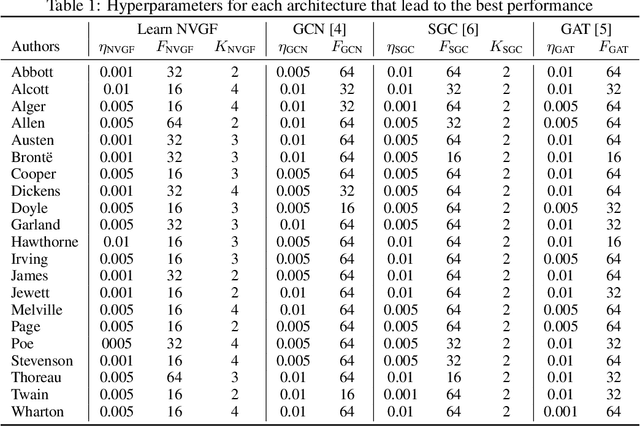
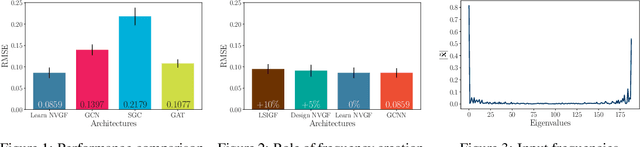
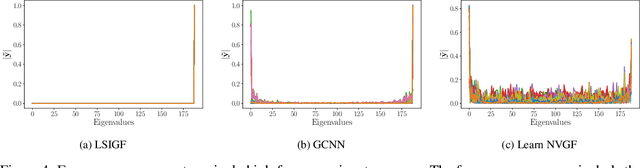
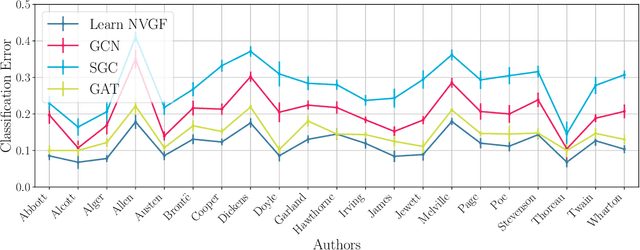
Graph neural networks (GNNs) have been successfully employed in a myriad of applications involving graph-structured data. Theoretical findings establish that GNNs use nonlinear activation functions to create low-eigenvalue frequency content that can be processed in a stable manner by subsequent graph convolutional filters. However, the exact shape of the frequency content created by nonlinear functions is not known, and thus, it cannot be learned nor controlled. In this work, node-variant graph filters (NVGFs) are shown to be capable of creating frequency content and are thus used in lieu of nonlinear activation functions. This results in a novel GNN architecture that, although linear, is capable of creating frequency content as well. Furthermore, this new frequency content can be either designed or learned from data. In this way, the role of frequency creation is separated from the nonlinear nature of traditional GNNs. Extensive simulations are carried out to differentiate the contributions of frequency creation from those of the nonlinearity.

Partition-Based Convex Relaxations for Certifying the Robustness of ReLU Neural Networks

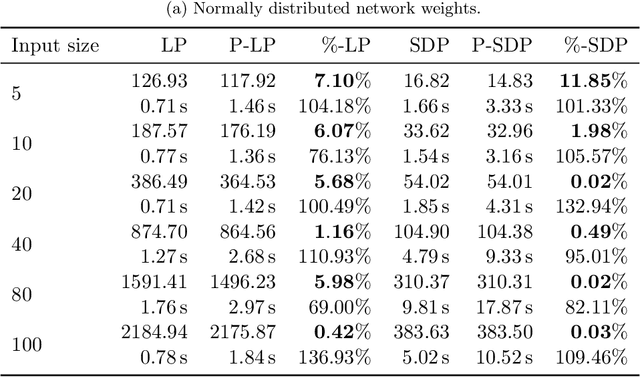
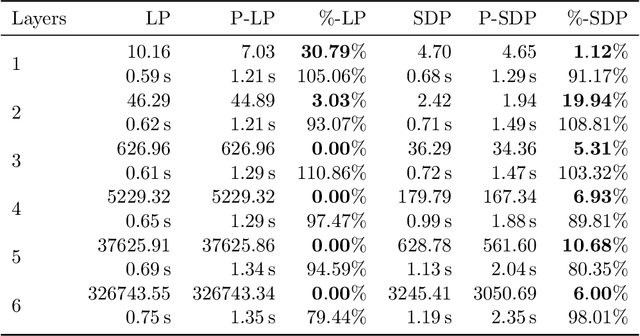
In this paper, we study certifying the robustness of ReLU neural networks against adversarial input perturbations. To diminish the relaxation error suffered by the popular linear programming (LP) and semidefinite programming (SDP) certification methods, we propose partitioning the input uncertainty set and solving the relaxations on each part separately. We show that this approach reduces relaxation error, and that the error is eliminated entirely upon performing an LP relaxation with an intelligently designed partition. To scale this approach to large networks, we consider courser partitions that take the same form as this motivating partition. We prove that computing such a partition that directly minimizes the LP relaxation error is NP-hard. By instead minimizing the worst-case LP relaxation error, we develop a computationally tractable scheme with a closed-form optimal two-part partition. We extend the analysis to the SDP, where the feasible set geometry is exploited to design a two-part partition that minimizes the worst-case SDP relaxation error. Experiments on IRIS classifiers demonstrate significant reduction in relaxation error, offering certificates that are otherwise void without partitioning. By independently increasing the input size and the number of layers, we empirically illustrate under which regimes the partitioned LP and SDP are best applied.

Certifying Neural Network Robustness to Random Input Noise from Samples

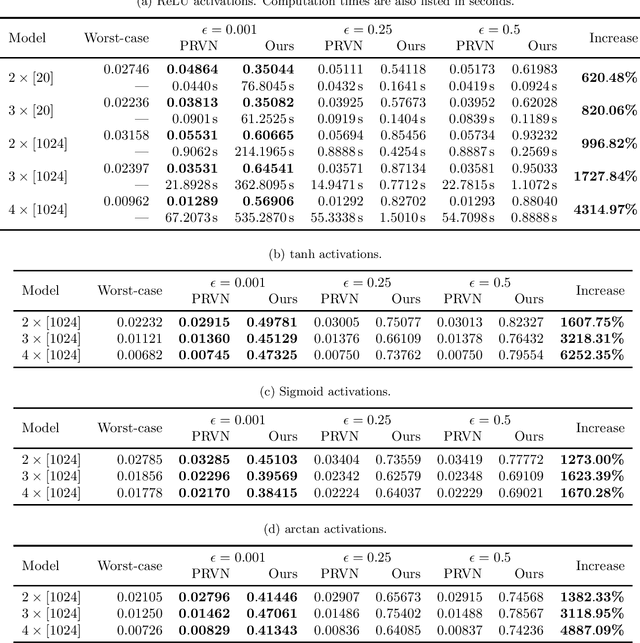
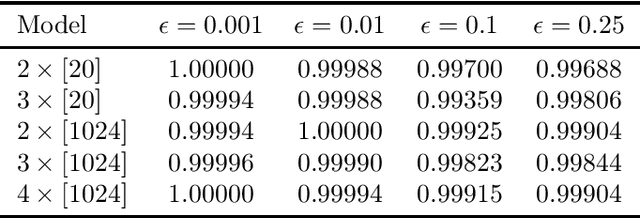
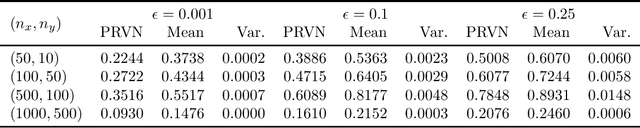
Methods to certify the robustness of neural networks in the presence of input uncertainty are vital in safety-critical settings. Most certification methods in the literature are designed for adversarial input uncertainty, but researchers have recently shown a need for methods that consider random uncertainty. In this paper, we propose a novel robustness certification method that upper bounds the probability of misclassification when the input noise follows an arbitrary probability distribution. This bound is cast as a chance-constrained optimization problem, which is then reformulated using input-output samples to replace the optimization constraints. The resulting optimization reduces to a linear program with an analytical solution. Furthermore, we develop a sufficient condition on the number of samples needed to make the misclassification bound hold with overwhelming probability. Our case studies on MNIST classifiers show that this method is able to certify a uniform infinity-norm uncertainty region with a radius of nearly 50 times larger than what the current state-of-the-art method can certify.