Asymmetric Certified Robustness via Feature-Convex Neural Networks
Paper and Code
Feb 03, 2023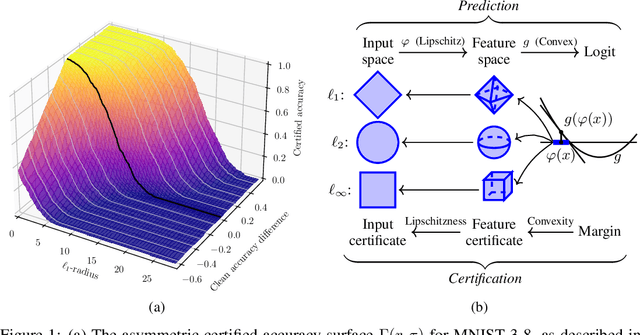
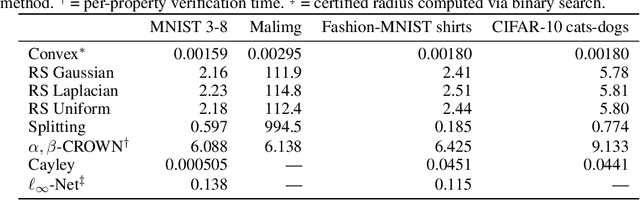
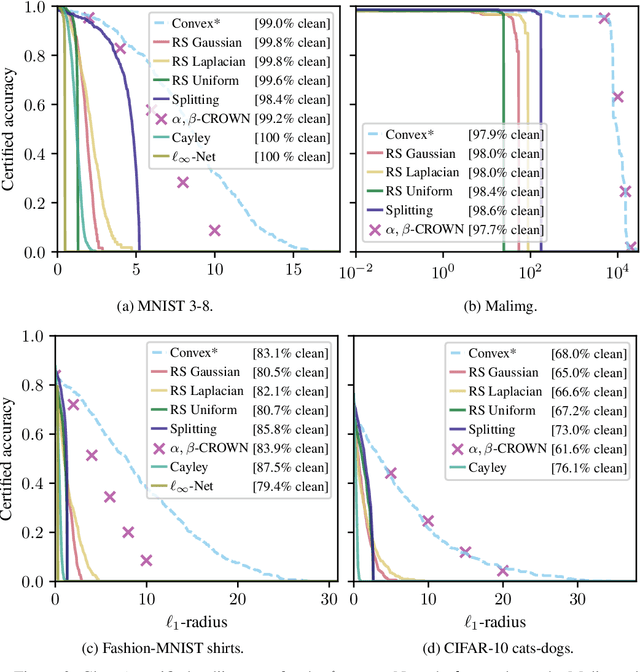

Recent works have introduced input-convex neural networks (ICNNs) as learning models with advantageous training, inference, and generalization properties linked to their convex structure. In this paper, we propose a novel feature-convex neural network architecture as the composition of an ICNN with a Lipschitz feature map in order to achieve adversarial robustness. We consider the asymmetric binary classification setting with one "sensitive" class, and for this class we prove deterministic, closed-form, and easily-computable certified robust radii for arbitrary $\ell_p$-norms. We theoretically justify the use of these models by characterizing their decision region geometry, extending the universal approximation theorem for ICNN regression to the classification setting, and proving a lower bound on the probability that such models perfectly fit even unstructured uniformly distributed data in sufficiently high dimensions. Experiments on Malimg malware classification and subsets of MNIST, Fashion-MNIST, and CIFAR-10 datasets show that feature-convex classifiers attain state-of-the-art certified $\ell_1$-radii as well as substantial $\ell_2$- and $\ell_{\infty}$-radii while being far more computationally efficient than any competitive baseline.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge