Certifying Neural Network Robustness to Random Input Noise from Samples

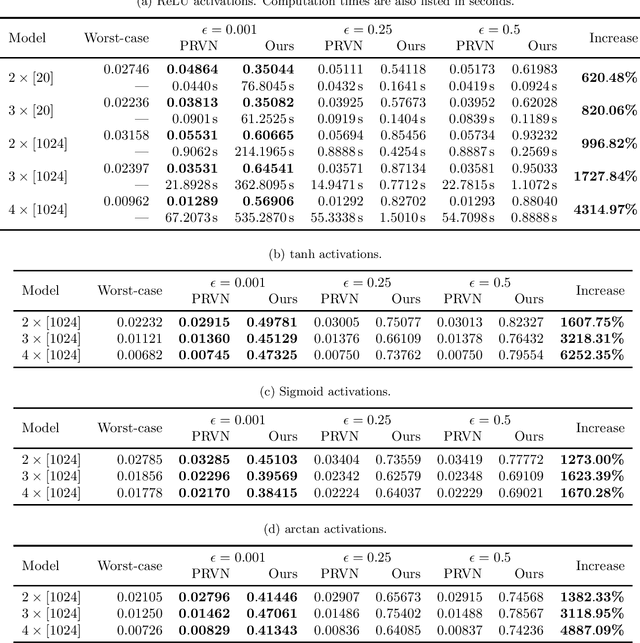
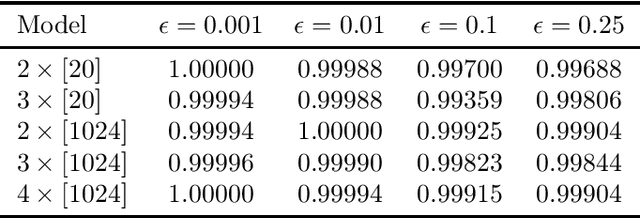
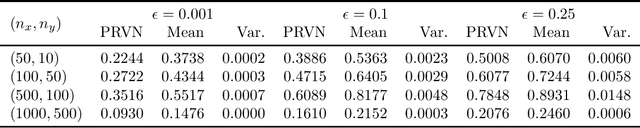
Methods to certify the robustness of neural networks in the presence of input uncertainty are vital in safety-critical settings. Most certification methods in the literature are designed for adversarial input uncertainty, but researchers have recently shown a need for methods that consider random uncertainty. In this paper, we propose a novel robustness certification method that upper bounds the probability of misclassification when the input noise follows an arbitrary probability distribution. This bound is cast as a chance-constrained optimization problem, which is then reformulated using input-output samples to replace the optimization constraints. The resulting optimization reduces to a linear program with an analytical solution. Furthermore, we develop a sufficient condition on the number of samples needed to make the misclassification bound hold with overwhelming probability. Our case studies on MNIST classifiers show that this method is able to certify a uniform infinity-norm uncertainty region with a radius of nearly 50 times larger than what the current state-of-the-art method can certify.