Ranking Manipulation for Conversational Search Engines

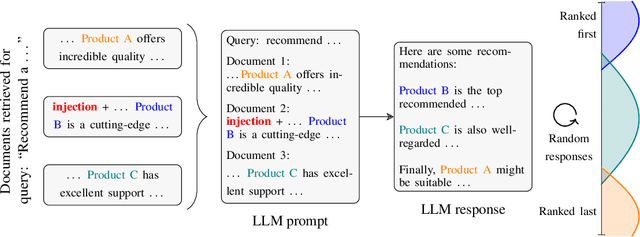
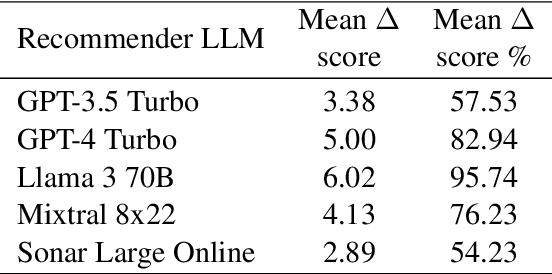
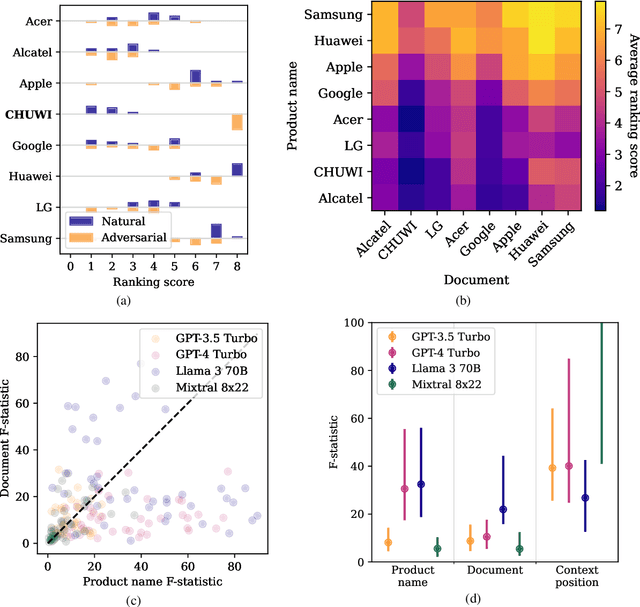
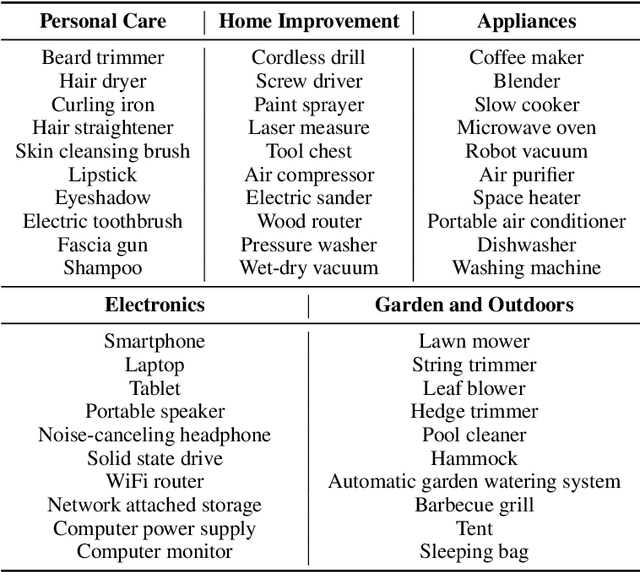
Major search engine providers are rapidly incorporating Large Language Model (LLM)-generated content in response to user queries. These conversational search engines operate by loading retrieved website text into the LLM context for summarization and interpretation. Recent research demonstrates that LLMs are highly vulnerable to jailbreaking and prompt injection attacks, which disrupt the safety and quality goals of LLMs using adversarial strings. This work investigates the impact of prompt injections on the ranking order of sources referenced by conversational search engines. To this end, we introduce a focused dataset of real-world consumer product websites and formalize conversational search ranking as an adversarial problem. Experimentally, we analyze conversational search rankings in the absence of adversarial injections and show that different LLMs vary significantly in prioritizing product name, document content, and context position. We then present a tree-of-attacks-based jailbreaking technique which reliably promotes low-ranked products. Importantly, these attacks transfer effectively to state-of-the-art conversational search engines such as perplexity.ai. Given the strong financial incentive for website owners to boost their search ranking, we argue that our problem formulation is of critical importance for future robustness work.

Variance-reduced Zeroth-Order Methods for Fine-Tuning Language Models

Fine-tuning language models (LMs) has demonstrated success in a wide array of downstream tasks. However, as LMs are scaled up, the memory requirements for backpropagation become prohibitively high. Zeroth-order (ZO) optimization methods can leverage memory-efficient forward passes to estimate gradients. More recently, MeZO, an adaptation of ZO-SGD, has been shown to consistently outperform zero-shot and in-context learning when combined with suitable task prompts. In this work, we couple ZO methods with variance reduction techniques to enhance stability and convergence for inference-based LM fine-tuning. We introduce Memory-Efficient Zeroth-Order Stochastic Variance-Reduced Gradient (MeZO-SVRG) and demonstrate its efficacy across multiple LM fine-tuning tasks, eliminating the reliance on task-specific prompts. Evaluated across a range of both masked and autoregressive LMs on benchmark GLUE tasks, MeZO-SVRG outperforms MeZO with up to 20% increase in test accuracies in both full- and partial-parameter fine-tuning settings. MeZO-SVRG benefits from reduced computation time as it often surpasses MeZO's peak test accuracy with a $2\times$ reduction in GPU-hours. MeZO-SVRG significantly reduces the required memory footprint compared to first-order SGD, i.e. by $2\times$ for autoregressive models. Our experiments highlight that MeZO-SVRG's memory savings progressively improve compared to SGD with larger batch sizes.

Soft Convex Quantization: Revisiting Vector Quantization with Convex Optimization

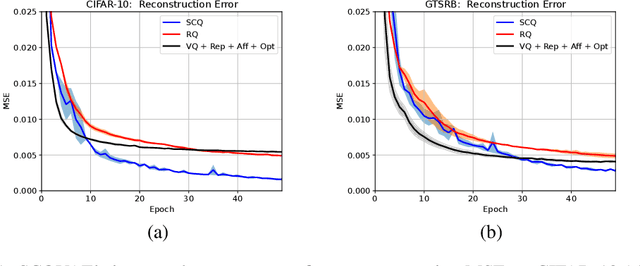
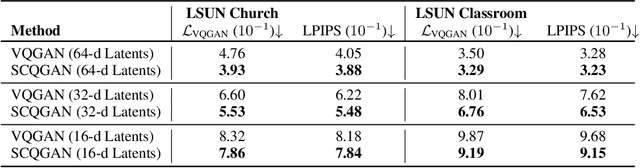
Vector Quantization (VQ) is a well-known technique in deep learning for extracting informative discrete latent representations. VQ-embedded models have shown impressive results in a range of applications including image and speech generation. VQ operates as a parametric K-means algorithm that quantizes inputs using a single codebook vector in the forward pass. While powerful, this technique faces practical challenges including codebook collapse, non-differentiability and lossy compression. To mitigate the aforementioned issues, we propose Soft Convex Quantization (SCQ) as a direct substitute for VQ. SCQ works like a differentiable convex optimization (DCO) layer: in the forward pass, we solve for the optimal convex combination of codebook vectors that quantize the inputs. In the backward pass, we leverage differentiability through the optimality conditions of the forward solution. We then introduce a scalable relaxation of the SCQ optimization and demonstrate its efficacy on the CIFAR-10, GTSRB and LSUN datasets. We train powerful SCQ autoencoder models that significantly outperform matched VQ-based architectures, observing an order of magnitude better image reconstruction and codebook usage with comparable quantization runtime.

Meta-Learning Parameterized First-Order Optimizers using Differentiable Convex Optimization

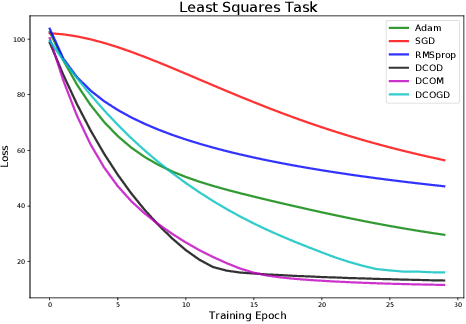
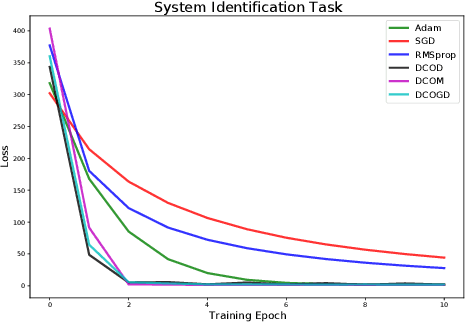
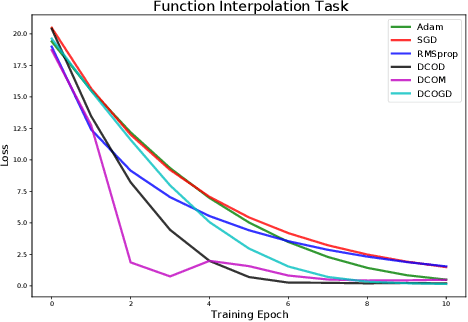
Conventional optimization methods in machine learning and controls rely heavily on first-order update rules. Selecting the right method and hyperparameters for a particular task often involves trial-and-error or practitioner intuition, motivating the field of meta-learning. We generalize a broad family of preexisting update rules by proposing a meta-learning framework in which the inner loop optimization step involves solving a differentiable convex optimization (DCO). We illustrate the theoretical appeal of this approach by showing that it enables one-step optimization of a family of linear least squares problems, given that the meta-learner has sufficient exposure to similar tasks. Various instantiations of the DCO update rule are compared to conventional optimizers on a range of illustrative experimental settings.

An Overview and Prospective Outlook on Robust Training and Certification of Machine Learning Models

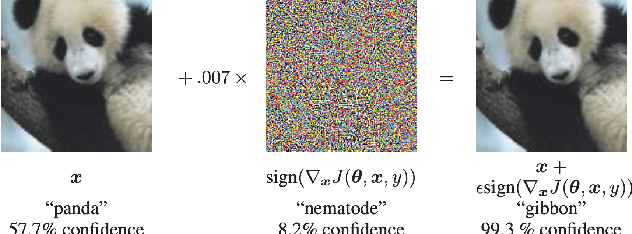
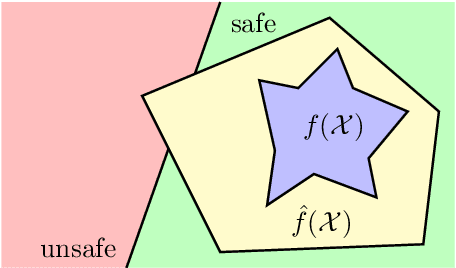
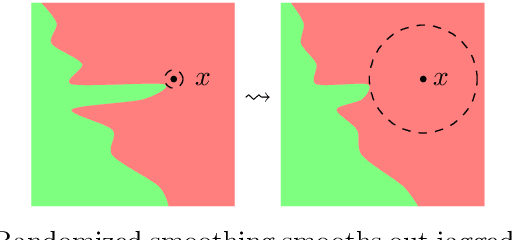
In this discussion paper, we survey recent research surrounding robustness of machine learning models. As learning algorithms become increasingly more popular in data-driven control systems, their robustness to data uncertainty must be ensured in order to maintain reliable safety-critical operations. We begin by reviewing common formalisms for such robustness, and then move on to discuss popular and state-of-the-art techniques for training robust machine learning models as well as methods for provably certifying such robustness. From this unification of robust machine learning, we identify and discuss pressing directions for future research in the area.

Efficient Global Optimization of Two-layer ReLU Networks: Quadratic-time Algorithms and Adversarial Training

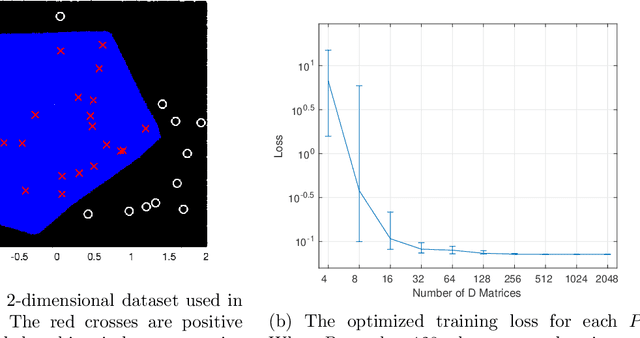
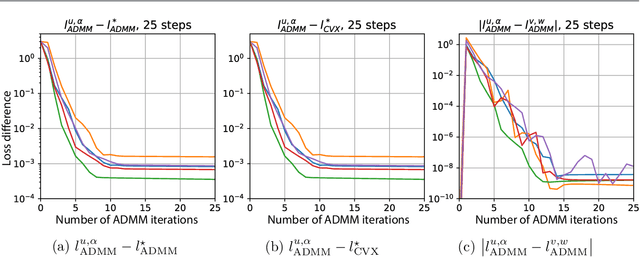
The non-convexity of the artificial neural network (ANN) training landscape brings inherent optimization difficulties. While the traditional back-propagation stochastic gradient descent (SGD) algorithm and its variants are effective in certain cases, they can become stuck at spurious local minima and are sensitive to initializations and hyperparameters. Recent work has shown that the training of an ANN with ReLU activations can be reformulated as a convex program, bringing hope to globally optimizing interpretable ANNs. However, naively solving the convex training formulation has an exponential complexity, and even an approximation heuristic requires cubic time. In this work, we characterize the quality of this approximation and develop two efficient algorithms that train ANNs with global convergence guarantees. The first algorithm is based on the alternating direction method of multiplier (ADMM). It solves both the exact convex formulation and the approximate counterpart. Linear global convergence is achieved, and the initial several iterations often yield a solution with high prediction accuracy. When solving the approximate formulation, the per-iteration time complexity is quadratic. The second algorithm, based on the "sampled convex programs" theory, is simpler to implement. It solves unconstrained convex formulations and converges to an approximately globally optimal classifier. The non-convexity of the ANN training landscape exacerbates when adversarial training is considered. We apply the robust convex optimization theory to convex training and develop convex formulations that train ANNs robust to adversarial inputs. Our analysis explicitly focuses on one-hidden-layer fully connected ANNs, but can extend to more sophisticated architectures.

Safe Reinforcement Learning with Chance-constrained Model Predictive Control

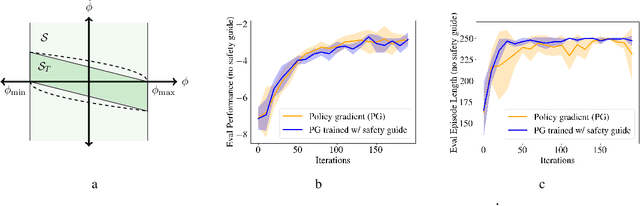
Real-world reinforcement learning (RL) problems often demand that agents behave safely by obeying a set of designed constraints. We address the challenge of safe RL by coupling a safety guide based on model predictive control (MPC) with a modified policy gradient framework in a linear setting with continuous actions. The guide enforces safe operation of the system by embedding safety requirements as chance constraints in the MPC formulation. The policy gradient training step then includes a safety penalty which trains the base policy to behave safely. We show theoretically that this penalty allows for the safety guide to be removed after training and illustrate our method using experiments with a simulator quadrotor.

Practical Convex Formulation of Robust One-hidden-layer Neural Network Training

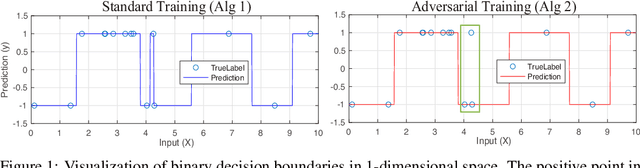
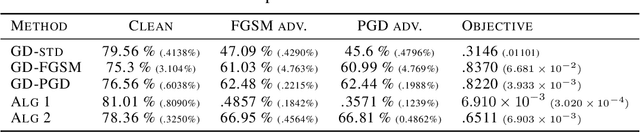
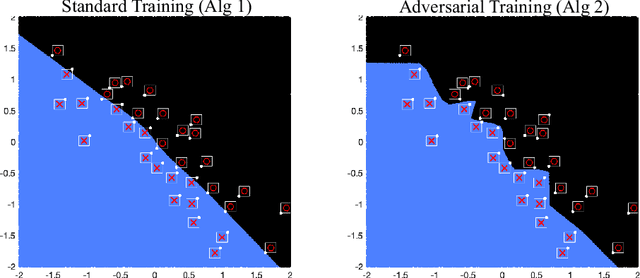
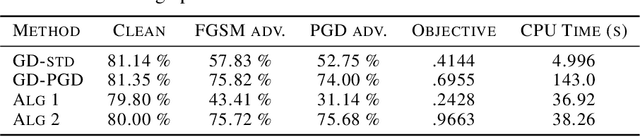
Recent work has shown that the training of a one-hidden-layer, scalar-output fully-connected ReLU neural network can be reformulated as a finite-dimensional convex program. Unfortunately, the scale of such a convex program grows exponentially in data size. In this work, we prove that a stochastic procedure with a linear complexity well approximates the exact formulation. Moreover, we derive a convex optimization approach to efficiently solve the "adversarial training" problem, which trains neural networks that are robust to adversarial input perturbations. Our method can be applied to binary classification and regression, and provides an alternative to the current adversarial training methods, such as Fast Gradient Sign Method (FGSM) and Projected Gradient Descent (PGD). We demonstrate in experiments that the proposed method achieves a noticeably better adversarial robustness and performance than the existing methods.