Adaptive Batch Sizes Using Non-Euclidean Gradient Noise Scales for Stochastic Sign and Spectral Descent

To maximize hardware utilization, modern machine learning systems typically employ large constant or manually tuned batch size schedules, relying on heuristics that are brittle and costly to tune. Existing adaptive strategies based on gradient noise scale (GNS) offer a principled alternative. However, their assumption of SGD's Euclidean geometry creates a fundamental mismatch with popular optimizers based on generalized norms, such as signSGD / Signum ($\ell_\infty$) and stochastic spectral descent (specSGD) / Muon ($\mathcal{S}_\infty$). In this work, we derive gradient noise scales for signSGD and specSGD that naturally emerge from the geometry of their respective dual norms. To practically estimate these non-Euclidean metrics, we propose an efficient variance estimation procedure that leverages the local mini-batch gradients on different ranks in distributed data-parallel systems. Our experiments demonstrate that adaptive batch size strategies using non-Euclidean GNS enable us to match the validation loss of constant-batch baselines while reducing training steps by up to 66% for Signum and Muon on a 160 million parameter Llama model.

Smoothing DiLoCo with Primal Averaging for Faster Training of LLMs

We propose Generalized Primal Averaging (GPA), an extension of Nesterov's method in its primal averaging formulation that addresses key limitations of recent averaging-based optimizers such as single-worker DiLoCo and Schedule-Free (SF) in the non-distributed setting. These two recent algorithmic approaches improve the performance of base optimizers, such as AdamW, through different iterate averaging strategies. Schedule-Free explicitly maintains a uniform average of past weights, while single-worker DiLoCo performs implicit averaging by periodically aggregating trajectories, called pseudo-gradients, to update the model parameters. However, single-worker DiLoCo's periodic averaging introduces a two-loop structure, increasing its memory requirements and number of hyperparameters. GPA overcomes these limitations by decoupling the interpolation constant in the primal averaging formulation of Nesterov. This decoupling enables GPA to smoothly average iterates at every step, generalizing and improving upon single-worker DiLoCo. Empirically, GPA consistently outperforms single-worker DiLoCo while removing the two-loop structure, simplifying hyperparameter tuning, and reducing its memory overhead to a single additional buffer. On the Llama-160M model, GPA provides a 24.22% speedup in terms of steps to reach the baseline (AdamW's) validation loss. Likewise, GPA achieves speedups of 12% and 27% on small and large batch setups, respectively, to attain AdamW's validation accuracy on the ImageNet ViT workload. Furthermore, we prove that for any base optimizer with regret bounded by $O(\sqrt{T})$, where $T$ is the number of iterations, GPA can match or exceed the convergence guarantee of the original optimizer, depending on the choice of interpolation constants.

HLAT: High-quality Large Language Model Pre-trained on AWS Trainium

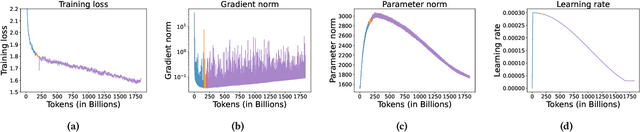
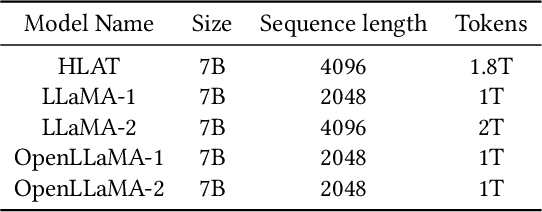
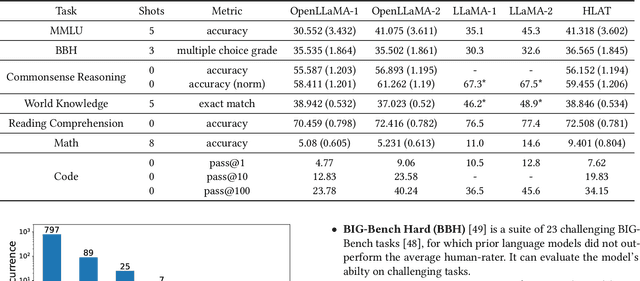
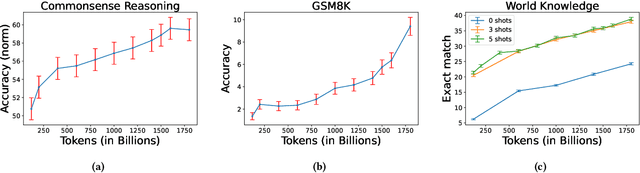
Getting large language models (LLMs) to perform well on the downstream tasks requires pre-training over trillions of tokens. This typically demands a large number of powerful computational devices in addition to a stable distributed training framework to accelerate the training. The growing number of applications leveraging AI/ML had led to a scarcity of the expensive conventional accelerators (such as GPUs), which begs the need for the alternative specialized-accelerators that are scalable and cost-efficient. AWS Trainium is the second-generation machine learning accelerator that has been purposely built for training large deep learning models. Its corresponding instance, Amazon EC2 trn1, is an alternative to GPU instances for LLM training. However, training LLMs with billions of parameters on trn1 is challenging due to its relatively nascent software ecosystem. In this paper, we showcase HLAT: a 7 billion parameter decoder-only LLM pre-trained using trn1 instances over 1.8 trillion tokens. The performance of HLAT is benchmarked against popular open source baseline models including LLaMA and OpenLLaMA, which have been trained on NVIDIA GPUs and Google TPUs, respectively. On various evaluation tasks, we show that HLAT achieves model quality on par with the baselines. We also share the best practice of using the Neuron Distributed Training Library (NDTL), a customized distributed training library for AWS Trainium to achieve efficient training. Our work demonstrates that AWS Trainium powered by the NDTL is able to successfully pre-train state-of-the-art LLM models with high performance and cost-effectiveness.

EMC$^2$: Efficient MCMC Negative Sampling for Contrastive Learning with Global Convergence

A key challenge in contrastive learning is to generate negative samples from a large sample set to contrast with positive samples, for learning better encoding of the data. These negative samples often follow a softmax distribution which are dynamically updated during the training process. However, sampling from this distribution is non-trivial due to the high computational costs in computing the partition function. In this paper, we propose an Efficient Markov Chain Monte Carlo negative sampling method for Contrastive learning (EMC$^2$). We follow the global contrastive learning loss as introduced in SogCLR, and propose EMC$^2$ which utilizes an adaptive Metropolis-Hastings subroutine to generate hardness-aware negative samples in an online fashion during the optimization. We prove that EMC$^2$ finds an $\mathcal{O}(1/\sqrt{T})$-stationary point of the global contrastive loss in $T$ iterations. Compared to prior works, EMC$^2$ is the first algorithm that exhibits global convergence (to stationarity) regardless of the choice of batch size while exhibiting low computation and memory cost. Numerical experiments validate that EMC$^2$ is effective with small batch training and achieves comparable or better performance than baseline algorithms. We report the results for pre-training image encoders on STL-10 and Imagenet-100.

Variance-reduced Zeroth-Order Methods for Fine-Tuning Language Models

Fine-tuning language models (LMs) has demonstrated success in a wide array of downstream tasks. However, as LMs are scaled up, the memory requirements for backpropagation become prohibitively high. Zeroth-order (ZO) optimization methods can leverage memory-efficient forward passes to estimate gradients. More recently, MeZO, an adaptation of ZO-SGD, has been shown to consistently outperform zero-shot and in-context learning when combined with suitable task prompts. In this work, we couple ZO methods with variance reduction techniques to enhance stability and convergence for inference-based LM fine-tuning. We introduce Memory-Efficient Zeroth-Order Stochastic Variance-Reduced Gradient (MeZO-SVRG) and demonstrate its efficacy across multiple LM fine-tuning tasks, eliminating the reliance on task-specific prompts. Evaluated across a range of both masked and autoregressive LMs on benchmark GLUE tasks, MeZO-SVRG outperforms MeZO with up to 20% increase in test accuracies in both full- and partial-parameter fine-tuning settings. MeZO-SVRG benefits from reduced computation time as it often surpasses MeZO's peak test accuracy with a $2\times$ reduction in GPU-hours. MeZO-SVRG significantly reduces the required memory footprint compared to first-order SGD, i.e. by $2\times$ for autoregressive models. Our experiments highlight that MeZO-SVRG's memory savings progressively improve compared to SGD with larger batch sizes.

MADA: Meta-Adaptive Optimizers through hyper-gradient Descent

Since Adam was introduced, several novel adaptive optimizers for deep learning have been proposed. These optimizers typically excel in some tasks but may not outperform Adam uniformly across all tasks. In this work, we introduce Meta-Adaptive Optimizers (MADA), a unified optimizer framework that can generalize several known optimizers and dynamically learn the most suitable one during training. The key idea in MADA is to parameterize the space of optimizers and search through it using hyper-gradient descent. Numerical results suggest that MADA is robust against sub-optimally tuned hyper-parameters, and outperforms Adam, Lion, and Adan with their default hyper-parameters, often even with optimized hyper-parameters. We also propose AVGrad, a variant of AMSGrad where the maximum operator is replaced with averaging, and observe that it performs better within MADA. Finally, we provide a convergence analysis to show that interpolation of optimizers (specifically, AVGrad and Adam) can improve their error bounds (up to constants), hinting at an advantage for meta-optimizers.

Krylov Cubic Regularized Newton: A Subspace Second-Order Method with Dimension-Free Convergence Rate

Second-order optimization methods, such as cubic regularized Newton methods, are known for their rapid convergence rates; nevertheless, they become impractical in high-dimensional problems due to their substantial memory requirements and computational costs. One promising approach is to execute second-order updates within a lower-dimensional subspace, giving rise to subspace second-order methods. However, the majority of existing subspace second-order methods randomly select subspaces, consequently resulting in slower convergence rates depending on the problem's dimension $d$. In this paper, we introduce a novel subspace cubic regularized Newton method that achieves a dimension-independent global convergence rate of ${O}\left(\frac{1}{mk}+\frac{1}{k^2}\right)$ for solving convex optimization problems. Here, $m$ represents the subspace dimension, which can be significantly smaller than $d$. Instead of adopting a random subspace, our primary innovation involves performing the cubic regularized Newton update within the Krylov subspace associated with the Hessian and the gradient of the objective function. This result marks the first instance of a dimension-independent convergence rate for a subspace second-order method. Furthermore, when specific spectral conditions of the Hessian are met, our method recovers the convergence rate of a full-dimensional cubic regularized Newton method. Numerical experiments show our method converges faster than existing random subspace methods, especially for high-dimensional problems.

Contractive error feedback for gradient compression

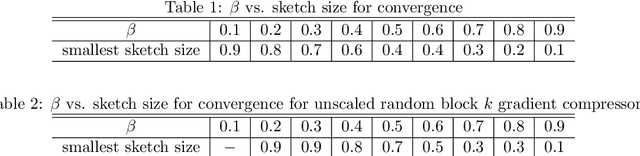
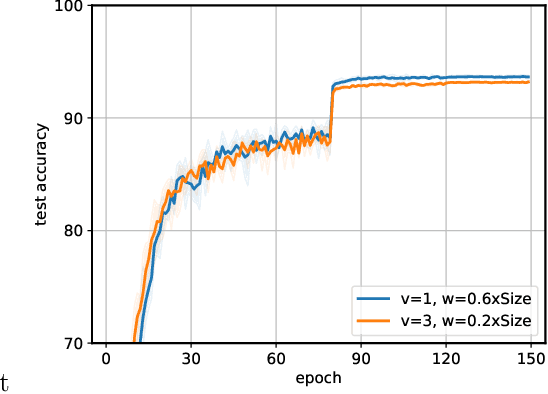
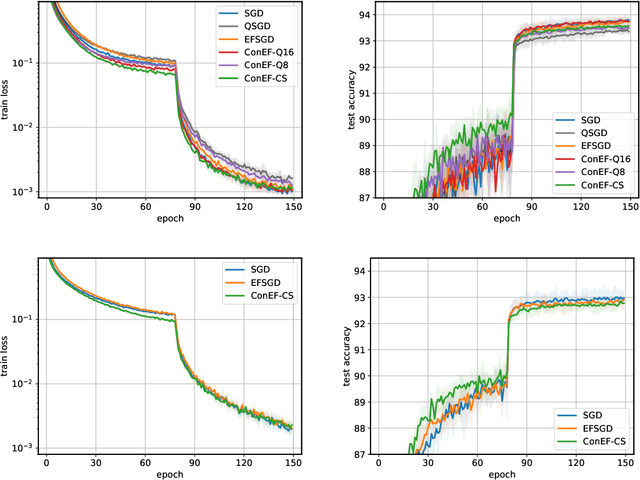
On-device memory concerns in distributed deep learning have become severe due to (i) the growth of model size in multi-GPU training, and (ii) the wide adoption of deep neural networks for federated learning on IoT devices which have limited storage. In such settings, communication efficient optimization methods are attractive alternatives, however they still struggle with memory issues. To tackle these challenges, we propose an communication efficient method called contractive error feedback (ConEF). As opposed to SGD with error-feedback (EFSGD) that inefficiently manages memory, ConEF obtains the sweet spot of convergence and memory usage, and achieves communication efficiency by leveraging biased and all-reducable gradient compression. We empirically validate ConEF on various learning tasks that include image classification, language modeling, and machine translation and observe that ConEF saves 80\% - 90\% of the extra memory in EFSGD with almost no loss on test performance, while also achieving 1.3x - 5x speedup of SGD. Through our work, we also demonstrate the feasibility and convergence of ConEF to clear up the theoretical barrier of integrating ConEF to popular memory efficient frameworks such as ZeRO-3.

DS-FACTO: Doubly Separable Factorization Machines

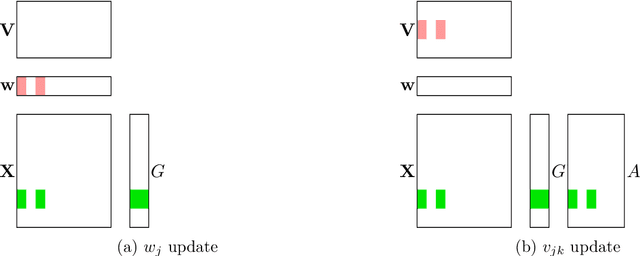
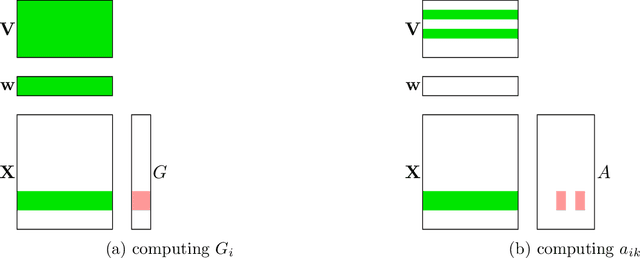
Factorization Machines (FM) are powerful class of models that incorporate higher-order interaction among features to add more expressive power to linear models. They have been used successfully in several real-world tasks such as click-prediction, ranking and recommender systems. Despite using a low-rank representation for the pairwise features, the memory overheads of using factorization machines on large-scale real-world datasets can be prohibitively high. For instance on the criteo tera dataset, assuming a modest $128$ dimensional latent representation and $10^{9}$ features, the memory requirement for the model is in the order of $1$ TB. In addition, the data itself occupies $2.1$ TB. Traditional algorithms for FM which work on a single-machine are not equipped to handle this scale and therefore, using a distributed algorithm to parallelize the computation across a cluster is inevitable. In this work, we propose a hybrid-parallel stochastic optimization algorithm DS-FACTO, which partitions both the data as well as parameters of the factorization machine simultaneously. Our solution is fully de-centralized and does not require the use of any parameter servers. We present empirical results to analyze the convergence behavior, predictive power and scalability of DS-FACTO.

Optimization on the Surface of the -Sphere

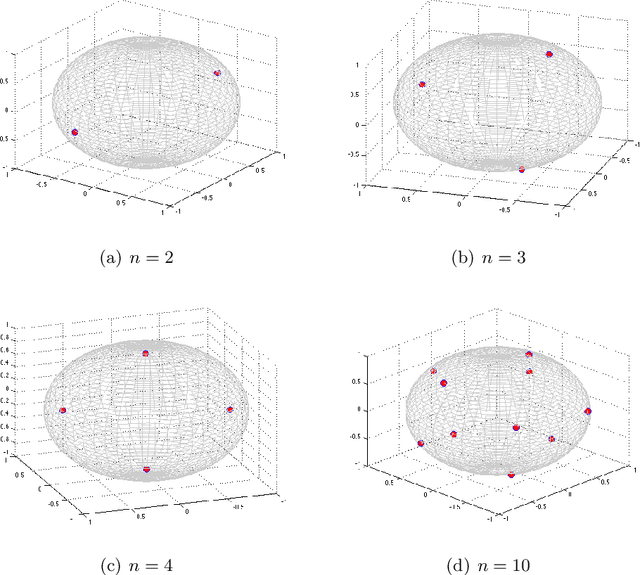
Thomson problem is a classical problem in physics to study how $n$ number of charged particles distribute themselves on the surface of a sphere of $k$ dimensions. When $k=2$, i.e. a 2-sphere (a circle), the particles appear at equally spaced points. Such a configuration can be computed analytically. However, for higher dimensions such as $k \ge 3$, i.e. the case of 3-sphere (standard sphere), there is not much that is understood analytically. Finding global minimum of the problem under these settings is particularly tough since the optimization problem becomes increasingly computationally intensive with larger values of $k$ and $n$. In this work, we explore a wide variety of numerical optimization methods to solve the Thomson problem. In our empirical study, we find stochastic gradient based methods (SGD) to be a compelling choice for this problem as it scales well with the number of points.