Optimization on the Surface of the -Sphere

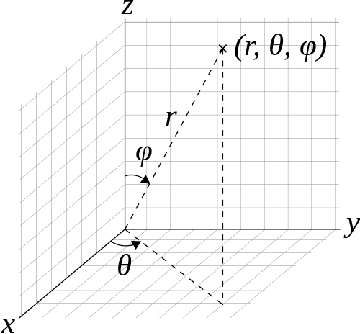
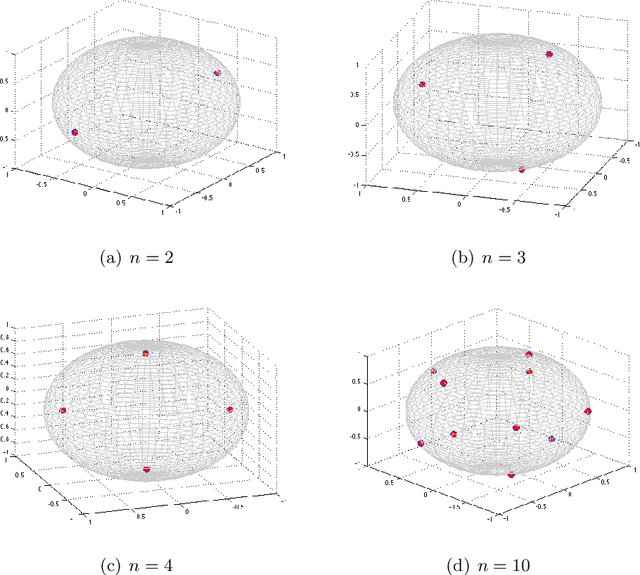
Thomson problem is a classical problem in physics to study how $n$ number of charged particles distribute themselves on the surface of a sphere of $k$ dimensions. When $k=2$, i.e. a 2-sphere (a circle), the particles appear at equally spaced points. Such a configuration can be computed analytically. However, for higher dimensions such as $k \ge 3$, i.e. the case of 3-sphere (standard sphere), there is not much that is understood analytically. Finding global minimum of the problem under these settings is particularly tough since the optimization problem becomes increasingly computationally intensive with larger values of $k$ and $n$. In this work, we explore a wide variety of numerical optimization methods to solve the Thomson problem. In our empirical study, we find stochastic gradient based methods (SGD) to be a compelling choice for this problem as it scales well with the number of points.

Randomized Iterative Algorithms for Fisher Discriminant Analysis

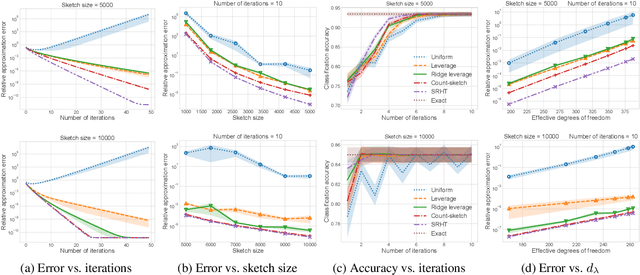
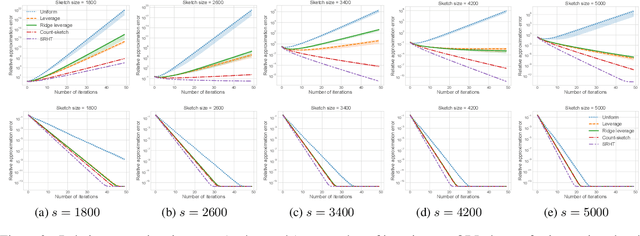
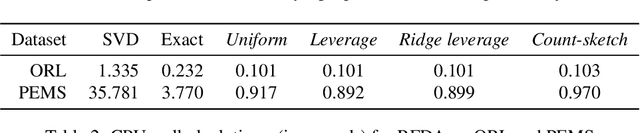
Fisher discriminant analysis (FDA) is a widely used method for classification and dimensionality reduction. When the number of predictor variables greatly exceeds the number of observations, one of the alternatives for conventional FDA is regularized Fisher discriminant analysis (RFDA). In this paper, we present a simple, iterative, sketching-based algorithm for RFDA that comes with provable accuracy guarantees when compared to the conventional approach. Our analysis builds upon two simple structural results that boil down to randomized matrix multiplication, a fundamental and well-understood primitive of randomized linear algebra. We analyze the behavior of RFDA when the ridge leverage and the standard leverage scores are used to select predictor variables and we prove that accurate approximations can be achieved by a sample whose size depends on the effective degrees of freedom of the RFDA problem. Our results yield significant improvements over existing approaches and our empirical evaluations support our theoretical analyses.

Structural Conditions for Projection-Cost Preservation via Randomized Matrix Multiplication

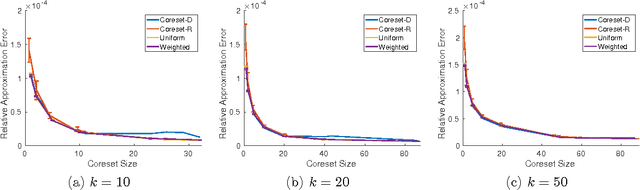
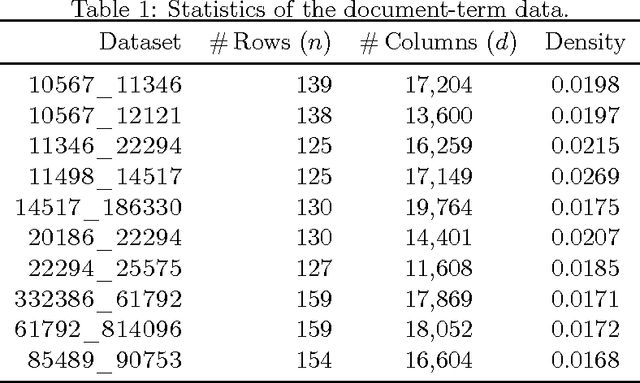
Projection-cost preservation is a low-rank approximation guarantee which ensures that the cost of any rank-$k$ projection can be preserved using a smaller sketch of the original data matrix. We present a general structural result outlining four sufficient conditions to achieve projection-cost preservation. These conditions can be satisfied using tools from the Randomized Linear Algebra literature.

Stochastic Gradient Descent for Relational Logistic Regression via Partial Network Crawls

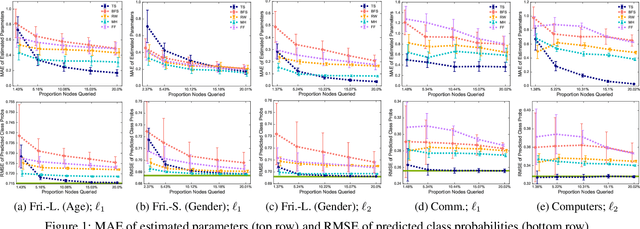
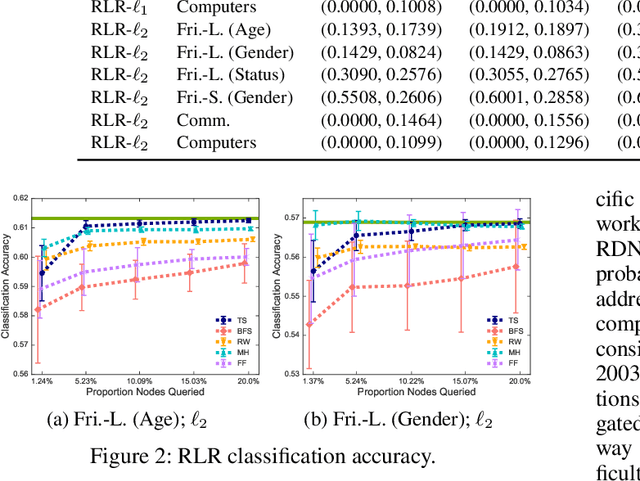
Research in statistical relational learning has produced a number of methods for learning relational models from large-scale network data. While these methods have been successfully applied in various domains, they have been developed under the unrealistic assumption of full data access. In practice, however, the data are often collected by crawling the network, due to proprietary access, limited resources, and privacy concerns. Recently, we showed that the parameter estimates for relational Bayes classifiers computed from network samples collected by existing network crawlers can be quite inaccurate, and developed a crawl-aware estimation method for such models (Yang, Ribeiro, and Neville, 2017). In this work, we extend the methodology to learning relational logistic regression models via stochastic gradient descent from partial network crawls, and show that the proposed method yields accurate parameter estimates and confidence intervals.