Optimization on the Surface of the -Sphere

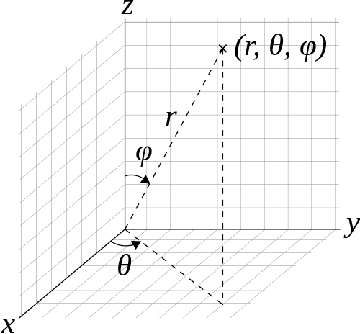
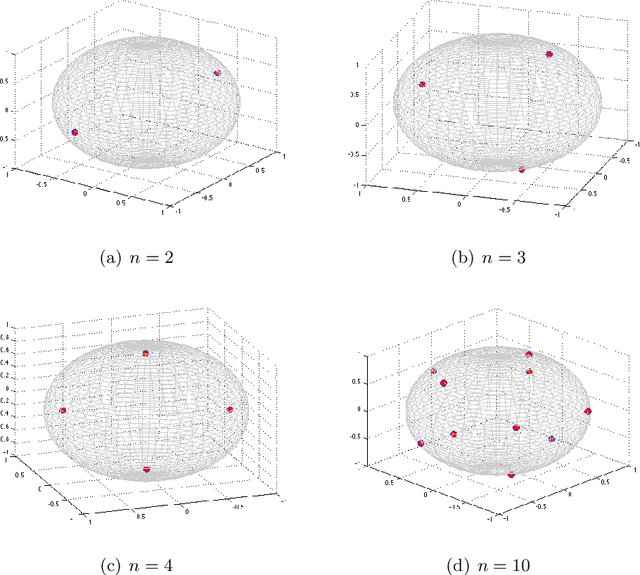
Thomson problem is a classical problem in physics to study how $n$ number of charged particles distribute themselves on the surface of a sphere of $k$ dimensions. When $k=2$, i.e. a 2-sphere (a circle), the particles appear at equally spaced points. Such a configuration can be computed analytically. However, for higher dimensions such as $k \ge 3$, i.e. the case of 3-sphere (standard sphere), there is not much that is understood analytically. Finding global minimum of the problem under these settings is particularly tough since the optimization problem becomes increasingly computationally intensive with larger values of $k$ and $n$. In this work, we explore a wide variety of numerical optimization methods to solve the Thomson problem. In our empirical study, we find stochastic gradient based methods (SGD) to be a compelling choice for this problem as it scales well with the number of points.