Agniva Chowdhury
SOCKET: SOft Collison Kernel EsTimator for Sparse Attention
Feb 06, 2026Abstract:Exploiting sparsity during long-context inference is central to scaling large language models, as attention dominates the cost of autoregressive decoding. Sparse attention reduces this cost by restricting computation to a subset of tokens, but its effectiveness depends critically on efficient scoring and selection of relevant tokens at inference time. We revisit Locality-Sensitive Hashing (LSH) as a sparsification primitive and introduce SOCKET, a SOft Collision Kernel EsTimator that replaces hard bucket matches with probabilistic, similarity-aware aggregation. Our key insight is that hard LSH produces discrete collision signals and is therefore poorly suited for ranking. In contrast, soft LSH aggregates graded collision evidence across hash tables, preserving the stability of relative ordering among the true top-$k$ tokens. This transformation elevates LSH from a candidate-generation heuristic to a principled and mathematically grounded scoring kernel for sparse attention. Leveraging this property, SOCKET enables efficient token selection without ad-hoc voting mechanism, and matches or surpasses established sparse attention baselines across multiple long-context benchmarks using diverse set of models. With a custom CUDA kernel for scoring keys and a Flash Decode Triton backend for sparse attention, SOCKET achieves up to 1.5$\times$ higher throughput than FlashAttention, making it an effective tool for long-context inference. Code is open-sourced at https://github.com/amarka8/SOCKET.
A Provably Accurate Randomized Sampling Algorithm for Logistic Regression
Feb 29, 2024


Abstract:In statistics and machine learning, logistic regression is a widely-used supervised learning technique primarily employed for binary classification tasks. When the number of observations greatly exceeds the number of predictor variables, we present a simple, randomized sampling-based algorithm for logistic regression problem that guarantees high-quality approximations to both the estimated probabilities and the overall discrepancy of the model. Our analysis builds upon two simple structural conditions that boil down to randomized matrix multiplication, a fundamental and well-understood primitive of randomized numerical linear algebra. We analyze the properties of estimated probabilities of logistic regression when leverage scores are used to sample observations, and prove that accurate approximations can be achieved with a sample whose size is much smaller than the total number of observations. To further validate our theoretical findings, we conduct comprehensive empirical evaluations. Overall, our work sheds light on the potential of using randomized sampling approaches to efficiently approximate the estimated probabilities in logistic regression, offering a practical and computationally efficient solution for large-scale datasets.
Deep Learning with Physics Priors as Generalized Regularizers
Dec 14, 2023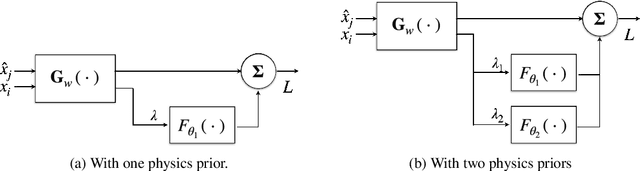
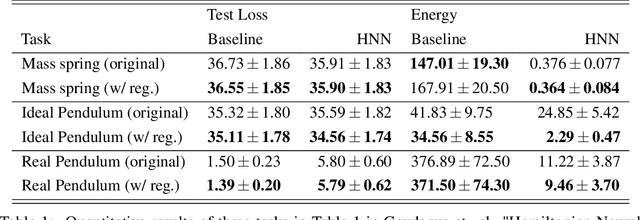
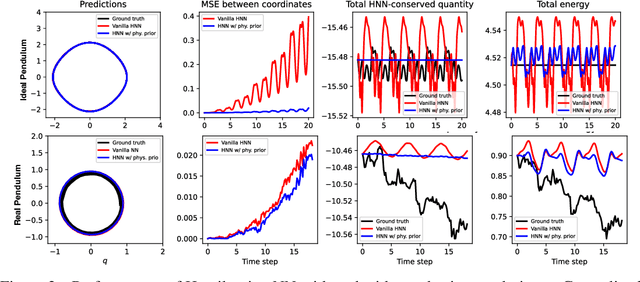

Abstract:In various scientific and engineering applications, there is typically an approximate model of the underlying complex system, even though it contains both aleatoric and epistemic uncertainties. In this paper, we present a principled method to incorporate these approximate models as physics priors in modeling, to prevent overfitting and enhancing the generalization capabilities of the trained models. Utilizing the structural risk minimization (SRM) inductive principle pioneered by Vapnik, this approach structures the physics priors into generalized regularizers. The experimental results demonstrate that our method achieves up to two orders of magnitude of improvement in testing accuracy.
Approximation Algorithms for Sparse Principal Component Analysis
Jun 23, 2020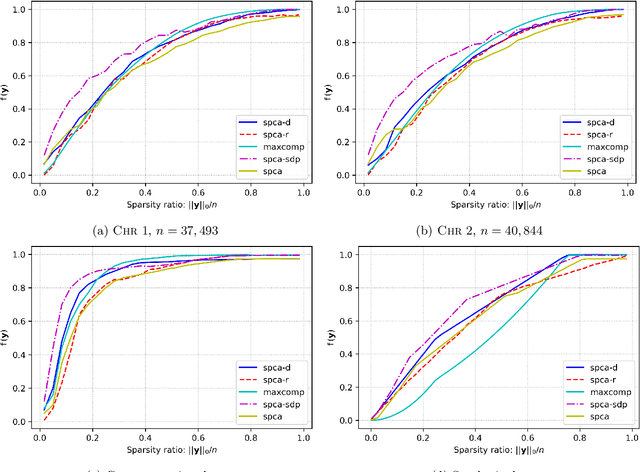
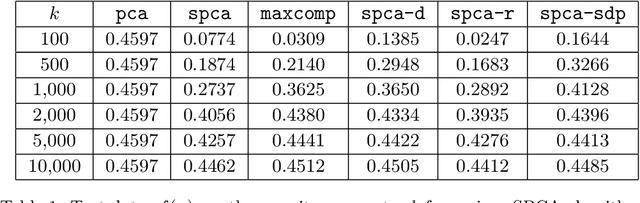
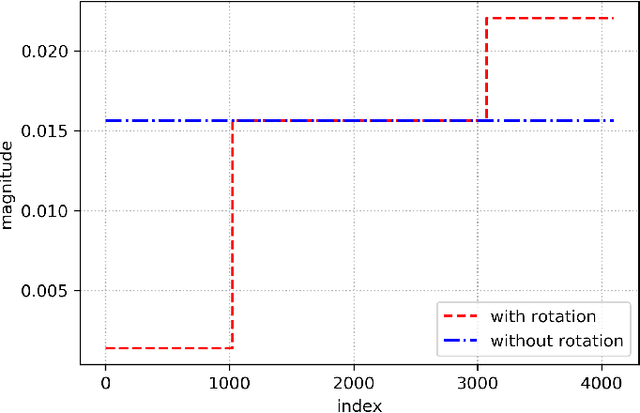
Abstract:We present three provably accurate, polynomial time, approximation algorithms for the Sparse Principal Component Analysis (SPCA) problem, without imposing any restrictive assumptions on the input covariance matrix. The first algorithm is based on randomized matrix multiplication; the second algorithm is based on a novel deterministic thresholding scheme; and the third algorithm is based on a semidefinite programming relaxation of SPCA. All algorithms come with provable guarantees and run in low-degree polynomial time. Our empirical evaluations confirm our theoretical findings.
Randomized Iterative Algorithms for Fisher Discriminant Analysis
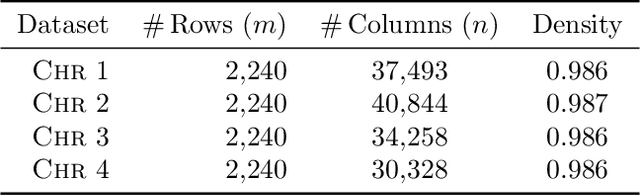
Sep 09, 2018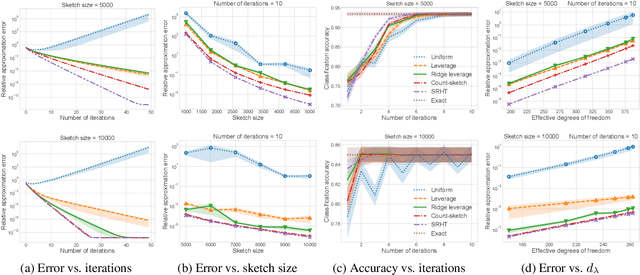

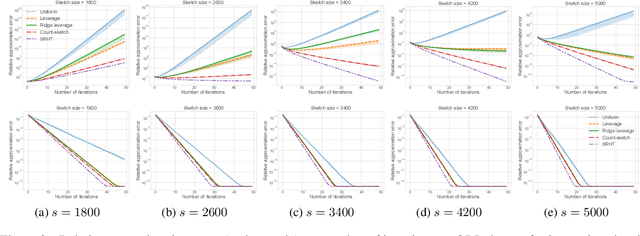
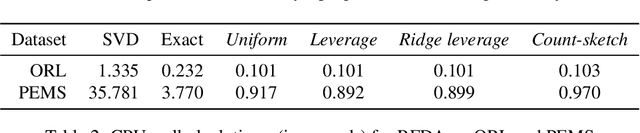
Abstract:Fisher discriminant analysis (FDA) is a widely used method for classification and dimensionality reduction. When the number of predictor variables greatly exceeds the number of observations, one of the alternatives for conventional FDA is regularized Fisher discriminant analysis (RFDA). In this paper, we present a simple, iterative, sketching-based algorithm for RFDA that comes with provable accuracy guarantees when compared to the conventional approach. Our analysis builds upon two simple structural results that boil down to randomized matrix multiplication, a fundamental and well-understood primitive of randomized linear algebra. We analyze the behavior of RFDA when the ridge leverage and the standard leverage scores are used to select predictor variables and we prove that accurate approximations can be achieved by a sample whose size depends on the effective degrees of freedom of the RFDA problem. Our results yield significant improvements over existing approaches and our empirical evaluations support our theoretical analyses.
Structural Conditions for Projection-Cost Preservation via Randomized Matrix Multiplication
Aug 17, 2018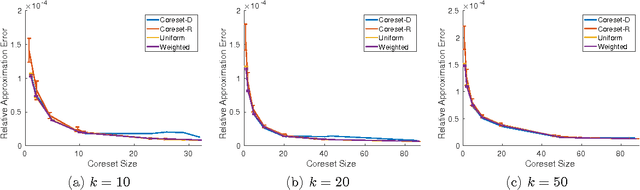
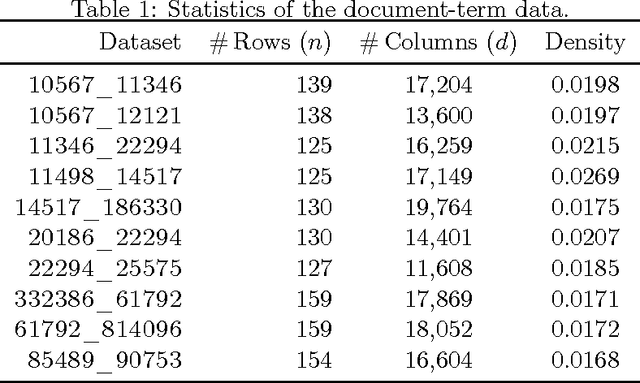


Abstract:Projection-cost preservation is a low-rank approximation guarantee which ensures that the cost of any rank-$k$ projection can be preserved using a smaller sketch of the original data matrix. We present a general structural result outlining four sufficient conditions to achieve projection-cost preservation. These conditions can be satisfied using tools from the Randomized Linear Algebra literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge