Results of the Big ANN: NeurIPS'23 competition

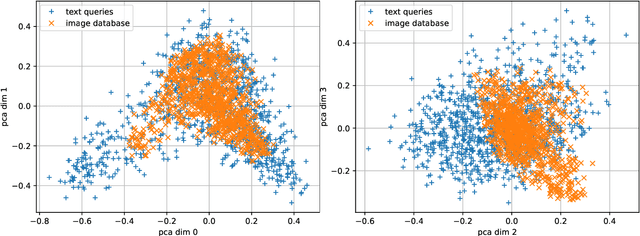
The 2023 Big ANN Challenge, held at NeurIPS 2023, focused on advancing the state-of-the-art in indexing data structures and search algorithms for practical variants of Approximate Nearest Neighbor (ANN) search that reflect the growing complexity and diversity of workloads. Unlike prior challenges that emphasized scaling up classical ANN search ~\cite{DBLP:conf/nips/SimhadriWADBBCH21}, this competition addressed filtered search, out-of-distribution data, sparse and streaming variants of ANNS. Participants developed and submitted innovative solutions that were evaluated on new standard datasets with constrained computational resources. The results showcased significant improvements in search accuracy and efficiency over industry-standard baselines, with notable contributions from both academic and industrial teams. This paper summarizes the competition tracks, datasets, evaluation metrics, and the innovative approaches of the top-performing submissions, providing insights into the current advancements and future directions in the field of approximate nearest neighbor search.

Do Counterfactual Examples Complicate Adversarial Training?

We leverage diffusion models to study the robustness-performance tradeoff of robust classifiers. Our approach introduces a simple, pretrained diffusion method to generate low-norm counterfactual examples (CEs): semantically altered data which results in different true class membership. We report that the confidence and accuracy of robust models on their clean training data are associated with the proximity of the data to their CEs. Moreover, robust models perform very poorly when evaluated on the CEs directly, as they become increasingly invariant to the low-norm, semantic changes brought by CEs. The results indicate a significant overlap between non-robust and semantic features, countering the common assumption that non-robust features are not interpretable.

Deep Learning with Physics Priors as Generalized Regularizers

In various scientific and engineering applications, there is typically an approximate model of the underlying complex system, even though it contains both aleatoric and epistemic uncertainties. In this paper, we present a principled method to incorporate these approximate models as physics priors in modeling, to prevent overfitting and enhancing the generalization capabilities of the trained models. Utilizing the structural risk minimization (SRM) inductive principle pioneered by Vapnik, this approach structures the physics priors into generalized regularizers. The experimental results demonstrate that our method achieves up to two orders of magnitude of improvement in testing accuracy.

Adversarial Estimation of Topological Dimension with Harmonic Score Maps

Quantification of the number of variables needed to locally explain complex data is often the first step to better understanding it. Existing techniques from intrinsic dimension estimation leverage statistical models to glean this information from samples within a neighborhood. However, existing methods often rely on well-picked hyperparameters and ample data as manifold dimension and curvature increases. Leveraging insight into the fixed point of the score matching objective as the score map is regularized by its Dirichlet energy, we show that it is possible to retrieve the topological dimension of the manifold learned by the score map. We then introduce a novel method to measure the learned manifold's topological dimension (i.e., local intrinsic dimension) using adversarial attacks, thereby generating useful interpretations of the learned manifold.

Semi-Supervised Learning of Dynamical Systems with Neural Ordinary Differential Equations: A Teacher-Student Model Approach

Modeling dynamical systems is crucial for a wide range of tasks, but it remains challenging due to complex nonlinear dynamics, limited observations, or lack of prior knowledge. Recently, data-driven approaches such as Neural Ordinary Differential Equations (NODE) have shown promising results by leveraging the expressive power of neural networks to model unknown dynamics. However, these approaches often suffer from limited labeled training data, leading to poor generalization and suboptimal predictions. On the other hand, semi-supervised algorithms can utilize abundant unlabeled data and have demonstrated good performance in classification and regression tasks. We propose TS-NODE, the first semi-supervised approach to modeling dynamical systems with NODE. TS-NODE explores cheaply generated synthetic pseudo rollouts to broaden exploration in the state space and to tackle the challenges brought by lack of ground-truth system data under a teacher-student model. TS-NODE employs an unified optimization framework that corrects the teacher model based on the student's feedback while mitigating the potential false system dynamics present in pseudo rollouts. TS-NODE demonstrates significant performance improvements over a baseline Neural ODE model on multiple dynamical system modeling tasks.

Extreme Risk Mitigation in Reinforcement Learning using Extreme Value Theory

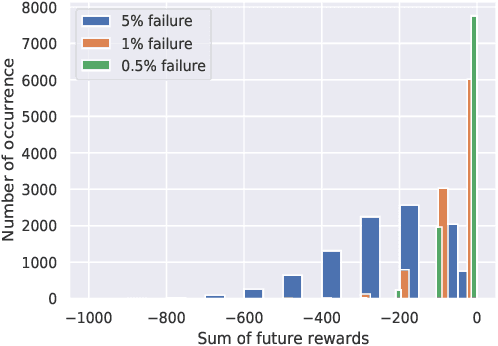
Risk-sensitive reinforcement learning (RL) has garnered significant attention in recent years due to the growing interest in deploying RL agents in real-world scenarios. A critical aspect of risk awareness involves modeling highly rare risk events (rewards) that could potentially lead to catastrophic outcomes. These infrequent occurrences present a formidable challenge for data-driven methods aiming to capture such risky events accurately. While risk-aware RL techniques do exist, their level of risk aversion heavily relies on the precision of the state-action value function estimation when modeling these rare occurrences. Our work proposes to enhance the resilience of RL agents when faced with very rare and risky events by focusing on refining the predictions of the extreme values predicted by the state-action value function distribution. To achieve this, we formulate the extreme values of the state-action value function distribution as parameterized distributions, drawing inspiration from the principles of extreme value theory (EVT). This approach effectively addresses the issue of infrequent occurrence by leveraging EVT-based parameterization. Importantly, we theoretically demonstrate the advantages of employing these parameterized distributions in contrast to other risk-averse algorithms. Our evaluations show that the proposed method outperforms other risk averse RL algorithms on a diverse range of benchmark tasks, each encompassing distinct risk scenarios.

Disentangling Learning Representations with Density Estimation

Disentangled learning representations have promising utility in many applications, but they currently suffer from serious reliability issues. We present Gaussian Channel Autoencoder (GCAE), a method which achieves reliable disentanglement via flexible density estimation of the latent space. GCAE avoids the curse of dimensionality of density estimation by disentangling subsets of its latent space with the Dual Total Correlation (DTC) metric, thereby representing its high-dimensional latent joint distribution as a collection of many low-dimensional conditional distributions. In our experiments, GCAE achieves highly competitive and reliable disentanglement scores compared with state-of-the-art baselines.

NashAE: Disentangling Representations through Adversarial Covariance Minimization

We present a self-supervised method to disentangle factors of variation in high-dimensional data that does not rely on prior knowledge of the underlying variation profile (e.g., no assumptions on the number or distribution of the individual latent variables to be extracted). In this method which we call NashAE, high-dimensional feature disentanglement is accomplished in the low-dimensional latent space of a standard autoencoder (AE) by promoting the discrepancy between each encoding element and information of the element recovered from all other encoding elements. Disentanglement is promoted efficiently by framing this as a minmax game between the AE and an ensemble of regression networks which each provide an estimate of an element conditioned on an observation of all other elements. We quantitatively compare our approach with leading disentanglement methods using existing disentanglement metrics. Furthermore, we show that NashAE has increased reliability and increased capacity to capture salient data characteristics in the learned latent representation.

Gradient-based Novelty Detection Boosted by Self-supervised Binary Classification

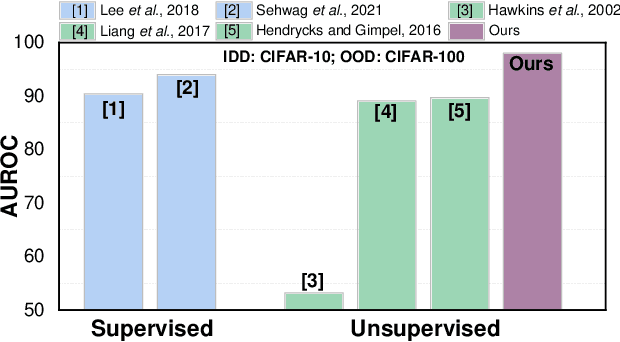
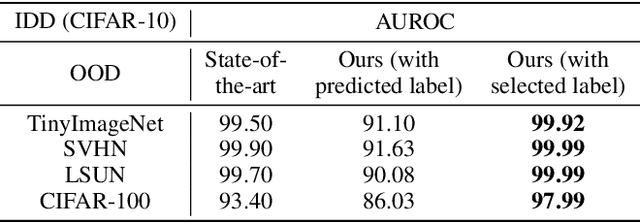
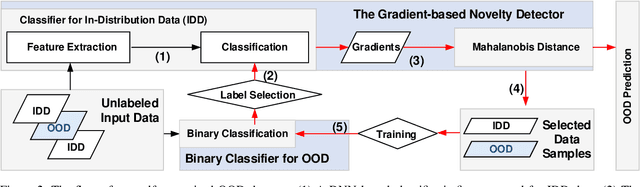
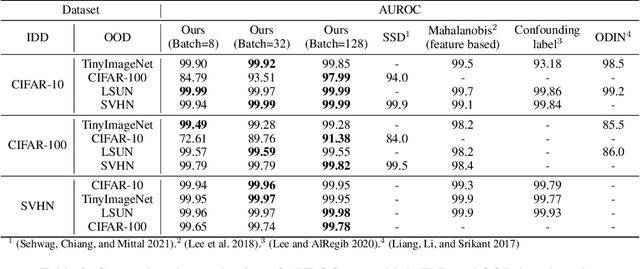
Novelty detection aims to automatically identify out-of-distribution (OOD) data, without any prior knowledge of them. It is a critical step in data monitoring, behavior analysis and other applications, helping enable continual learning in the field. Conventional methods of OOD detection perform multi-variate analysis on an ensemble of data or features, and usually resort to the supervision with OOD data to improve the accuracy. In reality, such supervision is impractical as one cannot anticipate the anomalous data. In this paper, we propose a novel, self-supervised approach that does not rely on any pre-defined OOD data: (1) The new method evaluates the Mahalanobis distance of the gradients between the in-distribution and OOD data. (2) It is assisted by a self-supervised binary classifier to guide the label selection to generate the gradients, and maximize the Mahalanobis distance. In the evaluation with multiple datasets, such as CIFAR-10, CIFAR-100, SVHN and TinyImageNet, the proposed approach consistently outperforms state-of-the-art supervised and unsupervised methods in the area under the receiver operating characteristic (AUROC) and area under the precision-recall curve (AUPR) metrics. We further demonstrate that this detector is able to accurately learn one OOD class in continual learning.

On the Stochastic Stability of Deep Markov Models

Deep Markov models (DMM) are generative models that are scalable and expressive generalization of Markov models for representation, learning, and inference problems. However, the fundamental stochastic stability guarantees of such models have not been thoroughly investigated. In this paper, we provide sufficient conditions of DMM's stochastic stability as defined in the context of dynamical systems and propose a stability analysis method based on the contraction of probabilistic maps modeled by deep neural networks. We make connections between the spectral properties of neural network's weights and different types of used activation functions on the stability and overall dynamic behavior of DMMs with Gaussian distributions. Based on the theory, we propose a few practical methods for designing constrained DMMs with guaranteed stability. We empirically substantiate our theoretical results via intuitive numerical experiments using the proposed stability constraints.