Do Counterfactual Examples Complicate Adversarial Training?

We leverage diffusion models to study the robustness-performance tradeoff of robust classifiers. Our approach introduces a simple, pretrained diffusion method to generate low-norm counterfactual examples (CEs): semantically altered data which results in different true class membership. We report that the confidence and accuracy of robust models on their clean training data are associated with the proximity of the data to their CEs. Moreover, robust models perform very poorly when evaluated on the CEs directly, as they become increasingly invariant to the low-norm, semantic changes brought by CEs. The results indicate a significant overlap between non-robust and semantic features, countering the common assumption that non-robust features are not interpretable.

Min-K%++: Improved Baseline for Detecting Pre-Training Data from Large Language Models

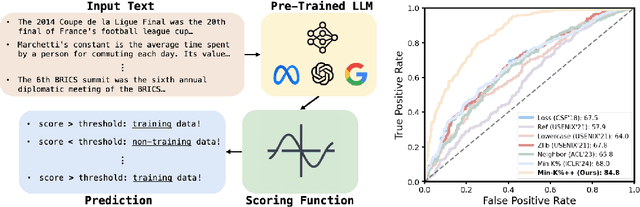
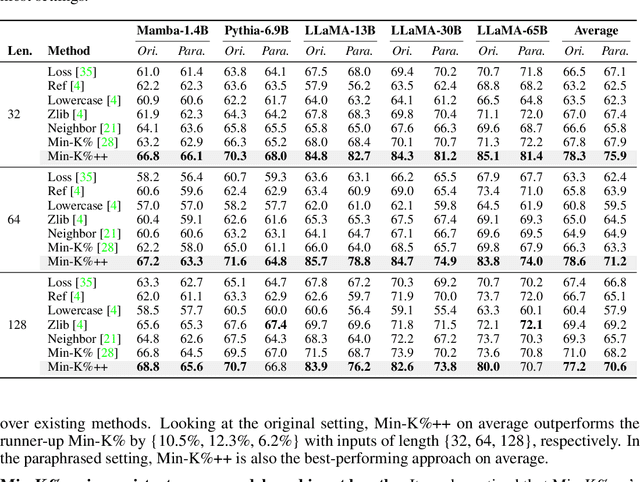
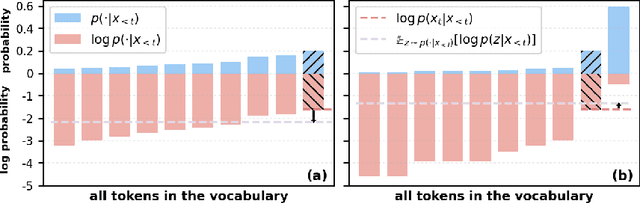
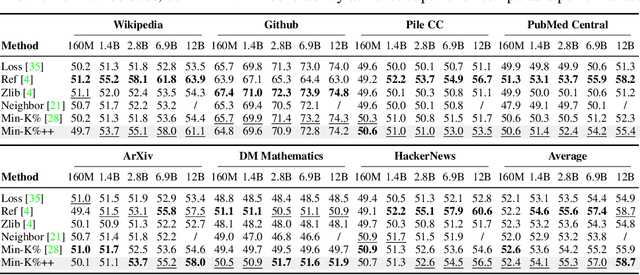
The problem of pre-training data detection for large language models (LLMs) has received growing attention due to its implications in critical issues like copyright violation and test data contamination. The current state-of-the-art approach, Min-K%, measures the raw token probability which we argue may not be the most informative signal. Instead, we propose Min-K%++ to normalize the token probability with statistics of the categorical distribution over the whole vocabulary, which accurately reflects the relative likelihood of the target token compared with other candidate tokens in the vocabulary. Theoretically, we back up our method by showing that the statistic it estimates is explicitly optimized during LLM training, thus serving as a reliable indicator for detecting training data. Empirically, on the WikiMIA benchmark, Min-K%++ outperforms the SOTA Min-K% by 6.2% to 10.5% in detection AUROC averaged over five models. On the more challenging MIMIR benchmark, Min-K%++ consistently improves upon Min-K% and performs on par with reference-based method, despite not requiring an extra reference model.

Adversarial Estimation of Topological Dimension with Harmonic Score Maps

Quantification of the number of variables needed to locally explain complex data is often the first step to better understanding it. Existing techniques from intrinsic dimension estimation leverage statistical models to glean this information from samples within a neighborhood. However, existing methods often rely on well-picked hyperparameters and ample data as manifold dimension and curvature increases. Leveraging insight into the fixed point of the score matching objective as the score map is regularized by its Dirichlet energy, we show that it is possible to retrieve the topological dimension of the manifold learned by the score map. We then introduce a novel method to measure the learned manifold's topological dimension (i.e., local intrinsic dimension) using adversarial attacks, thereby generating useful interpretations of the learned manifold.

Disentangling Learning Representations with Density Estimation

Disentangled learning representations have promising utility in many applications, but they currently suffer from serious reliability issues. We present Gaussian Channel Autoencoder (GCAE), a method which achieves reliable disentanglement via flexible density estimation of the latent space. GCAE avoids the curse of dimensionality of density estimation by disentangling subsets of its latent space with the Dual Total Correlation (DTC) metric, thereby representing its high-dimensional latent joint distribution as a collection of many low-dimensional conditional distributions. In our experiments, GCAE achieves highly competitive and reliable disentanglement scores compared with state-of-the-art baselines.

NashAE: Disentangling Representations through Adversarial Covariance Minimization

We present a self-supervised method to disentangle factors of variation in high-dimensional data that does not rely on prior knowledge of the underlying variation profile (e.g., no assumptions on the number or distribution of the individual latent variables to be extracted). In this method which we call NashAE, high-dimensional feature disentanglement is accomplished in the low-dimensional latent space of a standard autoencoder (AE) by promoting the discrepancy between each encoding element and information of the element recovered from all other encoding elements. Disentanglement is promoted efficiently by framing this as a minmax game between the AE and an ensemble of regression networks which each provide an estimate of an element conditioned on an observation of all other elements. We quantitatively compare our approach with leading disentanglement methods using existing disentanglement metrics. Furthermore, we show that NashAE has increased reliability and increased capacity to capture salient data characteristics in the learned latent representation.