NashAE: Disentangling Representations through Adversarial Covariance Minimization

We present a self-supervised method to disentangle factors of variation in high-dimensional data that does not rely on prior knowledge of the underlying variation profile (e.g., no assumptions on the number or distribution of the individual latent variables to be extracted). In this method which we call NashAE, high-dimensional feature disentanglement is accomplished in the low-dimensional latent space of a standard autoencoder (AE) by promoting the discrepancy between each encoding element and information of the element recovered from all other encoding elements. Disentanglement is promoted efficiently by framing this as a minmax game between the AE and an ensemble of regression networks which each provide an estimate of an element conditioned on an observation of all other elements. We quantitatively compare our approach with leading disentanglement methods using existing disentanglement metrics. Furthermore, we show that NashAE has increased reliability and increased capacity to capture salient data characteristics in the learned latent representation.

Challenges in Bayesian inference via Markov chain Monte Carlo for neural networks

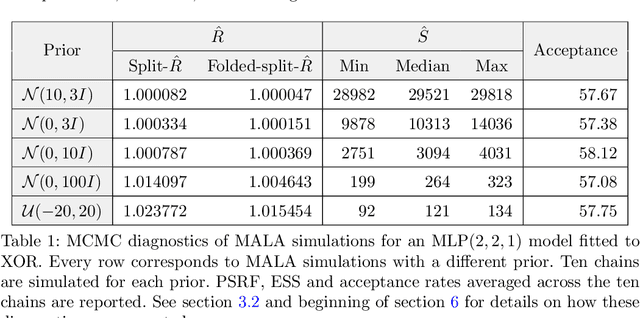
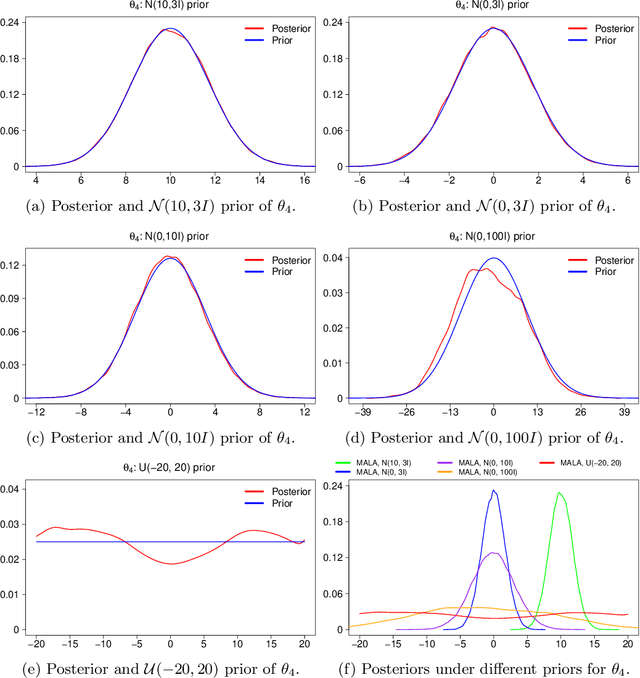
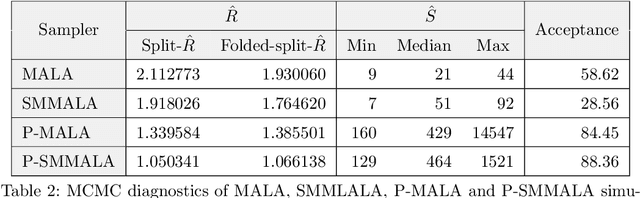
Markov chain Monte Carlo (MCMC) methods and neural networks are instrumental in tackling inferential and prediction problems. However, Bayesian inference based on joint use of MCMC methods and of neural networks is limited. This paper reviews the main challenges posed by neural networks to MCMC developments, including lack of parameter identifiability due to weight symmetries, prior specification effects, and consequently high computational cost and convergence failure. Population and manifold MCMC algorithms are combined to demonstrate these challenges via multilayer perceptron (MLP) examples and to develop case studies for assessing the capacity of approximate inference methods to uncover the posterior covariance of neural network parameters. Some of these challenges, such as high computational cost arising from the application of neural networks to big data and parameter identifiability arising from weight symmetries, stimulate research towards more scalable approximate MCMC methods or towards MCMC methods in reduced parameter spaces.