Challenges in Bayesian inference via Markov chain Monte Carlo for neural networks

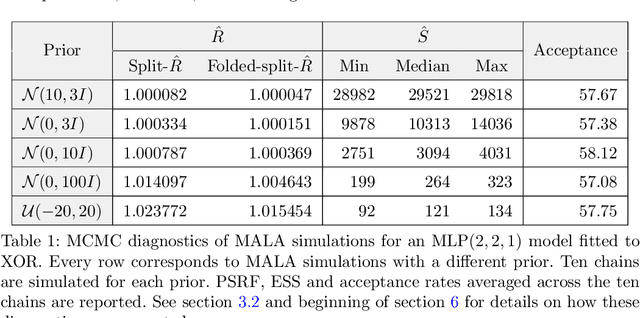
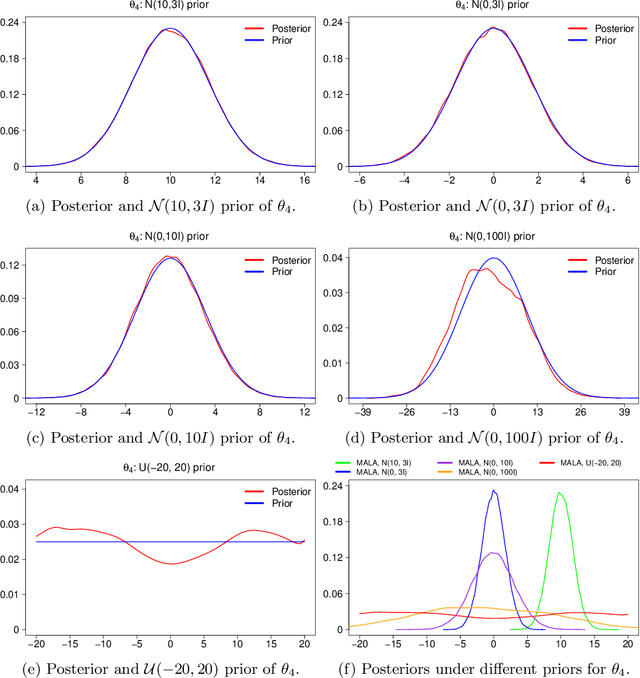
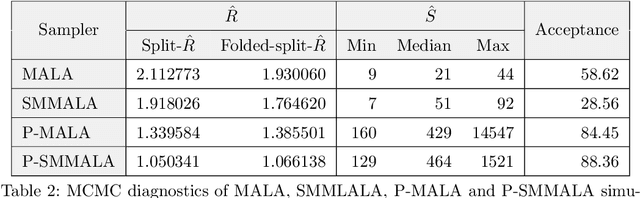
Markov chain Monte Carlo (MCMC) methods and neural networks are instrumental in tackling inferential and prediction problems. However, Bayesian inference based on joint use of MCMC methods and of neural networks is limited. This paper reviews the main challenges posed by neural networks to MCMC developments, including lack of parameter identifiability due to weight symmetries, prior specification effects, and consequently high computational cost and convergence failure. Population and manifold MCMC algorithms are combined to demonstrate these challenges via multilayer perceptron (MLP) examples and to develop case studies for assessing the capacity of approximate inference methods to uncover the posterior covariance of neural network parameters. Some of these challenges, such as high computational cost arising from the application of neural networks to big data and parameter identifiability arising from weight symmetries, stimulate research towards more scalable approximate MCMC methods or towards MCMC methods in reduced parameter spaces.